11 The Riemann Solver of Roe

注：
本文翻译自Riemann Solvers and Numerical Methods for Fluid Dynamics一书。

The Riemann Solver of Roe

1. Bases of the Roe Approach

m维双曲守恒定律

1.1 The Exact Riemann Problem and the Godunov Flux

Initial Boundary Value Problem:

\[\text{PDES: } \mathbf{U}_{t} + \mathbf{F}(\mathbf{U})_{x} = 0 \\ \text{ICs: } \mathbf{U}(x,0) = \mathbf{U}^{(0)}(x) \\ \text{BCs: } \mathbf{U}(0,t) = \mathbf{U}_{l}(t); \quad \mathbf{U}(L,t) = \mathbf{U}_{r}(t); \label{IBVP} \]

使用显示的守恒格式：

\[\mathbf{U}_{i}^{n+1} = \mathbf{U}_{i}^{n} + \frac{\Delta t}{\Delta x}[\mathbf{F}_{i-\frac{1}{2}} - \mathbf{F}_{i+\frac{1}{2}}] \]

假设\(\eqref{IBVP}\) 有解。在第六章中Godunov面通量被定义为：

\[\mathbf{F}_{i+\frac{1}{2}} = \mathbf{F}(\mathbf{U}_{i+\frac{1}{2}}(0)) \]

其中\(\mathbf{U}_{i+\frac{1}{2}}(0)\) 是黎曼问题

\[\mathbf{U}_{t} + \mathbf{F}(\mathbf{U})_{x} = 0 \\ \mathbf{U}(x,0) = \left\{\begin{matrix} \mathbf{U}_{L} & \text{if } x < 0 \\ \mathbf{U}_{R} & \text{if } x > 0 \end{matrix}\right. \label{riemann} \]

的在\(x/t\)位置处的相似解析解\(\mathbf{U}_{i+\frac{1}{2}}(x/t)\) 。

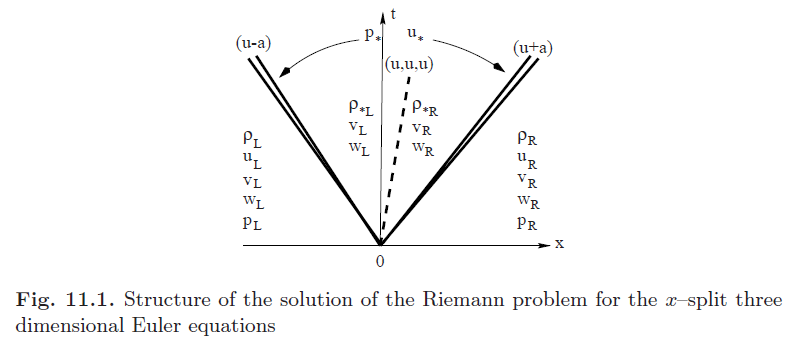
图11.1展示了在x方向分解的欧拉方程的解的结构，其中守恒量和通量向量为：

\[\mathbf{U} = \begin{bmatrix} \rho \\ \rho u \\ \rho v \\ \rho w \\ E \end{bmatrix} \qquad \mathbf{U} = \begin{bmatrix} \rho u \\ \rho u^2 + p \\ \rho uv \\ \rho uw \\ u(E+p) \end{bmatrix} \]

左波和右波中间的星号区域包含了问题的未知数。其中\(x/t = 0\) 代表时间轴，在Godunov格式中使用这些量。初始时刻的分段常量为：

\[\mathbf{W}_{L} = \begin{bmatrix} \rho_{L} \\ u_{L} \\ v_{L} \\ w_{L} \\ p_{L} \end{bmatrix} \qquad \mathbf{W}_{R} = \begin{bmatrix} \rho_{R} \\ u_{R} \\ v_{R} \\ w_{R} \\ p_{R} \end{bmatrix} \]

在Roe格式中直接近似通量函数\(\mathbf{F}_{i+\frac{1}{2}}\)

1.2 Approximate Conservation Laws

Roe直接近似求解黎曼问题\(\eqref{riemann}\)。引入Jacobian 矩阵：

\[\mathbf{A(\mathbf{U})} = \frac{\partial \mathbf{F}}{\partial \mathbf{U}} \]

对守恒方程\(\mathbf{U}_{t} + \mathbf{F}(\mathbf{U})_{x} = 0\) 链式求导可得：

\[\mathbf{U}_{t} + \mathbf{A(\mathbf{U})} \mathbf{U}_{x} = 0 \]

Roe把Jacobian矩阵替换为一个常系数Jacobian矩阵：

\[\tilde{\mathbf{A}} = \tilde{\mathbf{A}}(\mathbf{U}_{L}, \mathbf{U}_{R}) \]

把原始的PDE转化为：

\[\mathbf{U}_{t} + \tilde{\mathbf{A}} \mathbf{U}_{x} = 0 \]

原来的初值问题转化为：

\[\mathbf{U}_{t} + \tilde{\mathbf{A}} \mathbf{U}_{x} = 0 \\ \mathbf{U}(x,0) = \left\{\begin{matrix} \mathbf{U}_{L} & \text{if } x < 0 \\ \mathbf{U}_{R} & \text{if } x > 0 \end{matrix}\right. \]

然后求解析解。把原始的非线性的系统用线性的常系数系统近似，但是初始时刻的值不变。

对于大多双曲守恒律系统来说，Roe Jacobian 矩阵需要满足一下条件：

1. 系统的双曲性

\(\tilde{\mathbf{A}}\) 要有实特征值\(\tilde{\lambda}_{i} = \tilde{\lambda}_{i} (\mathbf{U}_{L}, \mathbf{U}_{L})\)，并且按照以下方式排列：

\[\tilde{\lambda}_{1} < \tilde{\lambda}_{i} < ... < \tilde{\lambda}_{m} \]

相应的右特征向量为：

\[\tilde{\mathbf{K}}^{(1)} , \tilde{\mathbf{K}}^{(2)}, ... \tilde{\mathbf{K}}^{(m)} \]

2. 与原始的矩阵一致：

   \[\tilde{\mathbf{A}}(\mathbf{U}, \mathbf{U}) = \mathbf{A}(\mathbf{U}) \]

3. 在间断处守恒：

   \[\mathbf{F}(\mathbf{U}_R) - \mathbf{F}(\mathbf{U}_L) = \tilde{\mathbf{A}}(\mathbf{U}_R - \mathbf{U}_L) \label{Conservation} \]

性质3能够保证精确捕捉激波。但是这并不代表在Godunov方法中，通过Roe近似格式求数值通量能够得到间断的解析解。

但是构造满足以上三个条件的双曲系统很复杂。但是对于理想气体的欧拉方程，Roe and Pike提出来了一些更简单的方法。

1.3 The Approximate Riemann Problem and the Intercell Flux

当得到了矩阵\(\tilde{\mathbf{A}}(\mathbf{U}_{L}, \mathbf{U}_{R})\) 及其特征值 \(\tilde{\lambda} (\mathbf{U}_{L}, \mathbf{U}_{R})\)和其右特征向量\(\tilde{\mathbf{K}}(\mathbf{U}_{L}, \mathbf{U}_{R})\)后，黎曼问题就可以通过2.3节、5.4节中的方法求解。通过把数据差异 \(\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L\) 写成右特征向量：

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L = \sum_{i=1}^{m} \tilde{\alpha}_{i}\tilde{\mathbf{K}}^{(i)} \]

需要得到波强度\(\tilde{\alpha}_{i} = \tilde{\alpha}_{i}(\mathbf{A}(\mathbf{U}_{L}, \mathbf{U}_{R})\)。此时沿着时间轴 \(x/t=0\) 的解\(\mathbf{U}_{i+\frac{1}{2}}(x/t)\) 为：

\[\mathbf{U}_{i+\frac{1}{2}}(0) = \mathbf{U}_L + \sum_{\tilde{\lambda}_i \le 0} \tilde{\alpha}_{i}\tilde{\mathbf{K}}^{(i)} \label{mid_u} \]

或者：

\[\mathbf{U}_{i+\frac{1}{2}}(0) = \mathbf{U}_R - \sum_{\tilde{\lambda}_i \ge 0} \tilde{\alpha}_{i}\tilde{\mathbf{K}}^{(i)} \label{mid_u1} \]

这样就能得到相应的数值通量。上述过程可看做修改后的守恒方程：

\[\bar{\mathbf{U}}_t = \bar{\mathbf{F}}(\bar{\mathbf{U}})_x = 0 \label{MDC} \]

通量为：

\[\overline{\mathbf{F}}(\overline{\mathbf{U}}) = \tilde{\mathbf{A}} \overline{\mathbf{U}} \]

相应的数值通量：

\[\mathbf{F}_{i+\frac{1}{2}} = \tilde{\mathbf{A}} \overline{\mathbf{U}}_{i+\frac{1}{2}}(0) \]

这个通量在右侧流速为超音速的时候会明显是不对的。因为此时算出来的通量\(\mathbf{F}_{i+\frac{1}{2}} \neq \mathbf{F}_L\)。正确的通量可以用以下任何一种积分形式计算：

\[\mathbf{F}_{0L} = \mathbf{F}_{L}- \mathbf{S}_{L} \mathbf{U}_{L} - \frac{1}{T}\int_{TS_L} ^{0} \mathbf{U}(x,T)dx \]

或者

\[\mathbf{F}_{0R} = \mathbf{F}_{R}- \mathbf{S}_{R} \mathbf{U}_{R} - \frac{1}{T}\int_{TS_R} ^{0} \mathbf{U}(x,T)dx \]

上面两个式子在10.2节中有具体的推导。其中，\(S_L, S_R\)分别为黎曼解析解中最快和最慢的波速。\(T\)是正的时间。如果\(\mathbf{U}(x,t)\)通过近似解求得，则\(\mathbf{F}_{0L}\)和\(\mathbf{F}_{0L}\)要满足一致性（Consistency Condition，Sect. 10.2 of Chap. 10.）。

如果\(\overline{\mathbf{U}}_{i+\frac{1}{2}}(x, t)\)是修改后的守恒方程\(\eqref{MDC}\)的解，上述两式的积分部分可转化为：

\[\int_{TS_L} ^{0} \overline{\mathbf{U}}_{i+\frac{1}{2}}(x,T)dx = T[\overline{\mathbf{F}}(\mathbf{U}_L) - \overline{\mathbf{F}}(\overline{\mathbf{U}}_{i+\frac{1}{2}}(0))] - TS_L\mathbf{U}_L \]

和

\[\int_{0}^{TS_R} \overline{\mathbf{U}}_{i+\frac{1}{2}}(x,T)dx = T[\overline{\mathbf{F}}(\overline{\mathbf{U}}_{i+\frac{1}{2}}(0)) - \overline{\mathbf{F}}(\mathbf{U}_R)] - TS_L\mathbf{U}_L \]

带入后可得：

\[\mathbf{F}_{0L} = \overline{\mathbf{F}}(\overline{\mathbf{U}}_{i+\frac{1}{2}}(0)) + \mathbf{F}(\mathbf{U}_{L}) - \overline{\mathbf{F}}(\mathbf{U}_L) \]

或者：

\[\mathbf{F}_{0R} = \overline{\mathbf{F}}(\overline{\mathbf{U}}_{i+\frac{1}{2}}(0)) + \mathbf{F}(\mathbf{U}_{R}) - \overline{\mathbf{F}}(\mathbf{U}_R) \]

其中\(\overline{\mathbf{U}}_{i+\frac{1}{2}}(0)\)由\(\eqref{mid_u}\)和\(\eqref{mid_u1}\)计算，通量\(\overline{\mathbf{F}} = \tilde{\mathbf{A}} \overline{\mathbf{U}}\)，得到：

\[\mathbf{F}_{i+\frac{1}{2}} = \mathbf{F}_{L} + \sum_{\tilde{\lambda}_i \le 0} \tilde{\alpha}_{i} \tilde{\lambda}_i \tilde{\mathbf{K}}^{(i)} \]

或者：

\[\mathbf{F}_{i+\frac{1}{2}} = \mathbf{F}_{R} - \sum_{\tilde{\lambda}_i \ge 0} \tilde{\alpha}_{i} \tilde{\lambda}_i \tilde{\mathbf{K}}^{(i)} \]

或者写为：

\[\mathbf{F}_{i+\frac{1}{2}} = \frac{1}{2} (\mathbf{F}_{L} + \mathbf{F}_{R}) - \frac{1}{2} (\sum_{i=1} ^{m} \tilde{\alpha}_{i} |\tilde{\lambda}_i| \tilde{\mathbf{K}}^{(i)}) \label{Roe_flux} \]

2. The Original Roe Method

为了计算\(\eqref{Roe_flux}\) 需要得到平均特征值\(\tilde{\lambda}_i\)，对应的右特征值\(\tilde{\mathbf{K}}^{(i)}\)，和波强度\(\tilde{\alpha}_{i}\)。在Roe原始论文中，先得到平均矩阵\(\tilde{\mathbf{A}}\)，然后得到右特征值\(\tilde{\mathbf{K}}^{(i)}\)，和波强度\(\tilde{\alpha}_{i}\)。构造矩阵，要满足上述三个条件，前两个好满足，后面一个不好满足。这种方式缺陷很多，比如：矩阵不唯一，得到的格式复杂。

突破：通过引入参数向量\(\mathbf{Q}\)构造\(\tilde{\mathbf{A}}\)，这样守恒量向量\(\mathbf{U}\)和通量向量\(\mathbf{F}(\mathbf{U})\)能够通过\(\mathbf{Q}\)表示：

\[\mathbf{U} = \mathbf{U}(\mathbf{Q}) \quad \mathbf{F} = \mathbf{F}(\mathbf{Q}) \]

两个很重要的步骤：

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L, \quad \Delta\mathbf{F} = \mathbf{F} (\mathbf{U}_R) - \mathbf{F} (\mathbf{U}_L) \label{jump} \]

可以通过\(\Delta \mathbf{Q} = \mathbf{Q}_R - \mathbf{Q}_L\)表示。然后均值通过对\(\mathbf{Q}\) 代数平均得到。

2.1 The Isothermal Equations

isothermal equations：

\[\mathbf{U}_{t} + \mathbf{F}(\mathbf{U})_{x} = 0 \\ \mathbf{U} \equiv \begin{bmatrix}u_1 \\ u_2 \end{bmatrix}\equiv \begin{bmatrix}\rho \\ \rho u \end{bmatrix} , \quad \mathbf{F} \equiv \begin{bmatrix}f_1 \\ f_2 \end{bmatrix}\equiv \begin{bmatrix}\rho u \\ \rho u^2 + a^2\rho \end{bmatrix} \]

其中：

\[\mathbf{A(\mathbf{U})} = \begin{bmatrix} 0 & 1 \\ a^2-u^2 & 2u \end{bmatrix} \\ \lambda_1 = u - a, \quad \lambda_2 = u + a \\ \mathbf{K}^{(1)} = \begin{bmatrix} 1 \\ u-a \end{bmatrix}, \quad \mathbf{K}^{(2)} = \begin{bmatrix} 1 \\ u+a \end{bmatrix} \]

选择参数矩阵：

\[\mathbf{Q} \equiv \begin{bmatrix} q_1 \\ q_2 \end{bmatrix} \equiv \frac{\mathbf{U}}{\sqrt{\rho}} = \begin{bmatrix} \sqrt{\rho} \\ \sqrt{\rho} u \end{bmatrix}： \]

表示成\(\mathbf{Q}\)的形式

\[\mathbf{U} \equiv \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}\equiv q_1\mathbf{Q} = \begin{bmatrix} q_1^2 \\ q_1 q_2 \end{bmatrix} \]

且：

\[\mathbf{F} \equiv \begin{bmatrix}f_1 \\ f_2 \end{bmatrix} = \begin{bmatrix}q_1q_2 \\ q_2^2+a^2q_1^2 \end{bmatrix} \]

定义平均向量\(\tilde{\mathbf{Q}} = (\tilde{q}_1, \tilde{q}_2)^T\)。通过简单的代数平均：

\[\tilde{\mathbf{Q}} = \begin{bmatrix} \tilde q_1 \\ \tilde q_2 \end{bmatrix} = \frac{1}{2}(\mathbf{Q}_L+\mathbf{Q}_R) = \frac{1}{2}\begin{bmatrix} \sqrt{\rho_L} + \sqrt{\rho_R} \\ \sqrt{\rho_L}u_L + \sqrt{\rho_R}u_R \end{bmatrix} \]

由此可以得到\(\tilde{\mathbf{B}} = \tilde{\mathbf{B}}(\tilde{\mathbf{Q}})\) 和\(\tilde{\mathbf{C}} = \tilde{\mathbf{C}}(\tilde{\mathbf{Q}})\), 式\(\eqref{jump}\)中的跳跃\(\Delta \mathbf{U}\)和\(\Delta \mathbf{F}\)可以表示为：

\[\Delta \mathbf{U} = \tilde{\mathbf{B}}\Delta \mathbf{Q}, \quad \Delta \mathbf{F} = \tilde{\mathbf{C}}\Delta \mathbf{Q} \label{jump_q} \]

以上公式可得：

\[\quad \Delta \mathbf{F} = (\tilde{\mathbf{C}}\tilde{\mathbf{B}}^{-1}) \Delta \mathbf{U} \]

若满足式\(\eqref{Conservation}\)，则：

\[\tilde{\mathbf{A}} = \tilde{\mathbf{C}}\tilde{\mathbf{B}}^{-1} \]

通过式\(\eqref{jump_q}\)可得：

\[\tilde{\mathbf{B}} = \begin{bmatrix} 2\tilde q_1 & 0 \\ \tilde q_2 & \tilde q_1 \end{bmatrix} ; \quad \tilde{\mathbf{C}} = \begin{bmatrix} \tilde q_2 & \tilde q_1 \\ 2a^2\tilde q_1 & 2\tilde q_2^2 \end{bmatrix} \]

由此可得Roe平均矩阵：

\[\tilde{\mathbf{A}} = \begin{bmatrix} 0 & 1 \\ a^2 - \tilde u^2 & 2\tilde u \end{bmatrix} \]

其中\(\tilde u\)为Roe平均速度：

\[\tilde u = \frac{\sqrt{\rho_L}u_L + \sqrt{\rho_R}u_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \]

得到\(\tilde{\mathbf{A}}\)以后可得其特征值：

\[\tilde \lambda_1 = \tilde u - a, \quad \tilde \lambda_2 = \tilde u + a \]

右特征向量：

\[\tilde{\mathbf{K}}^{(1)} = \begin{bmatrix} 1 \\ \tilde u-a \end{bmatrix}, \quad \tilde{\mathbf{K}}^{(2)} = \begin{bmatrix} 1 \\ \tilde u+a \end{bmatrix} \]

以上两个向量线性无关，满足条件1。求解波强度\(\tilde{\alpha}_{i}\)：

\[\Delta{\mathbf{U}} = \begin{bmatrix} \Delta u_1 \\ \Delta u_2 \end{bmatrix} = \sum_{i=1}^{2} \tilde{\alpha}_{i} \tilde{\mathbf{K}}^{(i)} \]

解为：

\[\alpha_{1} = \frac{\Delta u_1(\tilde u+a) - \Delta u_2 }{2a} \\ \alpha_{2} = \frac{-\Delta u_1(\tilde u-a) + \Delta u_2 }{2a} \]

由此可得通量\(\mathbf{F}_{i+\frac{1}{2}}\)

2.2 The Euler Equations

理想气体条件下的三维非稳态在x方向分解的欧拉方程。

\(x\)方向的Exact Jacobian matrix\(\mathbf{A(\mathbf{U})}\)：

\[\mathbf{A} = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ \hat{\gamma}H-u^2-a^2 & (3-\gamma)u & -\hat{\gamma}v & -\hat{\gamma} w & \hat{\gamma} \\ -uv & v & u & 0 & 0 \\ -uw & w & 0 & u & 0 \\ \frac{1}{2}u[(\gamma -3)H -a^2] & H - \hat{\gamma}U^2 & -\hat{\gamma}uv & \hat{\gamma}uw & \gamma u \end{bmatrix} \]

其中\(\hat{\gamma} = \gamma - 1\)。特征值为：

\[\lambda_1 = u - a \qquad \lambda_2 =\lambda_3 =\lambda_4 = u \qquad \lambda_5 = u + a \]

其中\(a = \sqrt{\gamma p / \rho}\)为音速，相应的右特征向量：

\[\mathbf{K}^{(1)} = \begin{bmatrix} 1 \\ u-a \\v \\ w \\ H-ua \end{bmatrix} ;\quad \mathbf{K}^{(2)} = \begin{bmatrix} 1 \\ u \\v \\ w \\ \frac{1}{2}V^2 \end{bmatrix} ;\quad \mathbf{K}^{(3)} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ v \end{bmatrix} ; \\ \mathbf{K}^{(4)} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ w \end{bmatrix} ; \qquad \mathbf{K}^{(5)} = \begin{bmatrix} 1 \\ u+a \\v \\ w \\ H+ua \end{bmatrix} \]

其中\(H\)为总焓：

\[H = \frac{E + p}{\rho} \]

\(E\)为总能per unit volume：

\[E = \frac{1}{2} \rho \mathbf{V}^2 + \rho e \]

\(e\)：specific internal energy

\[e = \frac{p}{(\gamma -1)\rho} \]

选择参数向量：

\[\mathbf{Q} = \begin{bmatrix} q_1 \\ q_2 \\ q_3 \\ q_4 \\ q_5 \end{bmatrix} = \sqrt{\rho} \begin{bmatrix} 1 \\ u \\ v \\ w \\ H \end{bmatrix} \]

这样子通量中的每个部分对参数均为二次函数。比如：\(u_1 = q_1^2, \quad f_1 = q_1q_2\)。这个性质对于\(\mathbf{G}, \mathbf{H}\)也成立。

与isothermal equations相同，把\(\Delta \mathbf{U}\)和\(\Delta \mathbf{F}\)通过矩阵\(\tilde{\mathbf{B}}\)和 \(\tilde{\mathbf{C}}\)写成$$\Delta \mathbf{Q}$$的函数。Roe给出以下形式：

\[\tilde{\mathbf{B}} =\begin{bmatrix} 2\tilde q_1 & 0 & 0 & 0 & 0 \\ \tilde q_2 & \tilde q_1 & 0 & 0 & 0 \\ \tilde q_3 & 0 & \tilde q_1 & 0 & 0 \\ \tilde q_4 & 0 & 0 & \tilde q_1 & 0\\ \frac{\tilde q_5}{\gamma} & \frac{\gamma-1}{\gamma}\tilde q_2 & \frac{\gamma-1}{\gamma}\tilde q_3 & \frac{\gamma-1}{\gamma}\tilde q_4 & \frac{\tilde q_1}{\gamma} \end{bmatrix} \]

和

\[\tilde{\mathbf{C}} = \begin{bmatrix} \tilde q_2 & \tilde q_1 & 0 & 0 & 0 \\ \frac{\gamma-1}{\gamma}\tilde q_5 & \frac{\gamma+1}{\gamma}\tilde q_2 & -\frac{\gamma-1}{\gamma}\tilde q_3 & -\frac{\gamma-1}{\gamma}\tilde q_4 & \frac{\gamma-1}{\gamma}\tilde q_1 \\ 0 & \tilde q_3 & \tilde q_2 & 0 & 0 \\ 0 & \tilde q_4 & 0 & \tilde q_2 & 0 \\ 0 & \tilde q_5 & 0 & 0 & \tilde q_2 \end{bmatrix} \]

可得Roe近似矩阵：

\[\tilde{\mathbf{A}} = \tilde{\mathbf{C}}\tilde{\mathbf{B}}^{-1} \]

矩阵\(\tilde{\mathbf{A}} = \tilde{\mathbf{C}}\tilde{\mathbf{B}}^{-1}\)的特征值：

\[\tilde \lambda_1 = \tilde u - \tilde a, \quad \tilde \lambda_2 = \tilde \lambda_3 = \tilde \lambda_4 = \tilde u , \quad \tilde \lambda_5 = \tilde u + \tilde a \label{averaged eigenvalues} \]

\[\tilde{\mathbf{K}}^{(1)} = \begin{bmatrix} 1 \\ \tilde u - \tilde a \\ \tilde v \\ \tilde w \\ \tilde H-\tilde u \tilde a \end{bmatrix} ;\quad \tilde{\mathbf{K}}^{(2)} = \begin{bmatrix} 1 \\ \tilde u \\ \tilde v \\ \tilde w \\ \frac{1}{2}\tilde V^2 \end{bmatrix} ;\quad \tilde{\mathbf{K}}^{(3)} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ \tilde v \end{bmatrix} ; \\ \tilde{\mathbf{K}}^{(4)} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ \tilde w \end{bmatrix} ; \qquad \tilde{\mathbf{K}}^{(5)} = \begin{bmatrix} 1 \\ \tilde u+ \tilde a \\ \tilde v \\ \tilde w \\ \tilde H+\tilde u \tilde a \end{bmatrix} \label{averaged right eigenvectors} \]

相应的均值：

\[\tilde u = \frac{\sqrt{\rho_L}u_L + \sqrt{\rho_R}u_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde v = \frac{\sqrt{\rho_L}v_L + \sqrt{\rho_R}v_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde w = \frac{\sqrt{\rho_L}w_L + \sqrt{\rho_R}w_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde H = \frac{\sqrt{\rho_L}H_L + \sqrt{\rho_R}H_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde a = \left( (\gamma - 1)(\tilde H - \frac{1}{2} \tilde V^2) \right)^{\frac{1}{2}} \label{Roe average values} \]

为了得到Roe通量\(\mathbf{F}_{\frac{1}{2}}\)，需要得到波强度，通过求解以下公式。

\[\Delta \mathbf{U} = \sum_{1}^{5} \tilde{\alpha}_i \hat{\mathbf{K}}^{(i)} \]

展开：

\[\tilde{\alpha}_1 + \tilde{\alpha}_2 + \tilde{\alpha}_5 = \Delta u_1 \\ \tilde{\alpha}_1 (\tilde{u} - \tilde{a}) + \tilde{\alpha}_2 \tilde{u} + \tilde{\alpha}_5 (\tilde{u} + \tilde{a}) = \Delta u_2 \\ \tilde{\alpha}_1 \tilde{v} + \tilde{\alpha}_2 \tilde{v} + \tilde{\alpha}_3 + \tilde{\alpha}_5 \tilde{v} = \Delta u_3 \\ \tilde{\alpha}_1 \tilde{w} + \tilde{\alpha}_2 \tilde{w} + \tilde{\alpha}_4 + \tilde{\alpha}_5 \tilde{w} = \Delta u_4 \\ \tilde{\alpha}_1 (\tilde H-\tilde u \tilde a) + \frac{1}{2}\tilde V^2 \tilde{\alpha}_2 + \tilde{\alpha}_3 \tilde{v} + \tilde{\alpha}_4 \tilde{w} + \tilde{\alpha}_5 (\tilde H+\tilde u \tilde a) = \Delta u_5 \label{wave strengths} \]

在计算以上方程组之前，可以先考虑一维的情况，此时：

\[\tilde{v} + \tilde{w} = 0, \qquad \tilde{\alpha}_3 = \tilde{\alpha}_4 = 0, \qquad \tilde{\mathbf{K}}^{(3)} = \tilde{\mathbf{K}}^{(4)} = 0 \]

对于在x方向分解的三维问题，和一维问题相同。

\[\tilde{\alpha}_3 = \Delta u_3 - \tilde{v} \Delta u_1 \qquad \tilde{\alpha}_4 = \Delta u_4 - \tilde{w} \Delta u_1 \]

然后可求出\(\tilde{\alpha}_1, \tilde{\alpha}_2, \tilde{\alpha}_5\)

算法流程：

通过以下步骤计算Roe通量\(\mathbf{F}_{\frac{1}{2}}\)：

1. 通过\(\eqref{Roe average values}\)计算均值\(\tilde u, \tilde v, \tilde w, \tilde H, \tilde a\)。
2. 通过\(\eqref{averaged eigenvalues}\)计算平均特征值\(\tilde\lambda_i\)。
3. 通过\(\eqref{averaged right eigenvectors}\)计算平均右特征向量\(\tilde{\mathbf{K}}^{(i)}\)。
4. 通过\(\eqref{wave strengths}\)计算波强度\(\tilde\alpha_i\)。
5. 用以上结果计算Roe通量\(\mathbf{F}_{\frac{1}{2}}\)。

3. The Roe–Pike Method

通过Roe格式算通量，需要计算平均特征值\(\tilde\lambda_i\)， 平均右特征向量\(\tilde{\mathbf{K}}^{(i)}\)， 波强度\(\tilde\alpha_i\)。上述为原始的Roe格式，在这个格式中首先考虑平均Jacobian矩阵。Roe and Pike提出的方法则可以绕开构造这一矩阵。在这个方法中，直接得到平均量，然后计算出特征值，右特征向量和波强度。

3.1 The Approach

前提：守恒律方程为双曲方程，能够解析地得到特征值\(\lambda_i\)和一组线性无关的右特征向量\(\mathbf{K}^{(i)}\)。然后选择一组数量组成向量，一般使用原始变量组成的向量\(\mathbf{W}\)，然后得到该向量的平均向量\(\tilde{\mathbf{W}}\)，然后直接在平均值\(\tilde{\mathbf{W}}\)处解析地得到\(\lambda_i, \mathbf{K}^{(i)}, \hat{\alpha}_i\)。在Roe–Pike格式中主要分为两步。

Linearisation about a Reference State（在参考状态下线性化）

为了解析地得到波强度\(\hat{\alpha}_i\)，基于左值\(\mathbf{U}_L\)和右值\(\mathbf{U}_R\)二阶\(O(\Delta^2)\)接近参考状态\(\hat{\mathbf{U}}\)，Roe and Pike假设一个线性形式的控制方程：

\[\mathbf{U}_{t} + \mathbf{F}(\mathbf{U})_{x} = \mathbf{U}_{t} + \frac{\partial \mathbf{F}}{\partial \mathbf{F}}\mathbf{U}_{x} \approx \mathbf{U}_{t} + \hat{\mathbf{A}}\mathbf{U}_x = 0 \]

其中\(\hat{\mathbf{A}}\) 是Jacobian矩阵，假设已知，使用参考状态\(\hat{\mathbf{U}}\) 计算。特征值和右特征向量也一样。线性黎曼问题：

\[\mathbf{U}_{t} + \hat{\mathbf{A}}\mathbf{U}_x = 0 \\ \mathbf{U}(x, 0) = \left\{\begin{matrix} \mathbf{U}_L & \text{if} \quad x < 0\\ \mathbf{U}_R & \text{if} \quad x > 0 \end{matrix}\right. \]

的 波强度\(\tilde\alpha_i\)通过分解\(\Delta \mathbf{U}\)至右特征向量求解。即求解：

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L = \sum_{k=1}^{m} \hat{\alpha}_k \hat{\mathbf{K}}^{(k)} \]

注意：这个线性化不是从Roe Matrix \(\tilde{\mathbf{A}}\)中得到的Roe线性化。这仅仅是为了寻找波强度的解析解，可以通过未知的Roe–Pike average state \(\tilde{\mathbf{W}}\)计算。

The Algebraic Problem for the Average State

为了求解Roe–Pike average vector \(\tilde{\mathbf{W}}\) ，首先：

\[\tilde{\alpha}_i = \hat{\alpha}_i(\tilde{\mathbf{W}}), \qquad \tilde{\lambda}_i = \lambda_i(\tilde{\mathbf{W}}), \qquad \tilde{\mathbf{K}}^{(i)} = \mathbf{K}^{(i)}(\tilde{\mathbf{W}}) \]

\(\hat{\alpha}_i, \lambda_i, \mathbf{K}^{(i)}\)的解析解在未知状态\(\tilde{\mathbf{W}}\)处计算。\(\tilde{\mathbf{W}}\)通过求解以下代数方程求解：

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L = \sum_{k=1}^{m}\tilde{\alpha}_k \tilde{\mathbf{K}}^{(k)} \]

和：

\[\Delta \mathbf{F} = \mathbf{F}_R - \mathbf{F}_L = \sum_{k=1}^{m}\tilde{\alpha}_k \tilde{\lambda}_k \tilde{\mathbf{K}}^{(k)} \]

3.2 The Isothermal Equations

通过Roe–Pike approach求解isothermal equations方程的黎曼问题：

\[\mathbf{U}_{t} + \mathbf{F}(\mathbf{U})_{x} = 0 \\ \mathbf{U}(x,0) = \left\{\begin{matrix} \mathbf{U}_{L} & \text{if } x < 0 \\ \mathbf{U}_{R} & \text{if } x > 0 \end{matrix}\right. \]

真正的Jacobian 矩阵，特征值和右特征向量为：

\[\mathbf{A(\mathbf{U})} = \begin{bmatrix} 0 & 1 \\ a^2-u^2 & 2u \end{bmatrix} \\ \lambda_1 = u - a, \quad \lambda_2 = u + a \\ \mathbf{K}^{(1)} = \begin{bmatrix} 1 \\ u-a \end{bmatrix}, \quad \mathbf{K}^{(2)} = \begin{bmatrix} 1 \\ u+a \end{bmatrix} \]

Linearisation about a Reference State

在\(\hat{\mathbf{U}}\)处线性化黎曼问题：

\[\mathbf{U}_{t} + \hat{\mathbf{A}}\mathbf{U}_{x} = 0 \\ \mathbf{U}(x,0) = \left\{\begin{matrix} \mathbf{U}_{L} & \text{if } x < 0 \\ \mathbf{U}_{R} & \text{if } x > 0 \end{matrix}\right. \]

其中\(\hat{\mathbf{A}}\)是在参考状态\(\hat{\mathbf{U}}\)处计算的Jacobian矩阵，原始变量的形式为\(\hat{\mathbf{W}} = \{\hat{\rho}, \hat{u} \}^{T}\)。完整的特征结构为：

\[\mathbf{A(\mathbf{U})} = \begin{bmatrix} 0 & 1 \\ a^2-\hat u^2 & 2\hat u \end{bmatrix} \\ \lambda_1 = \hat u - a, \quad \lambda_2 = \hat u + a \\ \mathbf{K}^{(1)} = \begin{bmatrix} 1 \\ \hat u-a \end{bmatrix}, \quad \mathbf{K}^{(2)} = \begin{bmatrix} 1 \\ \hat u+a \end{bmatrix} \]

分解\(\Delta \mathbf{U}\)

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L = \sum_{k=1}^{m}\hat{\alpha}_k \hat{\mathbf{K}}^{(k)} \]

展开：

\[\Delta{\rho} = \rho_R - \rho_L = \hat{\alpha}_1 + \hat{\alpha}_2 \\ \Delta{(\rho u)} = (\rho u)_R - (\rho u)_L = \hat{\alpha}_1 (\hat{u} - a) + \hat{\alpha}_2(\hat{u} + a) \]

其中：

\[\Delta{(\rho u)} = \hat{\rho}\Delta u + \hat{u}\Delta \rho + O(\Delta^2) \]

其中the leading term in\(O(\Delta^2)\)为：

\[(\rho_R - \hat{\rho})(u_R - \hat{u}) - (\rho_L - \hat{\rho})(u_L - \hat{u}) \]

忽略\(O(\Delta^2)\)：

\[\hat{\rho}\Delta u + \hat{u}\Delta \rho = \hat{\alpha}_1 (\hat{u} - a) + \hat{\alpha}_2(\hat{u} + a) \]

求解后可得：

\[\hat{\alpha}_1 = \frac{1}{2} \left[ \Delta \rho - \hat{\rho}\frac{\Delta u}{a} \right] \\ \hat{\alpha}_1 = \frac{1}{2} \left[ \Delta \rho + \hat{\rho}\frac{\Delta u}{a} \right] \]

与原始的Roe格式得到的波强度相比，在二阶精度\(O(\Delta^2)\)的范围内，一致，故以下两组方程满足：

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L = \sum_{k=1}^{2}\hat{\alpha}_k \hat{\mathbf{K}}^{(k)} \\ \Delta \mathbf{F} = \mathbf{F}_R - \mathbf{F}_L = \sum_{k=1}^{2}\hat{\alpha}_k \hat{\lambda}_k \hat{\mathbf{K}}^{(k)} \]

对于第二组方程，展开后可得：

\[\Delta (\rho u) = \hat{\alpha}_1 \hat{\lambda}_1 + \hat{\alpha}_2 \hat{\lambda}_2 \\ \Delta(\rho u^2 + \rho a^2) = \hat{\alpha}_1 \hat{\lambda}_1 (\hat{u} - a) + \hat{\alpha}_2 \hat{\lambda}_2 (\hat{u} + a) \]

上式的第一个方程展开：

\[\hat{\rho}\Delta u + \hat{u}\Delta \rho = \hat{u}(\hat \alpha_1 + \hat \alpha_2) + a(\hat \alpha_1 - \hat \alpha_2) \]

第二个方程右侧展开：

\[\Delta(\rho u^2 + \rho a^a) = 2 \hat \rho\hat u \Delta u + \hat{u}^2 \Delta \rho + a^2 \Delta \rho \]

右侧可以表述为：

\[(\hat{\alpha}_1 + \hat{\alpha}_2)(\hat{u}^2 + a^2) + 2\hat u a (\hat{\alpha}_2 - \hat{\alpha}_1) \]

The Algebraic Problem for the Average State

Roe–Pike 方法通过代数问题寻找满足以下条件的均值：

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L = \sum_{k=1}^{2}\tilde{\alpha}_k \tilde{\mathbf{K}}^{(k)} \\ \Delta \mathbf{F} = \mathbf{F}_R - \mathbf{F}_L = \sum_{k=1}^{2}\tilde{\alpha}_k \tilde{\lambda}_k \hat{\mathbf{K}}^{(k)} \label{condition} \]

特征结构可写为：

\[\tilde{\alpha}_1 = \frac{1}{2} \left[ \Delta \rho - \tilde{\rho}\frac{\Delta u}{a} \right], \qquad \tilde{\alpha}_1 = \frac{1}{2} \left[ \Delta \rho + \tilde{\rho}\frac{\Delta u}{a} \right] \\ \tilde{\lambda}_1 = \tilde{u} - a, \qquad \tilde{\lambda}_2 = \tilde{u} + a \\ \tilde{\mathbf{K}}^{(1)} = \begin{bmatrix} 1 \\ \tilde{u} - a \end{bmatrix}, \qquad \tilde{\mathbf{K}}^{(2)} = \begin{bmatrix} 1 \\ \tilde{u} + a \end{bmatrix} \]

展开\(\eqref{condition}\)可得：

\[\Delta \rho = \tilde{\alpha}_1 + \tilde{\alpha}_2 \qquad \text{(a)} \\ \Delta{(\rho u)} = \tilde{\alpha}_1 (\tilde{u} - a) + \tilde{\alpha}_2(\tilde{u} + a) \qquad \text{(b)} \\ \Delta{(\rho u)} = \tilde{\lambda}_1 \tilde{\alpha}_1 + \tilde{\lambda}_2 \tilde{\alpha}_2 \qquad \text{(c)} \\ \Delta(\rho u^2 + \rho a^2) = \tilde{\alpha}_1 \tilde{\lambda}_1 (\tilde{u} - a) + \tilde{\alpha}_2 \tilde{\lambda}_2 (\tilde{u} + a) \qquad \text{(d)} \]

四个方程，求解两个未知数\(\tilde{\rho}, \tilde{u}\)。但是公式（a）无条件满足，公式（b）和公式（c）一致，所以最后只需要联立（c）和（d）即可求解。

从（c）中可得

\[\Delta(\rho u) = \tilde{u}(\tilde \alpha_1 + \tilde \alpha_2) + a(\tilde \alpha_1 - \tilde \alpha_2) \]

带入波强度公式：

\[\Delta(\rho u) = \tilde{\rho}\Delta u + \tilde{u} \Delta \rho \]

公式（d）可以写为：

\[\Delta(\rho u^2 + \rho a^2) = (\tilde{\alpha}_1 + \tilde{\alpha}_2)(\tilde{u}^2 + a^2) + 2\tilde u a (\tilde{\alpha}_2 - \tilde{\alpha}_1) \]

带入波强度：

\[\Delta(\rho u^2 + \rho a^2) = \Delta(\rho u^2) + a^2 \Delta \rho \]

此处省略求解过程！

最终结果：

\[\tilde{u} = \frac{\Delta (\rho u \pm \Delta u \sqrt{\rho_L \rho_R})}{\Delta \rho} \]

应该取负号：

\[\tilde{u} = \frac{\sqrt{\rho_L}u_L + \sqrt{\rho_R}u_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \]

密度：

\[\tilde{\rho} = \sqrt{\rho_L \rho_R} \]

取负号的时候，会引起数值波动。

3.3 The Euler Equations

对于欧拉方程的黎曼问题：

\[\mathbf{U}_{t} + \hat{\mathbf{A}}\mathbf{U}_{x} = 0 \\ \mathbf{U}(x,0) = \left\{\begin{matrix} \mathbf{U}_{L} & \text{if } x < 0 \\ \mathbf{U}_{R} & \text{if } x > 0 \end{matrix}\right. \]

特征值：

\[\hat \lambda_1 = \hat u - \hat a, \quad \hat \lambda_2 = \hat \lambda_3 = \hat \lambda_4 = \hat u , \quad \hat \lambda_5 = \hat u + \hat a \]

特征向量：

\[\hat{\mathbf{K}}^{(1)} = \begin{bmatrix} 1 \\ \hat u - \hat a \\ \hat v \\ \hat w \\ \hat H-\hat u \hat a \end{bmatrix} ;\quad \hat{\mathbf{K}}^{(2)} = \begin{bmatrix} 1 \\ \hat u \\ \hat v \\ \hat w \\ \frac{1}{2}\hat V^2 \end{bmatrix} ;\quad \hat{\mathbf{K}}^{(3)} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ \hat v \end{bmatrix} ; \\ \hat{\mathbf{K}}^{(4)} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ \hat w \end{bmatrix} ; \qquad \hat{\mathbf{K}}^{(5)} = \begin{bmatrix} 1 \\ \hat u+ \hat a \\ \hat v \\ \hat w \\ \hat H+\hat u \hat a \end{bmatrix} \]

展开\(\Delta \mathbf{U}\) ：

\[\Delta \mathbf{U} = \sum_{1}^{5} \hat{\alpha}_i \hat{\mathbf{K}}^{(i)} \]

求解上述方程，可得波强系数\(\hat{\alpha}_i\) ：

\[\hat{\alpha}_3 = \Delta u_3 - \hat{v}\Delta u_1 \\ \hat{\alpha}_4 = \Delta u_4 - \hat{w}\Delta u_1 \\ \hat{\alpha}_2 = \frac{\gamma - 1}{\hat{a}^2}[\Delta u_1 (\hat{H} - \hat{u}^2) + \hat{u}\Delta u_2 - \overline{\Delta u_5}] \\ \hat{\alpha}_1 = \frac{1}{2\hat{a}}[\Delta u_1(\hat{u} + \hat{a}) - \Delta u_2 - \hat{a}\hat{\alpha}_2] \\ \hat{\alpha}_5 = \Delta u_1 - (\hat{\alpha}_1 + \hat{\alpha}_2) \]

二阶近似后可得：

\[\hat{\alpha}_1 = \frac{1}{2\hat{a}^2}[\Delta p - \hat{\rho}\hat{a}\Delta u] \\ \hat{\alpha}_2 = \Delta \rho - \Delta p / \hat{a}^2 \\ \hat{\alpha}_3 = \hat{\rho}\Delta v \\ \hat{\alpha}_4 = \hat{\rho}\Delta w \\ \hat{\alpha}_3 = \frac{1}{2\hat{a}^2}[\Delta p + \hat{\rho}\hat{a}\Delta u] \]

第二步：寻找均值状态

\[\tilde{\mathbf{W}} = (\tilde{\rho}, \tilde{u}, \tilde{v}, \tilde{w}, \tilde{a})^T \]

求解：

\[\Delta \mathbf{U} = \mathbf{U}_R - \mathbf{U}_L = \sum_{k=1}^{2}\tilde{\alpha}_k \tilde{\mathbf{K}}^{(k)} \\ \Delta \mathbf{F} = \mathbf{F}_R - \mathbf{F}_L = \sum_{k=1}^{2}\tilde{\alpha}_k \tilde{\lambda}_k \hat{\mathbf{K}}^{(k)} \]

其中：

\[\tilde{\alpha}_i = \hat{\alpha}_i(\tilde{\mathbf{W}}), \qquad \tilde{\lambda}_i = \lambda_i(\tilde{\mathbf{W}}), \qquad \tilde{\mathbf{K}}^{(i)} = \mathbf{K}^{(i)}(\tilde{\mathbf{W}}) \]

得到解为：

\[\tilde{\rho} = \sqrt{\rho_L \rho_R} \\ \tilde{u} = \frac{\sqrt{\rho_L}u_L + \sqrt{\rho_R}u_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde{v} = \frac{\sqrt{\rho_L}v_L + \sqrt{\rho_R}v_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde{w} = \frac{\sqrt{\rho_L}w_L + \sqrt{\rho_R}w_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde{H} = \frac{\sqrt{\rho_L}H_L + \sqrt{\rho_R}H_R}{\sqrt{\rho_L} + \sqrt{\rho_R}} \\ \tilde{a} = \left( (\gamma - 1)(\tilde{H} - \frac{1}{2}\tilde{\mathbf{V}}^2) \right)^{\frac{1}{2}} \label{average} \]

算法

1. 根据\(\eqref{average}\)计算均值。
2. 通过均值计算特征值
3. 通过均值计算特征向量
4. 通过均值计算波强
5. 用以上结果求解Roe通量

4. An Entropy Fix

线性化的黎曼问题只包含了间断跳跃，对于激波和接触间断是一个很好的近似，但是对于接触间断则会有一些错误。但是在实际使用中，只有跨音速的接触间断会影响面通量。此时会引起entropy violating discontinuous waves，这种现象也被叫为rarefaction shocks。

4.1 The Entropy Problem

对于作稀疏波，满足以下条件的时候是跨音速稀疏波：

波头速度：

\[\lambda_1(\mathbf{U}_L) = S_{HL} = u_L - a_L < 0 \]

波尾速度：

\[\lambda_1(\mathbf{U}_{*L}) = S_{HL} = u_* - a_{*L} > 0 \]

可以修正Roe 求解器以避免这一问题。

4.2 The Harten–Hyman Entropy Fix

主要说明非稳态欧拉方程的熵修正问题，此时只需要考虑左右两侧的非线性波，其特征值为\(\lambda_1 = u - a\)和\(\lambda_5 = u +a\)。熵修正依赖对速度\(u_*\)以及星号区域内左右音速\(a_{*L}, a_{*R}\)。

Left Transonic Rarefaction

假设速度\(u_*\)以及星号区域内左右音速\(a_{*L}, a_{*R}\) 已知， 波速：

\[\lambda_1^L = u_L - a_L ,\qquad \lambda_1^R = u_* - a_{*L} \]

如果

\[\lambda_1^L < 0 <\lambda_1^R \]

则左侧的波为跨音速稀疏波。这种情况下，熵修正按照以下形式。单个间断：

\[\mathbf{U}_{*L} - \mathbf{U}_{L} = \tilde{\alpha}_1 \tilde{\mathbf{K}}^{(1)} \]

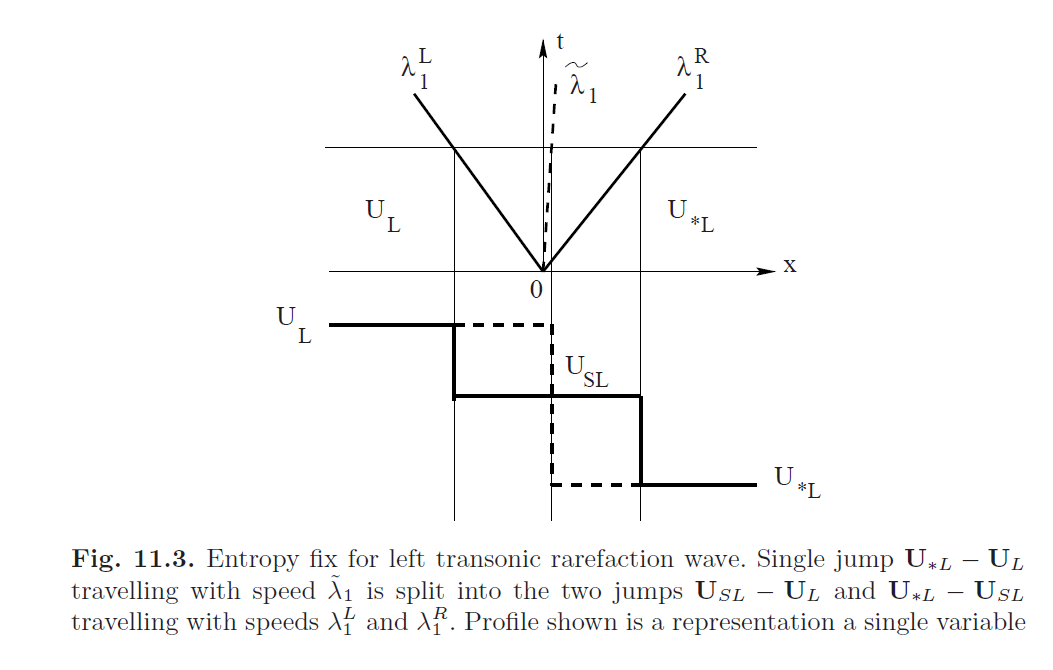
以\(\tilde{\lambda}_1\)的速度传播。此间断分解成两个间断\(\mathbf{U}_{SL} - \mathbf{U}_{L}\)和\(\mathbf{U}_{*L} - \mathbf{U}_{SL}\) ，其传播速度分别为\(\lambda_1^L\)和\(\lambda_1^R\)，此时需要找到\(\mathbf{U}_{SL}\)这一中间态。结构如图11.3所示。

使用积分形式的守恒率得：

\[\lambda_1^R (\mathbf{U}_{SL} - \mathbf{U}_{*L}) + \lambda_1^L(\mathbf{U}_{L} - \mathbf{U}_{SL}) = \tilde{\lambda}_1 (\mathbf{U}_{L} - \mathbf{U}_{*L}) \label{int con} \]

由此可得：

\[\mathbf{U}_{SL} = \frac{(\tilde{\lambda}_1 - \lambda_1^L)\mathbf{U}_{L} + (\lambda_1^R - \tilde{\lambda}_1) \mathbf{U}_{*L}}{\lambda_1^R - \lambda_1^L} \]

计算Roe通量时，则采用单边：

\[\mathbf{F}_{i+\frac{1}{2}} = \mathbf{F}_L + \sum_{\tilde{\lambda}_k \le 0} \tilde{\lambda}_k \tilde{\alpha}_k \tilde{\mathbf{K}}^{(k)} \]

对于本例，只有间断\(\mathbf{U}_{SL} - \mathbf{U}_{L}\)的传播速度\(\lambda_1^L < 0\)。化简\(\eqref{int con}\)得：

\[\mathbf{U}_{SL} - \mathbf{U}_{L}= \frac{\lambda_1^R - \tilde{\lambda}_1}{\lambda_1^R - \lambda_1^L}(\mathbf{U}_{*L} - \mathbf{U}_{L}) \]

Roe近似：

\[\lambda_1^R - \lambda_1^L = \tilde{\alpha}_1 \tilde{\mathbf{K}}^{(1)} \]

通量跳跃可写为：

\[(\Delta F)_1^L = \lambda_1^L \left(\frac{\lambda_1^R - \tilde{\lambda}_1}{\lambda_1^R - \lambda_1^L} \right) \tilde{\alpha}_1 \tilde{\mathbf{K}}^{(1)} \]

则波速可写为：

\[\overline{\lambda}_1 = \lambda_1^L \left(\frac{\lambda_1^R - \tilde{\lambda}_1}{\lambda_1^R - \lambda_1^L} \right) \]

通量可写为：

\[\mathbf{F}_{i+\frac{1}{2}} = \mathbf{F}_L + \overline{\lambda}_1 \tilde{\alpha}_1 \tilde{\mathbf{K}}^{(1)} \]

Right Transonic Rarefaction

与左侧同理

4.3 The Speeds \(u_*, a_{*L}, a_{*R}\)

此时需要计算星号区域内的参数。有以下几种方法：

1. The Roe–Averaged States
2. The PVRS Approximation
3. TRRS Approximation