AVL树

AVL树：强平衡二叉搜索树， 约定其 左右子节点高度差  <= 1；

图片、代码参考：Deletion in an AVL Tree - GeeksforGeeks

为保证这种平衡性；每次插入删除操作，都需要维护这条路径上节点的平衡性；因此不适合频繁插入删除，时间复杂度趋近O(log h)；这也是红黑树优势的地方，是弱平衡；

维护节点平衡的四种旋转方式：基本的是前两种，左旋和右旋，后两种是组合旋转；

1、LLrotation：

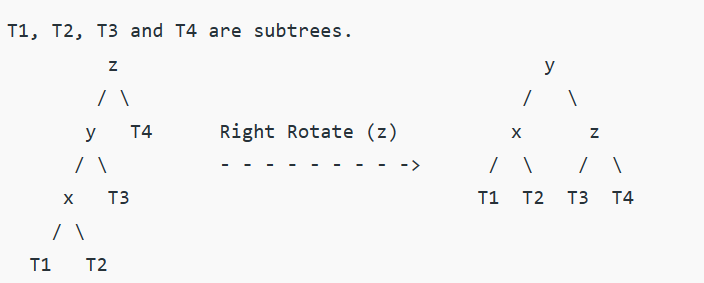
2、RRrotation：

3、LRrotation：先左旋后右旋

 

 4、RLrotation：先右旋后左旋

 

插入操作：

1、递归找到插入位置； 2、维护平衡性；

删除操作：

递归找到要删除的节点；分为三种情况：①、删除叶子节点   ②、删除左右子节点有一个为空的父节点； ③、删除左右子节点都不为空的父节点；

1、叶子节点：直接删除即可；

2、只有一个字节点：用这个子节点覆盖要删除的节点；这儿意味着子节点没有子节点了，不然不满足avl平衡树的性质，所以采用直接 值赋值；

3、左右子节点存在：找到后继节点：右子树中最小的节点，也就是中序遍历中要删除节点的下一个；将值赋值给要删除的节点；之后右子节点继续递归删除，这个后继节点的值；

4、三种情况处理完后，向上维护节点的平衡性；因为存在递归，所以在递归返回时，递归路径中的节点，会从下到上依次检查路径节点平衡性；

 具体实现：

#include <bits/stdc++.h>
using namespace std;

struct Node{
    int data;
    Node* left, *right;
    int height;
};

int height(Node* node){
    if(node == nullptr) return 0;
    return node->height;
}
Node* LLrotation(Node* node){
    Node* tmp = node->left;
    Node* t = tmp->right;
    tmp->right = node;
    node->left = t;
    node->height = max(height(node->left), height(node->right)) + 1;
    tmp->height = max(height(tmp->right), height(tmp->left)) + 1;
    return tmp;
}
Node* RRrotation(Node* node){
    Node* tmp = node->right;
    Node* t = tmp->left;
    tmp->left = node;
    node->right = t;
    node->height = max(height(node->left), height(node->right)) + 1;
    tmp->height = max(height(tmp->left), height(tmp->right)) + 1;
    return tmp;
}
int balance_factor(Node* t){
    if(t == nullptr) return 0;
    return height(t->left) - height(t->right);
}
Node* successor(Node* t){
    Node* cur = t;
    while(cur->left != nullptr){
        cur = cur->left;
    }
    return cur;
}
Node* newNode(int num){
    Node* root = new Node();
    root->data = num;
    root->left = nullptr;
    root->right = nullptr;
    root->height = 1;
    return root;
}
Node* insert(Node* root, int num){
    if(root == nullptr){
        return newNode(num);
    }
    /*recursion: find the insert position*/
    if(num < root->data){
        root->left = insert(root->left, num);
    }else if(num > root->data){
        root->right = insert(root->right, num);
    }else{
        return root;
    }
    
    /*balance <= 1*/
    root->height = 1 + max(height(root->left), height(root->right));
    int bal = balance_factor(root);
    if(bal > 1 && num < root->left->data){
        return LLrotation(root);
    }
    if(bal > 1 && num > root->left->data){
        root->left = RRrotation(root->left);
        return LLrotation(root);
    }
    if(bal < -1 && num > root->right->data){
        return RRrotation(root);
    }
    if(bal < -1 && num < root->right->data){
        root->right = LLrotation(root->right);
        return RRrotation(root);
    }
    return root;
}

Node* deletenode(Node* root, int num){
    if(root == nullptr) return root;
    if(num > root->data){
        root->right = deletenode(root->right, num);
    }else if(num < root->data){
        root->left = deletenode(root->left, num);
    }else{
        if(root->right == nullptr || root->left == nullptr){
            Node* tmp = root->left ? root->left : root->right;
            if(tmp == nullptr){
                root == nullptr;
            }else{
                *root = *tmp;//override;
            }
            delete(tmp);
        }else{
            Node* tmp = successor(root->right);
            root->data = tmp->data;
            root->right = deletenode(root->right, tmp->data);
        }
    }
    /*check balance?  4 cases*/
    if(root == nullptr) return root;
    root->height = max(height(root->left), height(root->right)) + 1;
    int bal = balance_factor(root);

    if(bal > 1 && balance_factor(root->left) >= 0){
        return LLrotation(root);
    }
    if(bal > 1 && balance_factor(root->left) < 0){
        root->left = RRrotation(root->left);
        return LLrotation(root);
    }
    if(bal < -1 && balance_factor(root->right) > 0){
        root->right = LLrotation(root->right);
        return RRrotation(root);
    }
    if(bal < -1 && balance_factor(root->right) <= 0){
        return RRrotation(root);
    }
    return root;
}

int main(){
    Node* root = nullptr;
    int num;
    cout << "input num : ctrl + z is break" << endl;
    /*CTRL + Z : break;*/
    while(cin >> num){
        root = insert(root, num);
    }
    cout << "preorder : " << endl;
    function<void(Node*)>preorder = [&](Node* root){
        if(root == nullptr) return;
        cout << root->data << "\t";
        preorder(root->left);
        preorder(root->right);
    };
    preorder(root);
    
    cin.clear();
    cin.sync();
    cout << endl << "the num to delete:  ctrl + z is break" << endl;
    int tmp;
    while(cin >> tmp){}
    root = deletenode(root, tmp);
    cout << "the arr of after delete: " << endl;
    preorder(root);

    system("pause");
    return 0;
}
/*
input num : ctrl + z is break
9 5 10 0 6 11 -1 1 2^Z
preorder :
9       1       0       -1      5       2       6       10      11
the num to delete:  ctrl + z is break
10
^Z
the arr of after delete:
1       0       -1      9       5       2       6       11      请按任意键继续. . .
*/