KMP(字符串匹配算法)

主要思想：当出现字符不匹配时，可以利用已经匹配的文本内容，避免从头匹配；

考虑文本串：” aabaabaafa“,模式串 ”aabaaf “， 参考「代码随想录」KMP算法详解 - 找出字符串中第一个匹配项的下标 - 力扣（LeetCode），很详细；

个人理解：1、这个算法是对模式串的要求，模式串有重复的字符，并且前缀和后缀是部分相同的，才能用前缀表记录这个信息；此时这个算法才能做到优化 O(N+M）；若模式串没一个重复的相同的，退化为暴力 O(N*M）；

　　　　　2、前后缀相同理解为：该字符串是否具有  从左端开始的子字符串 与 右端开始的子字符串，是否中心对称，必须是从端开始的；此时将相同部分的长度记录到前缀表；例如，模式串中长度为前5个字符的子串aabaa，最长相同前后缀的长度为2，也就是aa部分；前缀表如下；

 

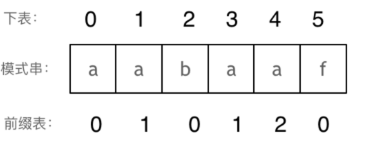
针对前缀表：当遇到不匹配的字符时，看前一个下标，对应的前缀表的数值是多少，就是为了看有没有能重复利用的已经匹配过的字符串；至此就是KMP的原理。

注意：当遇到不匹配的时候，找到前缀表前一个下标的的值，此时模式串跳转到这个下标处，就要开始判断这个下标了，因为前缀表记录的是相等的长度，而下标是从零开始的，所以长度作为下标正好就是下一个要开始判断是否与文本串匹配的字符；

但是具体实现的时候，多数时候是用next数组，就是前缀表的值都减一；这是为了实现方便；

具体实现：

next数组：将next[0 ] = -1; i 代表 前缀终止位置；j 代表后缀终止位置， next[ i] 代表 从零下标当前下标 i 为止 最长相等前后缀长度，就是 j 的值，也就是 对应前缀表的值减一；

void array_Next(int* next, const string& s){
    int j = -1;
    next[0] = -1;
    for(int i = 1; i < s.size();++i){
        while(j >= 0 && s[i] != s[j+1]){
            j = next[j];
        }
        if(s[i] == s[j+1]){
            ++j;
        }
        next[i] = j;
    }
}

字符串匹配：下标j 依然为 -1；与next数组保持一致；

整体实现：

#include <bits/stdc++.h>
using namespace std;

/*KMP(快速模式匹配算法)*/

void array_Next(int* next, const string& s){
    int j = -1;
    next[0] = -1;
    for(int i = 1; i < s.size();++i){
        while(j >= 0 && s[i] != s[j+1]){
            j = next[j];
        }
        if(s[i] == s[j+1]){
            ++j; 
        }
        next[i] = j;
    }
}
int kmp(string& s,string& t){
    int n = s.size();
    int m = t.size();
    int j = -1;
    int next[m];
    array_Next(next, t);
    for(int i = 0;i < n; ++i){
        while(j >= 0 && s[i] != t[j+1]){
            j = next[j];
        }
        if(s[i] == t[j+1]){
            ++j;
        }
        if(j == m - 1){
            return i - m + 1; 
        }
    }
    return -1;
}
int main(){
    string s = "aabaabaafa", t = "aabaaf";

    cout << "index is : " << kmp(s, t) << endl;

    system("pause");
    return 0;
}
/*

index is : 3
请按任意键继续. . .

*/