神经网络与深度学习学习笔记 (二）

神经网络与深度学习学习笔记（二）

性能优化

---

1. 常用技巧

1.1 模型初始化

• 目的
  通过合理的权重初始化避免梯度消失或爆炸，促进网络信息流动。
• 方法
  • 简单初始化：权值在 $$[-1, 1]$$ 区间内按均值或高斯分布初始化。
  • Xavier初始化（适用于激活函数为线性或类线性的场景）：
    \[W \sim U \left[ -\frac{\sqrt{6}}{\sqrt{n_j + n_{j+1}}}, \frac{\sqrt{6}}{\sqrt{n_j + n_{j+1}}} \right] \]
    其中 \(n_j\) 和 \(n_{j+1}\) 分别为当前层和下一层的神经元数量。

---

1.2 数据划分与交叉验证

• 数据划分
  • 训练数据、验证数据、测试数据的典型比例为 70%:15%:15% 或 60%:20%:20%。
  • 数据量较大时，可适当减少训练和验证数据比例。
• K折交叉验证
  • 将原始训练数据分为 \(K\) 个子集，轮流用 \(K-1\) 个子集训练，剩余1个子集验证，重复 \(K\) 次后取平均误差。

---

1.3 欠拟合与过拟合

• 定义
  • 欠拟合：模型在训练集和测试集上误差均较大（模型能力不足）。
  • 过拟合：模型在训练集上误差小，但测试集上误差大（模型过度适应训练数据）。
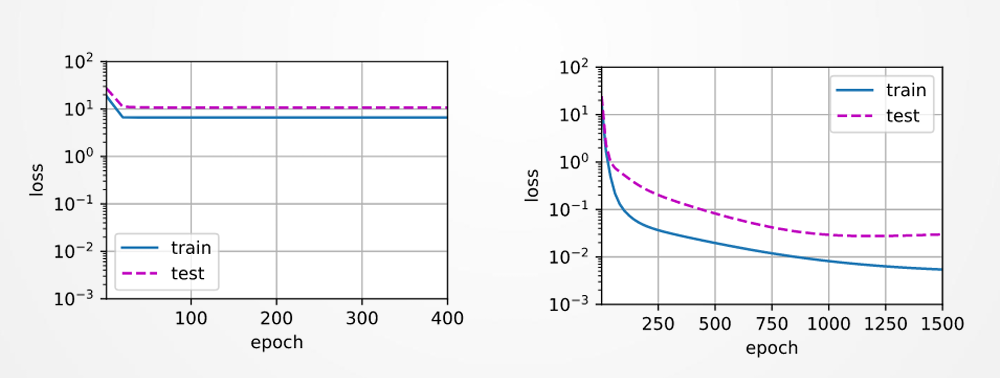
• 图示
  • 过拟合曲线：训练损失持续下降，测试损失先降后升。
    

---

1.4 正则化与Dropout

• 权重衰减（L2正则化）

  • 目标函数加入权值的L2范数惩罚项：
    \[J(w) + \frac{\lambda}{2} \|w\|^2 \]

  • 梯度更新公式：
    \[\frac{\partial J(w)}{\partial w} + \lambda w \]

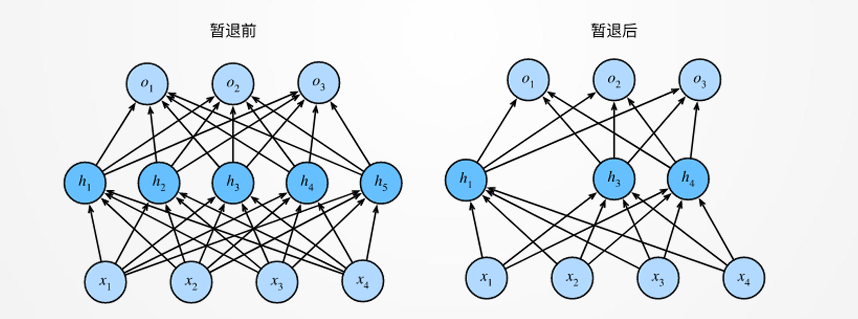
• Dropout

  • 训练时随机将部分神经元输出置零，减少神经元间的共适应性。
  • 测试时保留所有神经元，并对输出按保留概率缩放。
    

---

2. 动量法

2.1 病态曲率问题

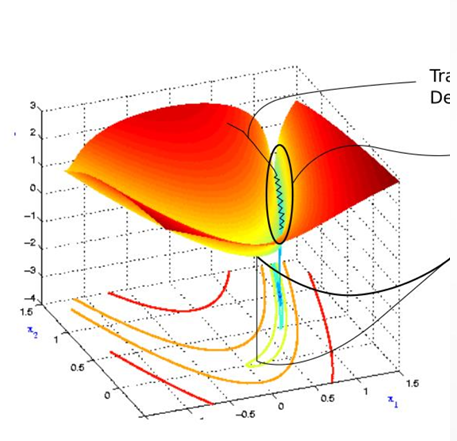
• 现象
  损失函数在局部区域呈现“山沟”状，梯度下降沿山脊震荡，收敛缓慢。
  

• 原因
  参数更新方向在高曲率区域频繁变化，导致优化路径迂回。

2.2 动量法原理

• 类比
  将梯度下降的“纸团”换成“铁球”，利用惯性减少震荡。
• 更新公式
  \[v_t = \alpha v_{t-1} - \epsilon g_t \quad \text{（动量项累加）} \]
  \[\theta_{t+1} = \theta_t + v_t \quad \text{（参数更新）} \]

• 算法步骤
  1. 计算当前梯度 \(g_t\)；
  2. 更新速度 \(v_t\)；
  3. 更新参数 \(\theta\)。

---

3. 自适应梯度算法

3.1 AdaGrad

• 核心思想
  参数学习率自适应调整：历史梯度平方和大的参数学习率小，反之学习率大。
• 更新公式
  \[\Delta \theta = -\frac{\epsilon}{\sqrt{r + \delta}} \odot g \quad \text{（逐元素操作）} \]
  • \(r\) 为梯度平方累积量：\(r \leftarrow r + g \odot g\)。
• 缺点
  学习率单调递减，后期训练可能停滞。

---

3.2 RMSProp

• 改进点
  引入指数衰减平均，减少遥远历史梯度的影响，解决AdaGrad学习率衰减问题。
• 更新公式
  \[r \leftarrow \rho r + (1 - \rho) g \odot g \]
  \[\Delta \theta = -\frac{\epsilon}{\sqrt{r + \delta}} \odot g \]
  • \(\rho\) 控制历史梯度衰减速率（默认0.9）。

---

3.3 Adam

• 核心思想
  结合动量法和RMSProp，同时考虑梯度一阶矩（均值）和二阶矩（方差）。
• 算法步骤
  1. 计算梯度 \(g_t\)；
  2. 更新一阶矩 \(s\) 和二阶矩 \(r\)：
     \(s \leftarrow \rho_1 s + (1 - \rho_1)g_t, \quad r \leftarrow \rho_2 r + (1 - \rho_2)g_t \odot g_t\)
  3. 修正偏差（因初始时刻矩估计偏向0）：
     \(\hat{s} = \frac{s}{1 - \rho_1^t}, \quad \hat{r} = \frac{r}{1 - \rho_2^t}\)
  4. 参数更新：
     \(\Delta \theta = -\epsilon \frac{\hat{s}}{\sqrt{\hat{r} + \delta}}\)
• 优点
  自适应学习率、抗噪声能力强，适合非平稳目标函数。

---

4. 总结

• 常用技巧
  • 合理初始化、数据划分、正则化、Dropout可提升模型泛化能力。
• 动量法
  • 加速收敛，减少病态曲率震荡，但需调整动量因子 \(\alpha\)。
• 自适应算法
  • AdaGrad：简单自适应，但学习率衰减过快；
  • RMSProp：改进衰减问题，适合非凸优化；
  • Adam：综合性能优，广泛用于深度学习任务。

---

实践建议：

• 优先尝试Adam优化器（默认参数 \(\epsilon=0.001, \rho_1=0.9, \rho_2=0.999\)）；
• 结合学习率调度（如预热、衰减）进一步提升效果。

---