神经网络与深度学习学习笔记(一）

神经网络与深度学习学习笔记(一）

---

第一部分：线性回归与分类

1. 线性回归

• 定义
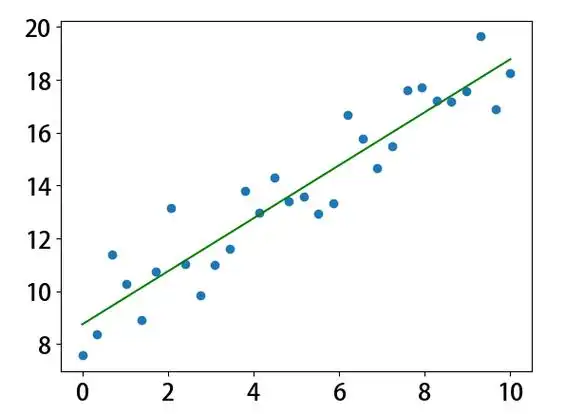
  通过回归分析确定变量间定量关系的统计方法。
  

• 学习过程
  

• 模型
  假设函数：

  • 线性模型：$$y = h_\theta(x) = \theta^T x$$
  • 一维特例：$$y = kx + b$$

• 损失函数（均方误差，MSE）

  \[J(\theta) = \frac{1}{2} \sum_{i=1}^N \left( y^{(i)} - h_\theta(x^{(i)}) \right)^2 \]

• 求解方法
  解析解：$$\theta = (X^T X)^{-1} X^T y$$

---

2. 线性分类

• 与回归的区别

  • 输出为类别概率（0-1），而非连续值。
  • 使用 Sigmoid 函数将线性组合映射到概率：
    \[h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}} \]

• 损失函数（交叉熵损失）

  \[J(\theta) = -\sum_{i=1}^N \left[ y^{(i)} \log h_\theta(x^{(i)}) + (1 - y^{(i)}) \log (1 - h_\theta(x^{(i)})) \right] \]

• 求解方法
  梯度下降法（因损失函数非线性，无法直接求解析解）。

---

3. 多分类回归（Softmax）

• 模型
  将线性组合通过 Softmax 函数映射为概率分布：

  \[p(y=k \mid x) = \frac{e^{\theta_k^T x}}{\sum_{j=1}^K e^{\theta_j^T x}} \]

• 损失函数（交叉熵损失）

  \[J(\theta) = -\sum_{i=1}^N \sum_{k=1}^K 1\{y^{(i)}=k\} \log p(y^{(i)}=k \mid x^{(i)}) \]

---

第二部分：神经元与感知机模型

1. 神经元模型（M-P模型）

• 结构
  输入加权求和后通过激活函数输出：

  \[y = f\left( \sum_{j=1}^n w_j x_j - \theta \right) \]

• 激活函数

  • 阶跃函数：
    \[f(x) = \begin{cases} 1, & x \geq 0 \\ 0, & x < 0 \end{cases}\]

  • Sigmoid 函数：
    \[f(x) = \frac{1}{1 + e^{-x}} \]

---

2. 感知机（Perceptron）

• 原理
  二分类模型，输出为符号函数：

  \[y = \text{sign}(w^T x) \]

• 损失函数
  误分类点到超平面的距离之和：

  \[L(w) = -\frac{1}{\|w\|} \sum y^{(i)} (w^T x^{(i)}) \]

• 训练方法
  通过误分类点更新权重（类似 Hebb 规则）：

  \[w_{k+1} = w_k + \eta y^{(i)} x^{(i)} \]

---

第三部分：多层感知机与BP算法

1. XOR问题与多层感知机

• 线性不可分问题
  单层感知机无法解决异或（XOR），需引入隐层。

• 三层感知机结构

  • 输入层 → 隐层（非线性激活） → 输出层。
  • 隐节点构造特征映射，输出层组合特征实现分类。

---

2. BP算法（误差反向传播）

• 核心思想
  通过链式法则计算梯度，逐层调整权重。

• 步骤

  1. 正向传播：计算网络输出。
  2. 反向传播：从输出层到输入层逐层计算误差梯度。
  3. 权重更新：梯度下降法优化参数。

• 损失函数
  均方误差或交叉熵。

---

3. 算法优缺点

• 优点

  • 通用性强，可逼近任意非线性函数。
  • 学习完全自主。

• 缺点

  • 非全局收敛，易陷入局部最优。
  • 学习率选择敏感。
  • 网络结构设计复杂（隐层数、节点数）。

---

4. 实践示例

• 数据集
  Fashion-MNIST（28x28 灰度图，10 类，6万训练+1万测试）。

• 代码示例（PyTorch数据加载）

  def load_data_fashion_mnist(batch_size, resize=None):
      trans = [transforms.ToTensor()]
      if resize:
          trans.insert(0, transforms.Resize(resize))
      trans = transforms.Compose(trans)
      mnist_train = torchvision.datasets.FashionMNIST(
          root="../data", train=True, transform=trans, download=True)
      mnist_test = torchvision.datasets.FashionMNIST(
          root="../data", train=False, transform=trans, download=True)
      return (DataLoader(mnist_train, batch_size, shuffle=True),
              DataLoader(mnist_test, batch_size, shuffle=False))