斜率优化

P2365 任务安排

解法

由于数据范围较小，考虑 \(O(n^2)\) 朴素动态规划。

设 \(dp_i\) 表示把前 \(i\) 个任务分成若干组完成的最小费用，显然有转移方程：

考虑前缀和优化，\(c_i=\sum\limits_{k=1}^ic_k\)，\(t_i=\sum\limits_{k=1}^it_k\)，则有：

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e3 + 5;
int n, s, a[N], b[N], dp[N];
signed main(){
	cin.tie(0)->sync_with_stdio(0);
	fill(dp, dp + N, 1e18);
	cin >> n >> s;
	for (int i = 1; i <= n; ++i){
		cin >> a[i] >> b[i];
		a[i] += a[i - 1], b[i] += b[i - 1];
	}
	dp[0] = 0;
	for (int i = 1; i <= n; ++i){
		for (int j = 0; j <= i; ++j){
			dp[i] = min(dp[i], dp[j] + (s + a[i] - a[j]) * (b[n] - b[j]));
		}
	}
	cout << dp[n];
	return 0;
}

P5785 [SDOI2012] 任务安排

解法

\(1\le n\le 3\times10^5\)，考虑使用斜率优化 dp。

先对原状态转移方程进行变形，省略 \(\min\)，有：

最终式子变为：

可以发现，这个形式很像一次函数，所以把 \(c_j\) 作为 \(x\)、\(dp_j\) 作为 \(y\) 建立平面直角坐标系，其中：\(k=t_i+s\)，\(b=dp_i-c_it_i-c_ns\)。

所以转移的 \(dp_j\) 一定在右下角的凸包顶点上，满足 \(j\) 左侧线段所在的直线的斜率小于等于 \(k\)，\(j\) 右侧线段所在的直线的斜率大于等于 \(k\)，则当前选择的 \(j\) 可用于转移 \(dp_i\)。

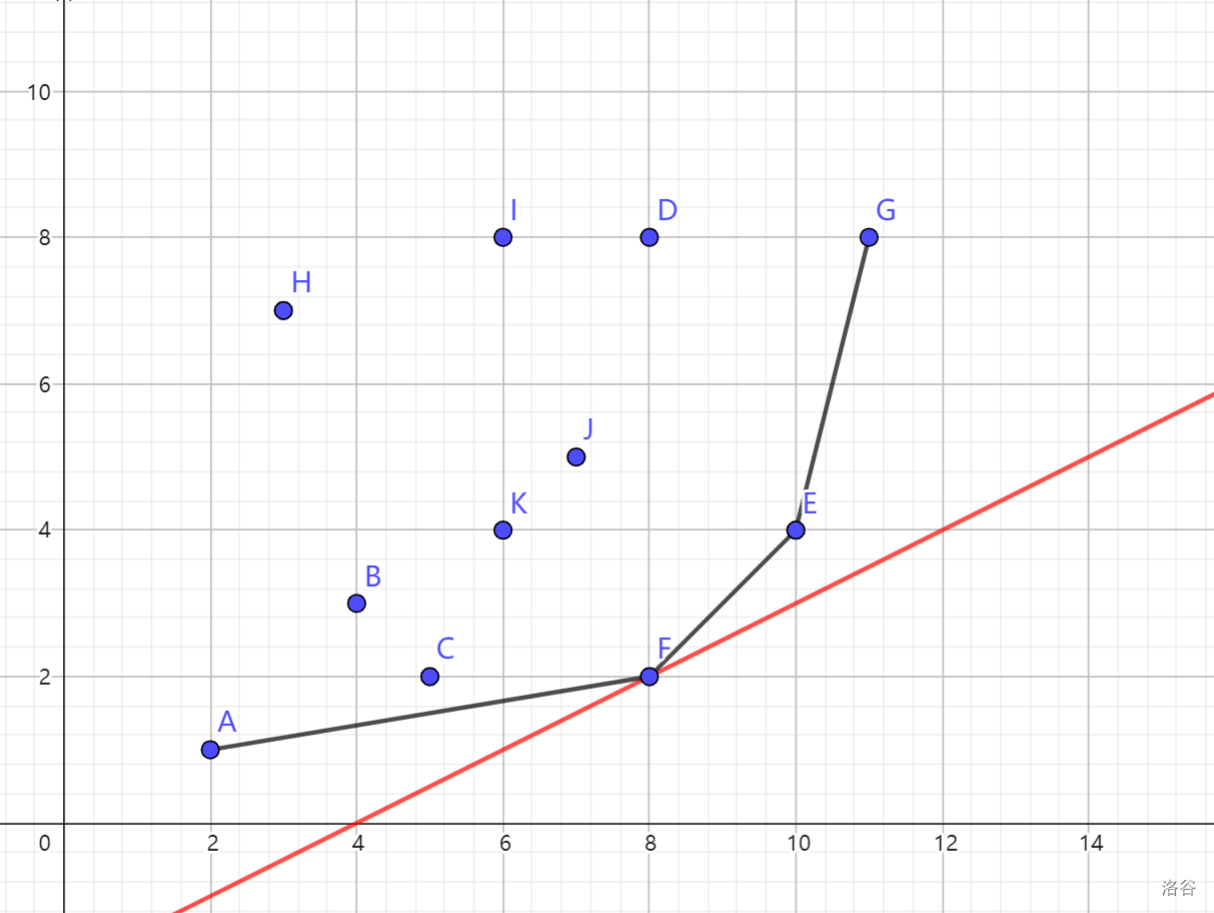
如图，此时点 \(F\) 即为可作为转移的点。

至于如何找点，我们动态维护了一个凸包，所以二分找点即可。由我们刚才的式子，还可以得到 \(dp_i=dp_j-(t_i+s)c_j + c_it_i + c_ns\)。

if (l == r)return q[l];
int L = l, R = r, mid;
while (L < R){
	mid = L + R >> 1;
	if (f[q[mid + 1]] - f[q[mid]] <= k * (c[q[mid + 1]] - c[q[mid]])){// 本行正常写法应为 (f[q[mid + 1]] - f[q[mid]]) / (c[q[mid + 1]] - c[q[mid]]) <= k，为了避免精度问题所以改为了乘法
		L = mid + 1;
	} else {
		R = mid;
	}
}
return q[L];

由于本题 \(c\) 单调不降，所以新加入的点一定在之前点的右侧（对于 \(\forall1\le j\le i\)，有 \(c_i\ge c_j\)），考虑下图情况：

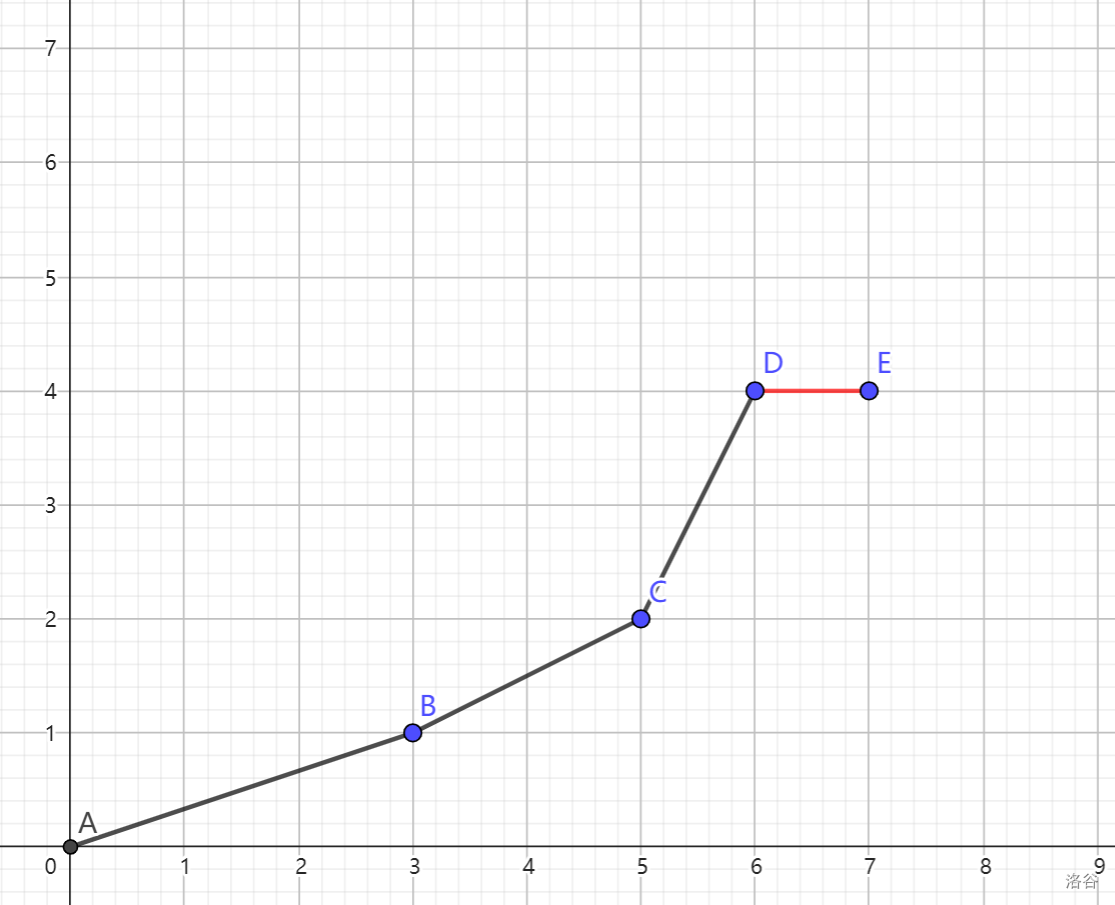
此时形成了一个凹包，每次添加点时，判断之前点有没有形成凹包即可，并且新加的点可能不对之前所有点产生影响，所以循环判断直到找不到凹包退出即可。

while (l < r && (f[q[r]] - f[q[r - 1]]) * (c[i] - c[q[r]]) >= (f[i] - f[q[r]]) * (c[q[r]] - c[q[r - 1]])){
	--r;
}

总时间复杂度 \(O(n\log n)\)，空间复杂度 \(O(n)\)。

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e5 + 5;
int n, s, l, r, t[N], c[N], f[N];
int q[N];
int search(int k){
	if (l == r)return q[l];
	int L = l, R = r, mid;
	while (L < R){
		mid = L + R >> 1;
		if (f[q[mid + 1]] - f[q[mid]] <= k * (c[q[mid + 1]] - c[q[mid]])){
			L = mid + 1;
		} else {
			R = mid;
		}
	}
	return q[L];
}
signed main(){
	cin.tie(0)->sync_with_stdio(0);
	cin >> n >> s;
	for (int i = 1; i <= n; ++i){
		cin >> t[i] >> c[i];
		t[i] += t[i - 1], c[i] += c[i - 1];
	}
	l = r = 1;
	for (int i = 1; i <= n; ++i){
		int k = s + t[i];
		int p = search(k);
		f[i] = f[p] - k * c[p] + t[i] * c[i] + c[n] * s;
		while (l < r && (f[q[r]] - f[q[r - 1]]) * (c[i] - c[q[r]]) >= (f[i] - f[q[r]]) * (c[q[r]] - c[q[r - 1]])){// 此行仍然是为了避免精度问题
			--r;
		}
		q[++r] = i;
	}
	cout << f[n];
	return 0;
} 

参考

题解：P10979 任务安排 2

DP优化之斜率优化小结