爱生气的书店老板 二维区域和检索 - 矩阵不可变 元素和为目标值的子矩阵数量

1052. 爱生气的书店老板

思路，把老板不生气时候的值都加起来，同时让当前值为零；
最后，按照最长时间滑动窗口，求解窗口最大值，与上值相加即可
int sum = 0;
for(int i = 0; i < customers.length; i++) {
if(grumpy[i] == 0) {
sum += customers[i];
customers[i] = 0;细节置零
}
}
int left = 0;
int right = minutes - 1;
int max = 0;
while(right < customers.length) {
int cur = 0;
for(int i = left; i <= right; i++) {
cur += customers[i];
}
max = Math.max(max, cur);窗口更新
left++;
right++;
}
return sum + max;

---

304. 二维区域和检索 - 矩阵不可变

求二维数组的前缀和
以[0,0] 为起点，当前位置为终点的矩阵之和

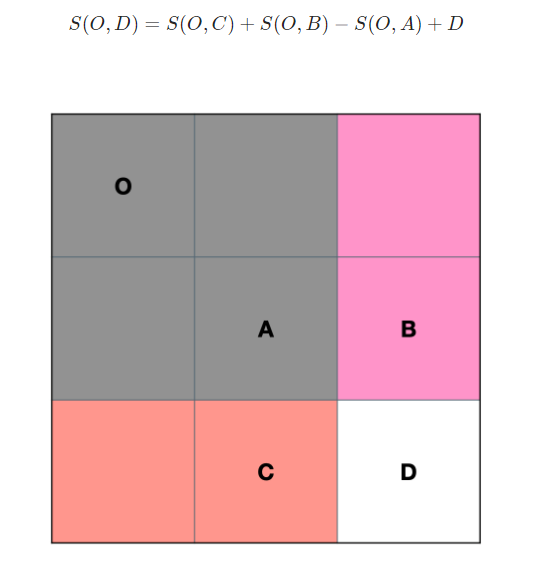
cur = new int[r + 1][c + 1];
for(int i = 1; i <= r; i++) {
for(int j = 1; j <= c; j++) {
cur[i][j] = cur[i - 1][j] + cur[i][j - 1] - cur[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}

---

1074. 元素和为目标值的子矩阵数量

求出前缀和
求右下方数值
int r = matrix.length, c = matrix[0].length;
int[][] sum = new int[r + 1][c + 1];
for(int i = 1; i <= r; i++) {
for(int j = 1; j <= c; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}

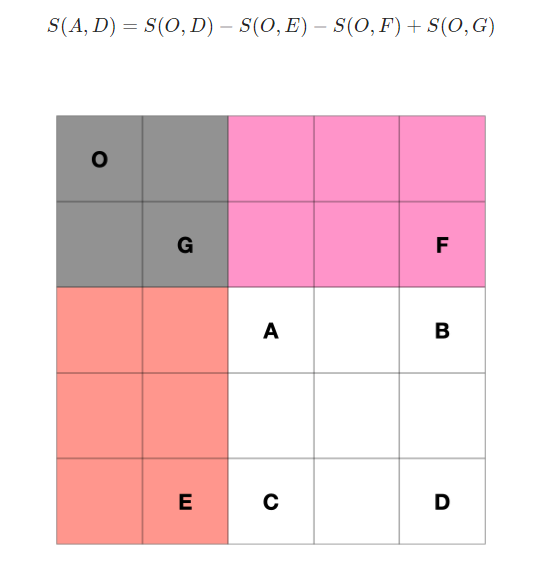
    int ans = 0;
    for(int i = 1; i <= r; i++) {
        for(int j = 1; j <= c; j++) {
            for(int x = 1; x <= i; x++) {
                for(int y = 1; y <= j; y++) {
                    if((sum[i][j] - sum[x - 1][j] - sum[i][y - 1] + sum[x - 1][y - 1]) == target) ans++;
                }
            }
        }
    }
    return ans;