IOI 2015 集训队作业选做

[USACO13OPEN Gold] Figure Eight
[USACO12OPEN Gold] Photo
[USACO09JAN Gold] Safe Travel
[CodeJam 2014 Finals C] Symmetric Trees
[CF356E] Xenia and String Problem
[CF343E] Pumping Stations
[CF338E] Optimize!
[CF338D] GCD Table
[CF335E] Counting Skyscrapers
[CF335F] Buy One, Get One Free
[CF332D] Theft of Blueprints
[CF331E1] Deja Vu
[CF331E2] Deja Vu
[CF325E] The Red Button
[CF325C] Monsters and Diamonds
[CF321D] Ciel and Flipboard
[CF319E] Ping-Pong

[USACO13OPEN Gold] Figure Eight

题面

暴力题。

枚举左右边界，从下往上递推，可以得到每一行这一左右边界向下最多扩展多少；同样从上往下递推可以得到向上最多扩展多少。

然后枚举中间那一行，按照左端点扫描线，用一个树状数组维护后缀 \(\max\)。复杂度 \(\mathcal{O}(n^3\log n)\)。

事实上有点蠢。只需要用 DP 数组记录向上 / 下最多扩展多少，并且向上的状态记录的值把它包含的区间的 DP 值全部取 \(\max\) 就行了。

卡空间用 short。

https://paste.ubuntu.com/p/fst6mP66FP/。

[USACO12OPEN Gold] Photo

题面

考虑 DP。设 \(f_i\) 表示最后一个有斑点的奶牛是 \(i\)，已经考虑的区间全部合法的方案数。

考虑 \(i\) 从 \(j\) 处转移而来，需要满足什么条件。不难发现其实就是 \([j+1,i-1]\) 不包含任何一个区间，并且 \([j,i]\) 没有被任何一个区间包含。这个可以记录右端点 \(< i\) 的区间中最靠右的左端点和右端点 \(\ge i\) 的区间中最靠左的左端点来找到。所以就是一个线段树优化转移的板子了。

https://paste.ubuntu.com/p/mjyhtk7MXC/。

[USACO09JAN Gold] Safe Travel

题面

考虑图的最短路树。因为这题给定的性质所以这棵最短路树是唯一的。

然后有一个观察，就是答案会且仅会经过一条非树边。证明考虑反证。

所以只需要把所有非树边 \((u,v,w)\) 拿出来，看它能更新多少个点的答案。

显然只会更新树上 \(u\to v\) 最短路径上的点，且这个更新的值为 \(dis_u+dis_v+w-dis_i\)，其中 \(i\) 为要更新的点。

并查集可以方便地维护这个过程。

https://paste.ubuntu.com/p/pvgsTcCgkB/。

[CodeJam 2014 Finals C] Symmetric Trees

题面

给一棵 \(N\) 个节点的树（\(N\le 10^4\)），每个节点有一个颜色（颜色最多 \(26\) 种），现在问它是不是对称的。对称的定义是，能把这棵树放在一个平面上，\(x =0\) 为对称轴，若在 \((x, y)\) 处有一点 \(v\)，那么在 \((−x, y)\) 处就一定有一个相同颜色的点 \(v'\)（如果 \(x =0\) 则它们为同一点），并且对于所有边 \((u, v)\)，\(u'\) 和 \(v'\) 间也一定有边。共\(T\) 组数据，\(T\le 100\)。

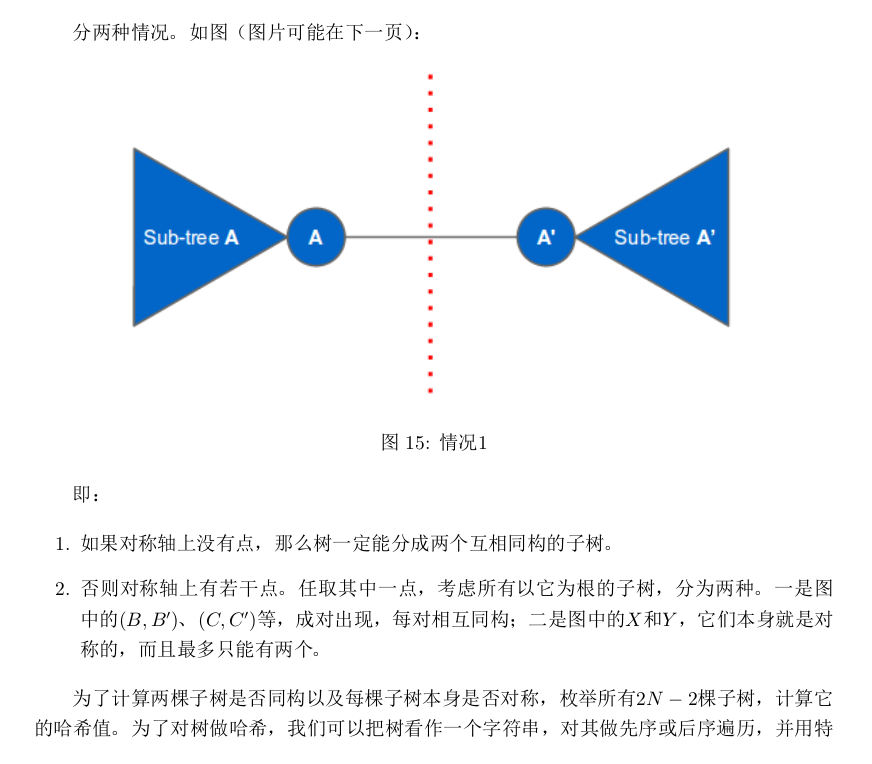
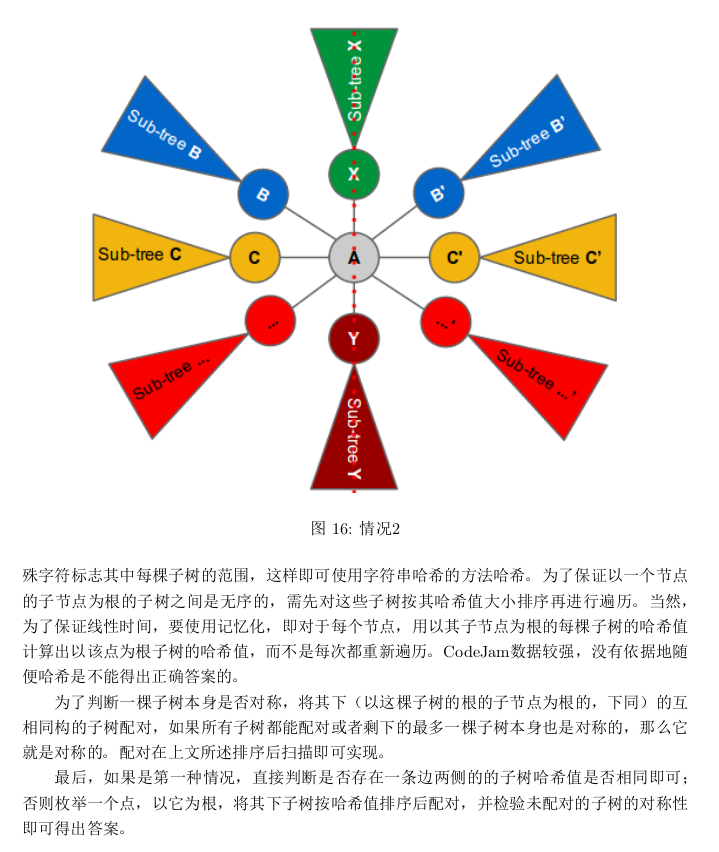
https://paste.ubuntu.com/p/ZbgCPDB3JZ/。

[CF356E] Xenia and String Problem

题面

https://www.luogu.com.cn/blog/chenggeorshidao/solution-cf356e。

https://paste.ubuntu.com/p/gK6SM3MXHQ/。

[CF343E] Pumping Stations

题面

最小割树的应用。

第一问就是最小割树边权和。

第二问的构造，可以考虑把边权最小的边断开，然后分成两个点集，对这两个点集分别求解再把它们直接接上就行了。

https://paste.ubuntu.com/p/jcs2Pmmx49/。

[CF338E] Optimize!

题面

考虑把所有 \(b_i\) 变成 \(h-b_i\)，然后将 \(b_i\) 从小到大排序，并将当前要匹配的 \(len\) 个 \(a_i\) 也从小到大排序，那么能匹配的条件就是 \(\forall i,a_i\ge b_i\)。

这个在值域上的表达就是，把 \(b_i\) 所在位置的权值看成 \(1\)，\(a_i\) 所在位置权值看成 \(-1\)，那么每个位置的前缀和 \(\ge 0\)。

离散化后线段树动态维护这个过程即可。

https://paste.ubuntu.com/p/DbHqCdfYNy/。

[CF338D] GCD Table

题面

显然 \(i\) 是 \(\operatorname{lcm}(a_1,a_2,\dots,a_k)\) 的倍数。

进一步的，如果有解那么 \(i\) 一定就是 \(\operatorname{lcm}(a_1,a_2,\dots,a_k)\)。

对于 \(j\) 的求解，我们可以列出 \(k\) 个同余方程，然后用 exCRT 得到解的值。

最后代入检验。

https://paste.ubuntu.com/p/6pqBfNfXGm/。

[CF335E] Counting Skyscrapers

题面

https://blog.csdn.net/zxyoi_dreamer/article/details/102313266。

https://blog.csdn.net/cqbzlydd/article/details/130871979。

https://paste.ubuntu.com/p/KNfS3Y8F9q/。

[CF335F] Buy One, Get One Free

题面

反悔贪心。

直接看洛谷题解。

那个“如果我们将 \(x\) 买下，然后来白嫖 \(a_i\)，那就可以相较于买下 \(a_i\)，净赚 \(2\times a_i\)”的意思，拿样例一来解释就是说，现在假如已经白嫖了两个 \(4\)，接下来扫到了两个 \(3\)，原则上这两个 \(3\) 都是不能白嫖的，这个反悔操作的意思就是把一个 \(4\) 不白嫖了，这样可以 \(5-4,5-3,4-3\) 配对。

https://paste.ubuntu.com/p/YMd7w7PzwC/。