2023 省选做题记录 1.0
- 1.3
- 1.4
- 1.5
- 1.6
- 1.8
- 1.9
- 1.10
- 1.11
- 1.12
- [洛谷 P1251] 餐巾计划问题(费用流)
- [洛谷 P2754] [CTSC1999] 家园 / 星际转移问题(最大流 + 分层图)
- [洛谷 P2761] 软件补丁问题(状压 + 最短路)
- [洛谷 P2770] 航空路线问题(费用流)
- [洛谷 P3356] 火星探险问题(费用流)
- [洛谷 P3358] 最长 k 可重区间集问题(费用流)
- [洛谷 P3357] 最长 k 可重线段集问题(费用流)
- [洛谷 P4009] 汽车加油行驶问题(最短路)
- [洛谷 P4011] 孤岛营救问题(BFS)
- [洛谷 P4012] 深海机器人问题(费用流)
- [洛谷 P4013] 数字梯形问题(费用流)
- [洛谷 P4016] 负载平衡问题(费用流)
- 1.13
- 1.15
- 1.16
- 1.17
1.3
[洛谷 P4717]【模板】快速莫比乌斯/沃尔什变换 (FMT/FWT)
要注意的一些地方:
-
二阶矩阵 \(A=\begin{bmatrix}a& b\\ c& d\end{bmatrix}\) 的逆矩阵为 \(A^{-1}=\frac{1}{ad-bc}\begin{bmatrix}d&-b\\-c&a\end{bmatrix}\)。
-
一堆集合要位运算卷积起来只需要对每一个集合分别 FWT,再把对应点值相乘,最后 IFWT 回来即可。
-
关于位矩阵:
- 满足 \(c_{i,j}c_{i,k}=c_{i,j\oplus k}\),其中 \(\oplus\) 可以是任何位运算符。
- 运算为或时,\(c_{i,j}=[i\&j=j]\),意义为子集和。
- 运算为与时,\(c_{i,j}=[i\&j=i]\),意义为超集和。
- 运算为异或时,\(c_{i,j}=(-1)^{|i\&j|}\)。
代码:https://pastebin.ubuntu.com/p/HMm5K3tYSm/。
[洛谷 P6097] 【模板】子集卷积
\(i|j=k\) 的条件可以看成是一个并卷积。
\(i\&j=0\) 的条件等价于 \(\mathrm{popcount}(i)+\mathrm{popcount}(j)=\mathrm{popcount}(k)\)。
因此再加一维表示 \(\mathrm{popcount}\) 就行了。
具体可见 https://www.luogu.com.cn/blog/EternalAlexander/solution-p6097。
代码:https://pastebin.ubuntu.com/p/pv9PB6k4cR/。
[HAOI2015] 按位或(min-max 容斥 + FWT)
首先需要了解 \(\min-\max\) 容斥:
它在期望下也成立。
那么我们就可以把问题变成求每个集合中有一个 \(1\) 出现的最早时间。
接下来介绍离散随机变量的几何分布:
对于一个离散随机变量 \(x\) 满足 \(P(x=k)=(1-p)^{k-1}p(k\in\mathbb{N}^+)\),其中 \(p\) 是一个常量,就称这个离散随机变量 \(x\) 服从参数 \(p\) 的几何分布。
其期望 \(E(x)=\sum\limits_{i=1}^{\infty}i(1-p)^{i-1}p=p\sum\limits_{i=1}^{\infty}i(1-p)^{i-1}\)。
如何求解?
\[\begin{aligned} s&=\sum\limits_{k}k(1-p)^{k-1}=1+2(1-p)+3(1-p)^2+\cdots\\ (1-p)s&=\sum\limits_{k}k(1-p)^k=(1-p)+2(1-p)^2+3(1-p)^3+\cdots\\ \therefore ps&=1+(1-p)+(1-p)^2+\cdots\\ (1-p)ps&=(1-p)+(1-p)^2+(1-p)^3+\cdots\\ p^2s&=1\\ s&=\frac{1}{p^2} \end{aligned} \]所以 \(E(x)=\frac{p}{p^2}=\frac{1}{p}\)。
回到本题中来。
对于一个集合 \(T\),\(\min(T)=k\) 的含义就是说在前 \(k-1\) 时刻里都没有取到 \(T\) 中的元素。即 \(P(\min(T)=k)=(1-P(S\oplus T))P(S\oplus T)^{k-1}\)。容易发现它服从系数为 \(1-P(S\oplus T)\) 的几何分布。所以可以套用期望公式直接求。
剩下的问题就是求解 \(P(S\oplus T)\) 了。其实就是求一个子集和,FWT 即可。
代码:https://pastebin.ubuntu.com/p/qHB37Dy5vS/。
1.4
[CF914G] Sum the Fibonacci(FWT + 子集卷积)
\(s_a|s_b\) 且 \(s_a\&s_b=0\) 的形式就是一个子集卷积。
\(s_d\oplus s_e\) 的形式是一个异或卷积。
然后整体上是一个与卷积。
一言不合直接卷起来就行了。
代码:https://pastebin.ubuntu.com/p/Zq2ZbpzH3w/。
[WC2018] 州区划分(枚举 + 并查集 + FWT + 子集卷积)
如果一个州合法,那么其必须满足其导出子图不连通或者导出子图中有度数为奇数的点。这个可以暴力 \(2^nn^2\) 并查集对每一个可能的点集都判断一遍。
设 \(f_s\) 表示已经选了集合 \(s\) 中的点的所有合法方案的满意度之和,\(W_s\) 表示点集 \(s\) 中所有点的 \(w_i\) 之和。
那么有转移:\(f_s=\frac{1}{W_s^p}\sum\limits_{s'\subsetneq s}f_{s-s'}W_{s'}^p[s'\text{ is valid}]\)。
容易发现这是一个子集卷积的形式。但由于这是类似于“自己卷自己”的形式,并且能贡献到 \(s\) 的都是它的真子集,所以按照 \(|s|\) 从小到大做卷积就行了。每次做完 \(|s|\) 相等的一些再乘上 \(\frac{1}{W_s^p}\) 的系数。也就是 cmd 所说的“半在线子集卷积”。
[洛谷 P5905]【模板】Johnson 全源最短路
Johnson 算法可以解决有负权的全源最短路问题。
其核心就是给每一个点赋予一个势能 \(h_i\),并将边权 \(w_{u,v}\) 变为 \(w_{u,v}+h_u-h_v\)。
怎么求这个 \(h_i\)?可以利用三角形不等式 \(h_v\le h_u+w_{u,v}\),使用 BF 算法进行 \(n-1\) 轮松弛求出。
具体的懒得写了,见 https://www.cnblogs.com/alex-wei/p/basic_graph_theory.html。
代码:https://pastebin.ubuntu.com/p/qvJhftqmgG/。
[CF1310D] Tourism(随机化 + 随机染色 + DP)
没有奇环 -> 二分图染色。
把所有点随机黑白染色,每次只走连接两个不同颜色的点的边,这样可以保证二分图的性质,即没有奇环。
考虑到 \(2\le k\le 10\),所以会经过的点只有不超过 \(10\) 个。可以做 \(\mathcal{O}(n^2k)\) 的暴力 DP 找出最短距离。
这样做一次的正确率是 \(\frac{1}{2^{k-1}}\)。那么只要做 \(4000\) 次就可以保证正确率至少为 \(1-(\frac{511}{512})^{4000}\) 了,这个概率还是非常大的。
代码:https://pastebin.ubuntu.com/p/nhxbBQSt6W/。
[POI2014] RAJ-Rally(拓扑排序 + multiset)
好题。至少给我整不会了。
先分别对正图和反图跑一遍拓扑排序,求出 \(ds_i\) 和 \(dt_i\) 分别表示以点 \(i\) 为起点的最长路和以点 \(i\) 为终点的最长路。
假设要删除 \(i\) 号节点,那么我们可以把剩下的节点分成 \(A\)、\(B\) 两部分,分别表示拓扑序比 \(i\) 小的点和拓扑序比 \(i\) 大的点构成的集合。删除 \(i\) 号节点后的最长路径可以有三种选择:全部在 \(A\) 中、全部在 \(B\) 中和跨过了 \(A\) 和 \(B\)。
全部在 \(A\) 中的贡献就是 \(dt_u(u\in A)\),全部在 \(B\) 中的贡献就是 \(ds_v(v\in B)\),跨过了 \(A\) 和 \(B\) 的贡献就是 \(ds_u+1+dt_v(u\in A,v\in B)\)。可以拿一个 multiset 来动态维护所有可能的贡献。
具体的,我们可以利用删除 \(i+1\) 号节点和删除 \(i\) 号节点的贡献的差别来对 multiset 进行插入删除。详细题解可见洛谷题解区。
代码:https://pastebin.ubuntu.com/p/j3GY9v54H9/。
1.5
Codeforces Global Round 24 A~G3
[洛谷 P5590] 赛车游戏(差分约束)
好题。至少这个转化很神奇。
考虑把限制从设置边权满足路径长度相等转化为设置长度去拟合边权的限制。
设 \(dis_i\) 表示 \(1\to i\) 的最短路径长度。只需要设置 \(w_{u,v}=dis_v-dis_u\) 就可以满足路径长度相等的条件。
所以就有限制 \(1\le dis_v-dis_u\le 9\),转化为 \(dis_u-1\ge dis_v\) 和 \(dis_v+9\ge dis_u\),差分约束求解即可。
代码:https://pastebin.ubuntu.com/p/gyZFY937SN/。
[CF241E] Flights(差分约束)
和上一题一模一样。
1.6
[联合省选 2021 A 卷] 矩阵游戏(差分约束 + 构造)
构造题的思考方式之一:调整法。更多详见 https://www.luogu.com.cn/blog/EternalAlexander/fu-xi-2-gou-zao-ti-di-sai-kao-fang-shi。
先把第一行、第一列全部设成 \(0\),然后可以求出一个不一定满足范围但肯定满足 \(b\) 矩阵的条件的 \(a\) 矩阵。
然后调整法,注意到只要给一行进行 \(+r_i ,-r_i,+r_i,\dots\) 的操作是不会改变 \(b\) 矩阵的。那么很容易有 \(a_{i,j}\leftarrow a_{i,j}+(-1)^{i+j}r_i+(-1)^{i+j}c_j\)。不难想到可以用差分约束解决。但是这样当 \(i+j\) 为偶数的时候会有 和约束,怎么办?很简单,只需要改成 \(a_{i,j}\leftarrow a_{i,j}+(-i)^{i+j+1}r_i+(-1)^{i+j}c_j\) 就行了。然后直接差分约束就行了。注意开 LL。
思路听起来很简单,但实际上想很困难。怎么办???还是做题太天马行空,没有固定章法。要改。
洛谷卡常。不知道为什么判负环的时候要改成判入队次数才能过,判最短路长度就过不了。
但是 LOJ 不卡。洛谷 too slow!
[洛谷 P4926] [1007]倍杀测量者(差分约束 + 二分)
把条件中的乘看成取 \(\log\) 之后加。然后就是正常的二分 + 差分约束了。如果有负环出现就合法。
初始确定分数的选手只需要连边 \((0,i,\log x)\) 和 \((i,0,-\log x)\)。
注意二分的上界。
代码:https://pastebin.ubuntu.com/p/NnXDn7dgFr/。
[POI2008] BLO-Blockade(割点)
题意其实就是要求断掉与一个点相连的所有边后形成的每个连通块的 \(sz(n-sz)\) 之和。
首先,如果要删的点不是割点,那么答案显然为 \(2(n-1)\)。
否则,由于无向图的 DFS 树的非树边都是返租边,那么我们可以像 DFS 求树的子树大小一样求出每个点 DFS 树上的子树大小,然后就可以方便地求出答案了。
代码:https://pastebin.ubuntu.com/p/kwfKwc6XjJ/。
[USACO06JAN] Redundant Paths G(割边)
题意即求出最少要加多少边使得整张图没有割边。
首先可以边双缩点,可以得到一棵树,树上所有边都是割边。
结论:答案即为这棵新树的叶子数量除以二上取整。
证明见 https://www.cnblogs.com/alex-wei/p/basic_graph_theory.html 4.6 例题 部分。
代码:https://pastebin.ubuntu.com/p/44w7w5nx8b/。
[CF51F] Caterpillar(Tarjan 缩点 + 直径的性质)
因为最终的毛毛虫不能包含重边,所以肯定是把图中的边双都缩成一个点,操作步数为边双中的点数 \(-1\)。然后图就变成了一个森林。把每棵树分开考虑,最后再用连通块个数 \(-1\) 次操作拼起来。
现在问题就变成:给定一棵树,要求通过合并操作将其变成一个毛毛虫的最少操作次数。
当我们确定主链之后,肯定是选择那些不在主链上的叶子作为挂在主链边上的节点。那么操作次数就是 点数 \(-\) 主链长度 \(-\) 主链外的叶子数量。
不难发现选择直径肯定最优。
证明见 https://www.cnblogs.com/alex-wei/p/basic_graph_theory.html 4.6 例题 部分。
记得特判只有一个节点的树。
代码:https://pastebin.ubuntu.com/p/rMnGg4tB6z/。
1.8
[ARC092F] Two Faced Edges(Tarjan 缩点 + bitset)
首先肯定是对整张图缩点。
然后对 SCC 之间的边和 SCC 内部的边分类讨论(设这条边是 \(u\to v\)):
- 对于 SCC 之间的边,强连通分量的数量改变当且仅当 \(u\) 能不经过 \(u\to v\) 这条边到达点 \(v\)。那么也就是要判断删去这条边后 \(u\) 还能否到 \(v\)。
- 对于 SCC 内部的边,强连通分量的数量改变当且仅当 \(u\) 在不经过 \(u\to v\) 这条边的情况下不能到达点 \(v\)。
- 具体证明:对于 SCC 内部任意一个点对 \((x,y)\),如果 \(x\to y\) 不必经 \(u\to v\) 这条边,那么反向之后不影响强连通性;否则由于 \(x\to v\) 必经 \(u\to v\),反向之后 \(x\) 就不能到达 \(v\),强连通性改变。
因此我们的目的就是要求出:对于每条边 \(u\to v\),\(u\) 能否在不经过这条边的情况下到达 \(v\)。
也就是说,设 \(u\) 的所有出边是 \(u\to v_1,v_2,\dots,v_k\),判断删去边 \(u\to v_j\) 之后 \(u\) 还能否到达 \(v_j\)。
考虑到如果 \(u\) 可以到达 \(v_j\),那么肯定只会经过一条另外的出边,并且剩下的边是一个前缀和一个后缀。所以我们就可以分别求出每个前缀和每个后缀可以到达的点,如果在扫到 \(u\to v\) 这条边的时候之前的边已经可以到达 \(v\),那么就标记 \(u\) 在删去 \(u\to v\) 这条边之后还可以到达 \(v\)。
前后缀分别扫一遍即可。
注意遍历图的时候需要使用 bitset,即如果当且访问过的点集为 \(vis\),当前点 \(u\) 的出边集合为 \(o_u\),那么遍历的时候就只需要利用 (~vis) & o[u] 中的信息,配合 _Find_first() 和 _Find_next(i)。
代码:https://pastebin.ubuntu.com/p/9NpZPShcBz/。
启示:序列去掉一个位置的信息可由前缀和后缀合并得到。
[POI2006] PRO-Professor Szu(Tarjan 缩点 + 拓扑排序)
题面有误,已知任意一栋住宅楼都存在至少一条前往主楼的路线 这句话是错误的。
如果一个 SCC 中有超过一个点,那么如果走进这个 SCC 就可以无限走下去。
所以说如果一个点可以经过一个点数 \(>1\) 的 SCC 或者某一个自环到达 \(n+1\),那么路线数肯定大于 \(36500\)。
这个可以通过建反图后拓扑排序来实现。只要不将点数 \(>1\) 或者存在自环的 SCC 入队即可。
最后,对于不能到达 \(n+1\) 的点,我们也可以通过建反图后将入度为 \(0\) 的不为 \(n+1\) 的点入队之后跑拓扑排序来找到。这个时候点数 \(>1\) 或者存在自环的 SCC 可以入队。
代码:https://pastebin.ubuntu.com/p/Pv4G5W9wF5/。
[NOI2021] 庆典(Tarjan 缩点 + 拓扑排序 + 树链剖分求链并)
题目里那个奇怪的条件等价于:缩点之后去掉前向边可以形成一棵外向树。那么可以先把这棵树建出来。具体的就是只保留拓扑序最大的边。
然后对于所有给定的 \(2(k+1)\) 个城市端点,若 \(i\) 可以到达 \(j\)(即 \(i\) 是 \(j\) 的祖先),并且 \(s\) 可以到达 \(i\)、\(j\) 可以到达 \(t\),那么 \(i\) 到 \(j\) 的这一条链就都可以被经过。这个可以通过枚举 + dfs 解决。
求链并可以用树剖。具体的就是把一条整链拆成若干条重链或者重链的一部分,设这样拆开之后的每条链为 \([l_i,r_i]\),将它们按照 \(l_i\) 从小到大排序,然后就是一个线段覆盖了。可以预处理前缀和解决。
1.9
[洛谷 P8863]「KDOI-03」构造数组(DP)
把问题看成,每个位置上有 \(b_i\) 个空位,每次选择两个不同位置上的空位填掉,也即有 \(\frac{\sum b_i}{2}\) 个槽,每个槽里有两个位置,每个位置上填一个数,且第一个位置上的值比第二个位置上的值小,每个数的出现次数为 \(b_i\),求方案数。
考虑从前往后 DP。设 \(s_i\) 为前 \(i\) 个数的 \(b\) 之和,\(f_{i,j}\) 表示前 \(i\) 个位置中,已经有 \(j\) 个槽填满了配对的方案数。不难发现有 \(s_i-2j\) 个槽还要填第二个位置,有 \(\frac{s_n}{2}-(s_i-2j)-j\) 个槽没有填任何数。
转移就枚举当前位置有多少个数填到第二个位置里,系数就是一些组合数,都比较好推,此处略去。
代码:https://pastebin.ubuntu.com/p/CvKgvdGvQP/。
[洛谷 P8456]「SWTR-8」地地铁铁(圆方树)
正难则反,考虑求出 \(\binom{n}{2}-\) 不合法的点对数量。
将所有不合法点对 \((u,v)\) 分类:
- \(u,v\) 之间只有只出现
D的简单路径; - \(u,v\) 之间只有只出现
d的简单路径; - \(u,v\) 之间只有只出现
D和只出现d的简单路径。
对于第一种情况,我们可以考虑建出圆方树,把所有对应点双内有 d 边的方点封锁掉(即删去其对应的所有出边),然后并查集即可。每个连通块内的点对都是满足条件的。第二种情况同理。
难点在于第三种情况。首先可以确定的是所有满足第三种情况的 \(u,v\) 都只会在同一个点双内出现。
证明:如果 \(u,v\) 不在同一个点双内,那么圆方树上 \(u\to v\) 的路径一定会经过一个圆点,也即 \(u\to v\) 的所有路径都会经过这个圆点。不难发现通过调整在这个圆点处的走向一定可以使得 \(u\to v\) 的一条路径上同时存在
D和d。因此 \(u,v\) 在同一个点双内。
那么我们将每一个点双分开考虑。显然若点双内所有边的权值都一样那么这个点双就没有贡献。
否则,点双内一定有一个点 \(u\) 满足与 \(u\) 相连的边中既有标 D 的,也有标 d 的。不妨设存在边 \((u,x_0)\) 标 d,\((u,y_0)\) 标 D。
接下来,我们断言:对于任意 \(x,y\),如果 \(x,y\) 和 \(u\) 在同一个点双内,并且 \(x\ne y,x\ne u,y\ne u\),那么 \(x\to y\) 一定存在一条路径同时经过边 \((u,x_0)\) 和 \((u,y_0)\)。证明见洛谷题解区。
所以说一个点双最多只有可能存在一个满足第三个条件的点对。统计一下每个点双内有两种权值的出边的点数是否为 \(2\) 就行了。
代码:https://pastebin.ubuntu.com/p/VbJvTHfXyp/。
[洛谷 P7771]【模板】欧拉路径(欧拉回路)
字典序最小只需要对出边排序即可。
剩下的就是无脑 dfs,以及注意当前弧优化。
代码:https://pastebin.ubuntu.com/p/f8RnhSRqhm/。
[POI2011] SMI-Garbage(欧拉回路)
题意大概就是说钦定有些边只能走奇数次,有些边只能走偶数次,要求选择若干个环使得每条边被覆盖的次数满足奇偶限制。
容易发现覆盖偶数次的边一定可以通过某些等价操作使得它们没有被覆盖。
所以问题就变成保留若干条边,用若干个环覆盖每条边恰好一次。直接跑欧拉回路然后拆环即可。
具体就是维护每个点是否在当前序列中,当再次遇到某个在序列中出现的节点的时候就将这个环拿出来。
代码:https://pastebin.ubuntu.com/p/v5Hkpx2Jbv/。
[POI2006] LIS-The Postman(欧拉回路 + 链表 + 构造)
将一定要相邻出现的边缩成一条链,如果缩完之后的形态不是一条链就说明无解。
然后直接跑欧拉回路就是了。
说起来简单,实现起来细节超级多,吐了。
代码:https://pastebin.ubuntu.com/p/GjbJ25FzXb/。
1.10
[ABC077D / ARC084B] Small Multiple(同余最短路)
这个第一步就很神奇。
注意到每个正整数都可以由 \(1\) 通过若干次 \(+1/\times 10\) 得到。那么就可以由每个点 \(i\) 向 \((i+1)\bmod n\) 连长度为 \(1\) 的边,向 \(10i\bmod n\) 连长度为 \(0\) 的边。最后到达 \(0\) 的最短路就是答案。
直接跑 01BFS/SPFA/Dijkstra 即可。
代码:https://pastebin.ubuntu.com/p/9Vkg5dDTHK/。
无限背包问题考虑同余最短路。
[NOI2017] 游戏(2-SAT + 枚举)
因为这个 \(d\) 很小,所以我们可以暴力枚举每一个 x 实际上是什么。不难发现只要枚举两个字母就可以覆盖所有情况。
接下来就是一个裸的 2-SAT 了。每个地图拆成两个点,分别表示这个地图上可以使用的两种赛车。直接连边就行。
注意如果 \(i\) 不能选择 \(h_i\),那么这个限制就相当于没有;如果 \(j\) 不能选择 \(h_j\),那么 \(i\) 也就不能选择 \(h_i\)。钦定某个 bool 变量的值为 \(p\) 等价于由 \(\lnot p\) 向 \(p\) 连边。
[APIO2018] 铁人两项(圆方树 + 拆贡献)
将题目转化成:先选择两个点 \(s,f\),再在所有可能出现在 \(s\to f\) 的路径中的点中选择一个作为 \(c\),问方案数。
首先考虑确定了 \(s\) 和 \(f\) 之后,选择 \(c\) 的方案数就是圆方树上 \(s\to f\) 路径中所有方点所代表的点双的点集的并的大小。这个可以通过将方点权值设为所代表的点双大小、圆点权值设为 \(-1\),然后求 \(s\to f\) 的路径和计算。
考虑换一种方式求和,即考虑每个点的点权会在多少对 \(s\) 和 \(f\) 中被算入。这个可以正难则反,用总方案数减去这个点的每个子树中选择 \(s\) 和 \(f\) 的方案数。
注意图有可能不连通。
[SDOI2018] 战略游戏(圆方树 + 虚树)
先建出圆方树。再把所有给出点的虚树建出来。然后就相当于统计虚树里除了给出点的圆点个数。
这个在加边的时候根据深度差和两个端点是圆点/方点可以讨论得出。
注意清空!!!!!!!!!
[COI2007] Policija(圆方树)
第二个问题很简单,判断 \(C\) 是否在圆方树上 \(A\to B\) 的路径上就行了。可以用距离判断。也可以直接分讨。
对于第一个问题,显然只有桥会改变两点的连通性,而这在圆方树上的体现是点双大小为 \(2\) 并且对应的方点在 \(A\to B\) 的路径上。也可以直接判断。
代码:https://paste.ubuntu.com/p/F6YM48bDrV/。
[HNOI2012] 矿场搭建(圆方树)
题目要求即为标最少的关键点,使得删去某个点后形成的每一个连通块中都有至少一个关键点。
容易发现删去割点的情况包含了删去非割点的情况。所以只需要对图中没有割点的情况单独讨论一下就行(最少选择 \(2\) 个点,方案数为 \(\binom{|V|}{2}\))。
接下来套路建出圆方树。首先剔除所有非割点(即圆方树上的叶子)。
给出结论:最少选择点数为圆方树剔除所有非割点之后形成的新树中叶子(也即度数为 \(1\) 的方点)个数。设这些叶子对应的点双大小为 \(s_1,s_2,\dots,s_k\),那么第二问答案即为 \(\prod\limits_{i=1}^k (s_i-1)\)。
证明见 https://www.cnblogs.com/alex-wei/p/high_level_graph_theory.html 3.4 例题 V。懒得写了。
代码:https://paste.ubuntu.com/p/DVkJkb3pNp/。
Codeforces Round #843 (Div. 2) A~E
1.11
2023.1.11 考试
T1
题面:

题解:
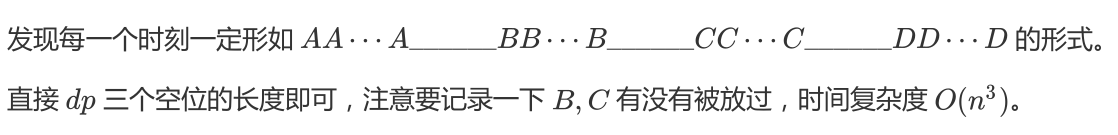
考虑倒推。如果 BC 都有那么会有三个空连续段;如果只有 BC 中的一种就只有两个空连续段;如果 BC 都没有就只有一个空连续段。根据这三种状态分别 DP 即可。转移的时候枚举下一个不同字母出现的位置。具体看代码。
代码:https://paste.ubuntu.com/p/gspBRGZG6K/。
T2
题面:

题解:

写的很详细了!
代码:https://paste.ubuntu.com/p/pzYSKfYSrc/。
T3
题面:

题解:

std:https://paste.ubuntu.com/p/trQ4byxBYd/。
1.12
[洛谷 P1251] 餐巾计划问题(费用流)
拆点。将每天拆成白天和晚上两个点。不然有可能会将干净的餐巾当成脏的餐巾一起流。
由源点向每天晚上的的点连流量为 \(r_i\),费用为 \(0\) 的边;由每天早上的点向汇点连流量为 \(r_i\),费用为 \(0\) 的边。代表这一天的餐巾消耗情况。
由源点向每天早上的点连流量为 \(\infty\),费用为 \(p\) 的边。代表购买餐巾。
然后由每天晚上的点分别向后 \(m\) 天和后 \(n\) 天早上的点连边,流量为 \(\infty\),费用为洗餐巾的费用;还要向后一天晚上的点连边,流量为 \(\infty\),费用为 \(0\),代表延期送洗。
跑最小费用最大流即可。
代码:https://paste.ubuntu.com/p/hDYk62vNjv/。
[洛谷 P2754] [CTSC1999] 家园 / 星际转移问题(最大流 + 分层图)
一艘太空船所停靠的站点随着时间的变化而变化,这启发我们使用 分层图 来刻画整个星际转移过程。
最重要的一点是,分层图的题目数据范围一般很小。
枚举答案 \(t\)。建立 \(t\) 层点,每一层有 \(n\) 个点。每一层的点向下一层对应的点连流量为 \(\infty\) 的边,表示可以停留。
同时,第 \(i\) 时刻第 \(j\) 个太空船所在的位置向第 \(i+1\) 时刻第 \(j\) 个太空船所在的位置连流量为 \(h_j\) 的边。表示一次转移。
注意地球和月球不需要每一层新建点。
在加入一层点之后的残量网络上跑最大流,如果和之前的最大流相加 \(\ge k\) 就说明答案是当前枚举到的天数。
代码:https://paste.ubuntu.com/p/cnRsqdFyFq/。
[洛谷 P2761] 软件补丁问题(状压 + 最短路)
观察到 \(n\) 很小,所以我们可以把所有可能的错误集合状压下来,每次看能否用一个补丁。
显然这是一个最短路模型,但是并不需要显式建图。SPFA 即可。
代码:https://paste.ubuntu.com/p/ZQXbx4y5Qp/。
[洛谷 P2770] 航空路线问题(费用流)
将题意转化为选择两条从起点到终点的不交路径。
看到这种限制点的经过次数,肯定首先想到拆点。
将每个点拆成两个点 \(i_{in}\) 和 \(i_{out}\),称之为入点和出点。对于起点和终点,入点向出点连流量为 \(2\) 的边(因为它们可以经过两次);其他点就连流量为 \(1\) 的边。
然后对于一条边 \((u,v)\),由 \(u_{out}\) 向 \(v_{in}\) 连一条流量为 \(1\) 的边,表示一条边只能经过一次。
因为还要途径城市最多,所以将除了起点和终点的所有点入点和出点之间的连边设置一个费用 \(1\),跑最大费用最大流即可。
代码:https://paste.ubuntu.com/p/CQ764FGpbq/。
[洛谷 P3356] 火星探险问题(费用流)
拆点。如果 \(a_{i,j}=2\) 就连一条流量为 \(1\)、费用为 \(1\) 的边和一条流量为 \(n-1\)、费用为 \(0\) 的边;\(a_{i,j}=0\) 就连一条流量为 \(n\)、费用为 \(0\) 的边。位置相邻且两个点都可以走的话就连流量为 \(n\)、费用为 \(0\) 的边。
跑最大费用最大流。
输出方案可以记录每个点向下和向右分别走了多少。
代码:https://paste.ubuntu.com/p/Zm4MCzSq3M/。
[洛谷 P3358] 最长 k 可重区间集问题(费用流)
一个合法的 \(k\) 可重区间集一定可以用不超过 \(k\) 条链将所有区间串起来,满足链上相邻区间不交。
比较显然的想法还是拆点,入点向出点连流量为 \(1\)、费用为 \(r-l\) 的边;如果区间 \(i\) 和 \(j\) 不交那么由 \(i\) 的出点向 \(j\) 的入点连流量为 \(1\)、费用为 \(0\) 的边。\(S\) 向所有入点连边,所有出点向 \(T\) 连边,\(T\) 向 \(T'\) 连流量为 \(k\)、费用为 \(0\) 的边限制 \(k\) 可重的条件。最大费用最大流即是答案。
但这样边数是 \(\mathcal{O}(n^2)\) 的。不够优秀。
考虑离散化之后把坐标看成点。设离散化后的坐标为 \(x_1,x_2,\dots,x_m\),那么令 \(x_0=0\),\(\forall 0\le i<m\),由 \(x_i\) 向 \(x_{i+1}\) 连流量为 \(k\)、费用为 \(0\) 的边。对于一条线段 \(i\),如果它的坐标离散化之后对应的点为 \(x_l,x_r\),那么由 \(x_l\) 向 \(x_r\) 连流量为 \(1\)、费用为线段 \(i\) 的长度的边。
边数为 \(\mathcal{O}(n)\),可以通过此题。
代码:https://paste.ubuntu.com/p/HfSPSY54ch/。
[洛谷 P3357] 最长 k 可重线段集问题(费用流)
和上一题差不多。只是需要考虑 \(x_0=x_1\) 的情况:如果还是按照上面那样建图就会忽略这种线段的影响。
所以考虑拆点:每个坐标拆成入点和出点,入点向出点连流量为 \(k\)、费用为 \(0\) 的边。
如果 \(x_0\ne x_1\) 就由 \(x_0\) 对应的出点向 \(x_1\) 对应的入点连边;否则就由 \(x_0\) 对应的入点向出点连边,流量为 \(1\)、费用为线段长度。该坐标的出点向下一个坐标的入点连流量为 \(k\)、费用为 \(0\) 的边。
最大费用最大流即可。
代码:https://paste.ubuntu.com/p/PCczDgz22k/。
[洛谷 P4009] 汽车加油行驶问题(最短路)
设 \(f_{i,j,k}\) 表示走到了坐标 \((i,j)\),剩余油量为 \(k\) 的最小费用。
直接跑 Dijkstra 即可。分这几种情况松弛就行。
代码:https://paste.ubuntu.com/p/JCvmbt2rr3/。
[洛谷 P4011] 孤岛营救问题(BFS)
设 \(f_{i,j,s}\) 表示到达 \((i,j)\) 已有的钥匙集合为 \(s\) 的最短时间。
BFS 转移即可。
代码:https://paste.ubuntu.com/p/2XyJym38fT/。
[洛谷 P4012] 深海机器人问题(费用流)
和火星探险问题一样的建图方法。
然后跑最大费用最大流。
代码:https://paste.ubuntu.com/p/gyg5Y9H8tb/。
[洛谷 P4013] 数字梯形问题(费用流)
拆点。
通过限制入点和出点之间的流量来控制在顶点处的相交情况;通过限制边的流量来控制在边上的相交情况。
最大费用最大流。
代码:https://paste.ubuntu.com/p/W5Tq7djwpc/。
[洛谷 P4016] 负载平衡问题(费用流)
先算出最后这 \(n\) 个仓库的库存 \(avg\)。
对于 \(a_i>avg\),连边 \((S,i,a_i-avg,0)\);对于 \(a_i<avg\),连边 \((i,T,avg-a_i,0)\)。相邻的连边 \((+\infty,1)\)。
最小费用最大流。
代码:https://paste.ubuntu.com/p/GtNwbGYRMy/。
1.13
[NOI2009] 植物大战僵尸(最大权闭合子图 + 拓扑排序)
显然我们可以根据植物之间的保护关系建一张图。即如果植物 \(i\) 保护植物 \(j\),那么连边 \(i\to j\)。注意隐藏条件:右边的植物保护左边的植物。
然后跑一遍拓扑排序,能遍历到的节点说明不在某个环内,可以得到它的 Score。
对于所有遍历到的节点在反图上跑最大权闭合子图。即:如果点权 \(w_i>0\),那么连边 \((S,i,w_i)\);如果 \(w_i<0\),连边 \((i,T,-w_i)\);对于一条边 \((u,v)\),因为选了 \(u\) 就要选 \(v\),所以连边 \((u,v,\infty)\)。所有正权值之和减去最小割就是答案。
代码:https://paste.ubuntu.com/p/PGpQrGm4Jk/。
[ZJOI2010] 网络扩容(费用流)
第一问直接跑流量为 \(c\)、费用为 \(0\) 的费用流,最大流量就是答案。
对于第二问,新建流量为 \(k\)、费用为 \(w\) 的边,并且限制最大流量为 \(k\),最小费用就是答案。
代码:https://paste.ubuntu.com/p/tzkyC2SYGH/。
[洛谷 P5192]【模板】有源汇上下界最大流(上下界网络流)
对每一天和每个人建两排点。
源点向每一天连流量为 \([0,D_i]\) 的边;每一天向对应的人连流量为 \([L,R]\) 的边;每个人向汇点连流量为 \([G_i,\infty)\) 的边。
跑有源汇上下界最大流即可。判断无解的条件是超级源点 \(S'\) 的出边全部满流。
代码:https://paste.ubuntu.com/p/dBNPsNG7MZ/。
1.15
[洛谷 P4843] 清理雪道(上下界网络流)
\(S\to i\to T\) 连流量为 \([0,+\infty]\) 的边;对于原图中的边连流量为 \([1,+\infty]\) 的边。跑有源汇上下界最小流。
代码:https://paste.ubuntu.com/p/t5jsfRwH93/。
[洛谷 P4553] 80 人环游世界(有源汇上下界最小费用可行流)
新建点 \(s,s',t\),对每个国家拆点,连边如下:
- \(s\to s': ([m,m],0)\),即流量范围为 \([m,m]\),费用为 \(0\)。下同。
- \(s'\to i:([0,m],0)\)。
- \(i\to i+n:([v_i,v_i],0)\)。
- \(i+n\to t:([0,m],0)\)。
- 如果存在边 \((i,j)\),那么连边 \(i+n\to j:([0,m],g_{i,j})\)。
跑一遍有源汇上下界最小费用可行流即可。
代码:https://paste.ubuntu.com/p/qyyMgZv4VC/。
1.16
[THUPC2022 初赛] 分组作业(最小割 + 集合划分模型)
考虑集合划分模型。
对于每个人,如果他与 \(S\) 相连就表示他选择“愿意”,与 \(T\) 相连就表示他选择“不愿意”。因此连边 \((S,i,d_i)\)、\((i,T,c_i)\)。
难点是喜欢关系怎么处理。
考虑把“合作”与“愿意”分开考虑,即对于每个组新建一个虚点表示是否合作。如果组 \(j\) 合作就与 \(S\) 相连,否则与 \(T\) 相连。
如果某个人 \(i\) 不同意,那么肯定不能合作。所以组 \(j\) 向其中的人 \(i\) 连一条流量为 \(+\infty\) 的边,表示如果组 \(j\) 合作且 \(i\) 不同意那么代价为 \(+\infty\)。
如果 \(A\) 对应的组和 \(T\) 相连,且 \(B\) 和 \(S\) 相连,就会有 \(a_i\) 的代价产生,那么由 \(B\) 对应的点向 \(A\) 对应的组连流量为 \(a_i\) 的边;如果 \(A\) 和 \(T\) 相连,且 \(B\) 对应的组和 \(S\) 相连,就会有 \(b_i\) 的代价产生,那么由 \(B\) 对应的组向 \(A\) 对应的点连流量为 \(b_i\) 的边。
图的最小割就是答案。
代码:https://paste.ubuntu.com/p/jzJW5T3hS2/。
[CF103E] Buying Sets(最小割 + 最大权闭合子图)
将权值取反,变成要求选择的子集权值和最大,输出的时候再取反回来。
如果没有 \(|\mathrm{N}(S)|=|S|\) 的限制,那么就是一个裸的最大权闭合子图。
注意到题目这个 \(|\mathrm{N}(S)|\ge |S|\) 的限制很强,于是考虑可以进行一些什么操作使得 \(|\mathrm{N}(S)|>|S|\) 的情况不会被考虑到。
将每个点的权值减去 \(+\infty\),将每个子集的权值加上 \(+\infty\),再去跑最大权闭合子图就可以得到答案了。原因是当 \(|\mathrm{N}(S)|>|S|\) 的时候,选择的点数会比选择的集合数多,至少会选择一条 \(+\infty\) 的边割掉。
代码:https://paste.ubuntu.com/p/4Jg7sYXQgg/。
1.17
[省选联考 2022] 学术社区(网络流 + 欧拉回路)
好题。部分分能很好地启发正解。
特殊性质 ABC
题面中的“消息”具有明显的指向性,并且如果把人看成点,那么消息就是连接人的边。这启发我们从图论建模的角度去思考这道题。
对于每条楼下型消息 A B louxia,连边 \(B\to A\)。那么所有符合实际情况的消息肯定是形成了若干条从某条学术消息开始的链。
建立一个虚点 \(S\),对于一条 A 发出的学术消息,连边 \(S\to A\)。对于一个出度 \(out_i\) 比入度 \(in_i\) 小的点 \(i\),会有 \(in_i-out_i\) 条消息在这里结尾,因此连 \(in_i-out_i\) 条 \(i\to S\) 的边。
跑一遍欧拉回路,输出的时候记得忽略新加入的边。
特殊性质 AC
注意到因为之前有特殊性质 B,所以不会存在 \(in_i<out_i\) 的情况,否则就会有消息不符合实际情况。
那么现在会出现这种情况,考虑怎么处理。不难发现这样一定会有 \(out_i-in_i\) 条消息不符合实际情况。我们只需要对于 \(in_i<out_i\) 的点连 \(out_i-in_i\) 条 \(S\to i\) 的边,再跑欧拉回路就能满足条件。经过这种边的下一条边就是不符合实际情况的。
特殊性质 BC
考虑最终每条链的形态,一定是形如 若干条楼上型消息 + 一条学术消息 + 若干条楼下型消息。
那么就考虑分层图,将楼上型消息和楼下型消息分开到两张图上考虑。设楼上型消息在图 \(G_1\) 上考虑,楼下型消息在图 \(G_2\) 上考虑。对于 A B loushang,在 \(G_1\) 里连边 \(A\to B\);对于 A B louxia,在 \(G_2\) 里连边 \(B\to A\);对于一条 A 发出的学术消息,从 \(G_1\) 中的点 \(A\) 向 \(G_2\) 中的点 \(A\) 连边。然后建立一个虚点 \(S\) 来保证每个点入出度平衡,跑欧拉回路。
特殊性质 C
现在并不是所有消息都满足条件。考虑如何选择舍弃的边,即把某条楼上型消息或楼下型消息变成学术消息。
首先考虑一下答案的下界。对于 \(G_1\) 中 \(in_i>out_i\) 的点会有 \(in_i-out_i\) 条消息不符合实际情况;\(G_2\) 中 \(in_i<out_i\) 的点会有 \(out_i-in_i\) 条消息不符合实际情况。所以下界就是所有非学术消息的数量减去上述两种情况。我们称这两种情况为 某个点不合法。
接下来考虑怎么提升答案的下界。如果舍弃一条形如 A B loushang 的消息,那么 \(G_1\) 中 B 的入度会 \(-1\),\(G_2\) 中 A 的入度会 \(+1\),这个时候如果 \(G_1\) 中的 B 和 \(G_2\) 中的 A 都是不合法的点,答案下界就可以 \(+1\);同理,如果舍弃一条形如 A B louxia 的消息,就考虑 \(G_1\) 中的 A 和 \(G_2\) 中的 B。
这是一个匹配问题,考虑网络流,使用类似二分图的建模方式解决:建两排点分别表示 \(G_1\) 中的 \(n\) 个点和 \(G_2\) 中的 \(n\) 个点,由源点 \(S\) 向 \(G_1\) 中 \(in_i>out_i\) 的点连流量为 \(in_i-out_i\) 的边;由 \(G_2\) 中 \(in_i<out_i\) 的点向汇点 \(T\) 连流量为 \(out_i-in_i\) 的边;对于形如 A B loushang 的消息,由 \(G_1\) 中的 B 向 \(G_2\) 中的 A 连边;对于形如 A B louxia 的消息,由 \(G_1\) 中的 A 向 \(G_2\) 中的 B 连边。最大流大小就是答案下界可以增加的量。
考虑构造方案。利用残量网络找到被舍弃的消息,将它们看成学术消息,然后使用特殊性质 BC 的建图方法跑欧拉回路。
正解
对于特殊性质 C 中提到的这两条消息,不难发现将它们放在一起肯定是不劣的。所以将这两条消息拼起来变成一条学术消息,按照上面的方法处理就行了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号