hello-algo

复杂度分析

迭代与递归

  • 函数返回前上下文存储在栈帧空间，故递归比迭代耗费更多内存空间
  • 递归调用函数有额外开销，故递归时间效率也更低

迭代

  • while循环更灵活，for循环更简洁

尾递归和正常递归

image

image

  • 尾递归会被编译器优化，空间效率相当于迭代！！！原因是尾递归无需保存上下文，正常递归需保存上一层递归的上下文
/* 普通递归 */
int Recursion(int i)
{
    if (i == 1) return 1;
    int res = Recursion(i - 1);
    return i + res;
}

/* 尾递归，将存储结果的变量res置为参数 */
int tailRecur(int i, int res)
{
    if (i == 0) return res;
    return tailRecur(n - 1, res + n);
}
int func()
{
    int res = 0;
    return tailRecur(5, res); //计算1--5的和，存储在res中
}
  • 尾递归本质就是直接return func() 好处是递的时候计算，归的时候一路返回某个确定的数

递归树

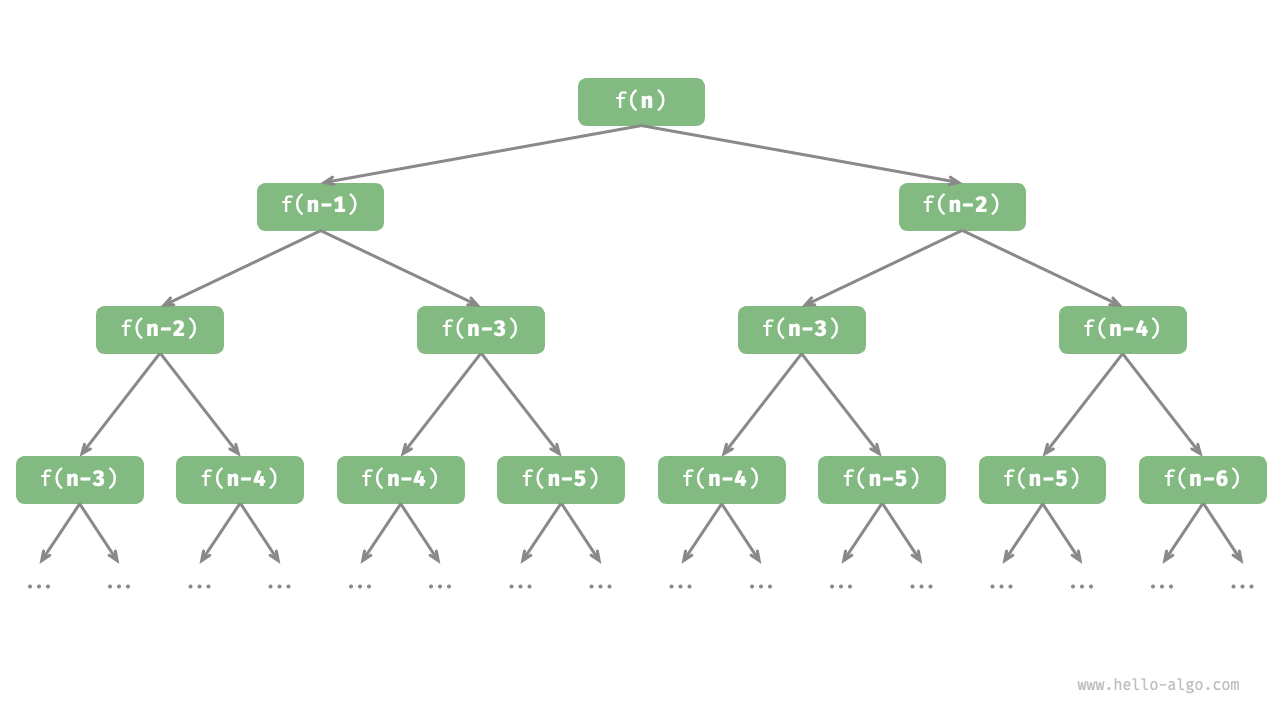
image

// 斐波那契问题：数列前n项和：0 1 1 2 3 5 8
int fibo(int i)
{
    if (i == 1) return 0;
	if (i == 2) return 1;
    return fibo(i-1) + fibo(i-2);
}

时间复杂度

image
image

#include <iostream>

/* 复杂度2^n，例如上一节的fibo */
int Exp1(int n)
{
    int m = 1;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; ++j)
        {
            std::cout << "test" << std::endl;
        }
        //共需执行1+2+4+8+16+32+64+128+...+2^n次方次
        m *= 2;
    }
}

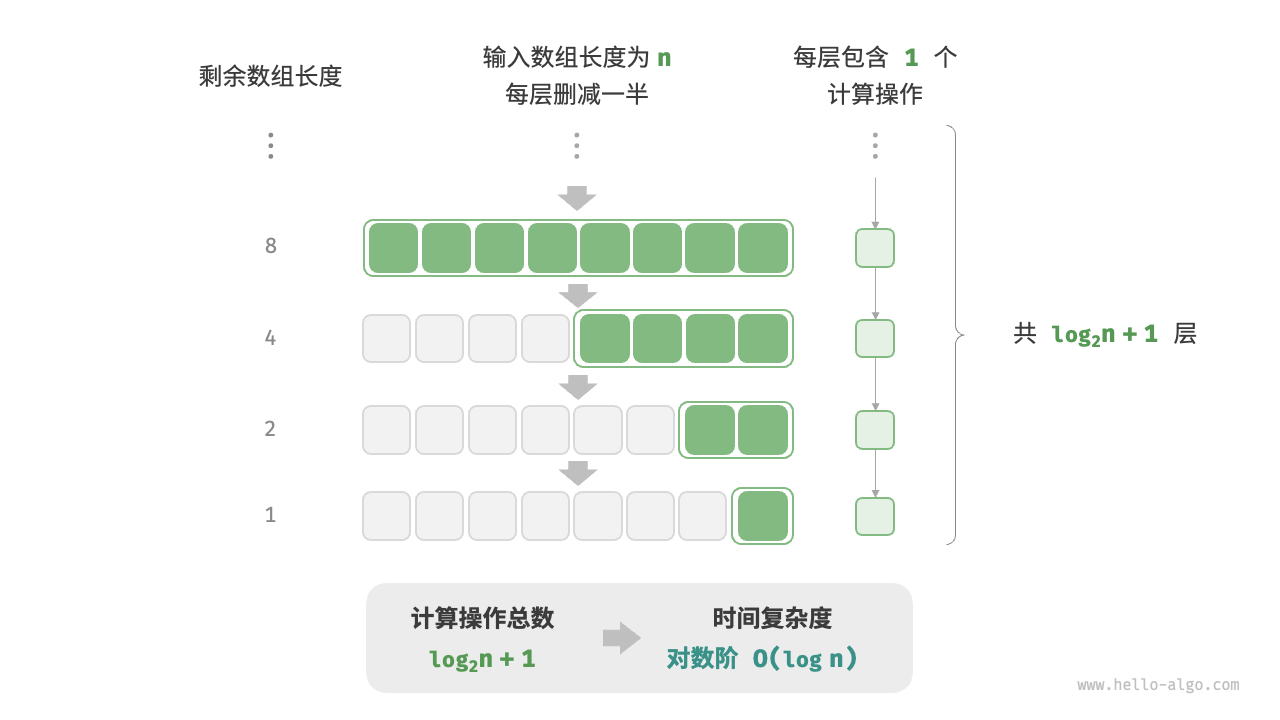
/* 复杂度logn 多出现在分治策略中 */
int Exp2(int n)
{
    //假设n为128，打印依次为:64 32 16 8 4 2 1,即执行次数为7，由于每次除2，故与log2n相关
    while(n != 1)
    {
        n = n / 2;
        std::cout << n << std::endl;
    }
       
}

int Exp3(int n)
{
    if(n <= 1) return 1;
    return Exp3(n/2) + 1;
}

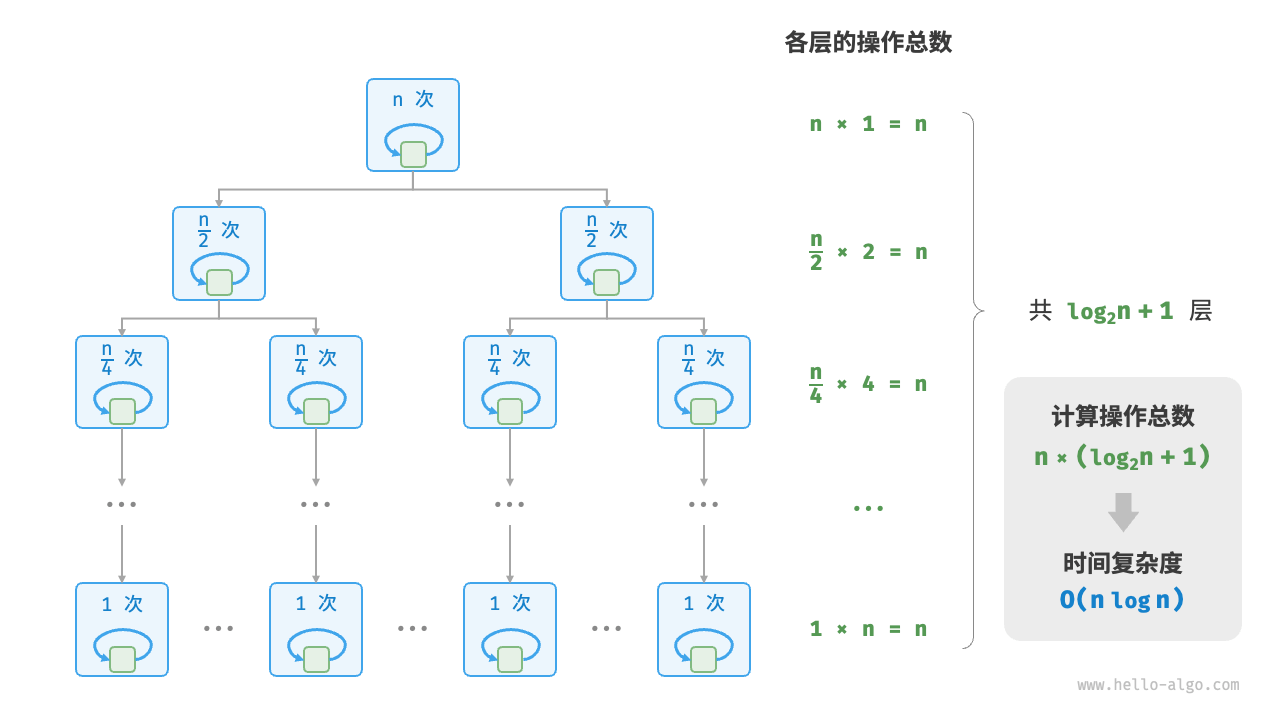
/* 复杂度nlogn 多出现在排序算法中 */
int Exp4(int n)
{
    if(n <= 1) return 1;
    int cnt = Exp4(n/2) + Exp4(n/2);
    for (int i = 0; i < n; i++)
    {
        cnt++;
    }
    //n + n/2 * 2 + n/4 * 4 + ... = nlogn
}

/* 复杂度n!=n*(n-1)*(n-2)*...*1 */
int Exp5(int n)
{
    if (n == 0) return 1;
    int cnt = 0;
    for (int i = 0; i < n; i++)
    {
        cnt += Exp5(n-1);
    }
    //例如Exp(5) 需要执行5次Exp(4),每次Exp(4)需要执行4次Exp(3) 最后总共需要执行5*4*3*2*1
}

空间复杂度

  • 输入空间：存储算法的输入数据
  • 暂存空间：存储算法运行过程中的变量上下文。包含暂存数据(常量 变量 对象) 栈帧空间(上下文 ) 指令空间(编译后的程序指令，忽略不计)
  • 输出空间：存储算法的输出数据
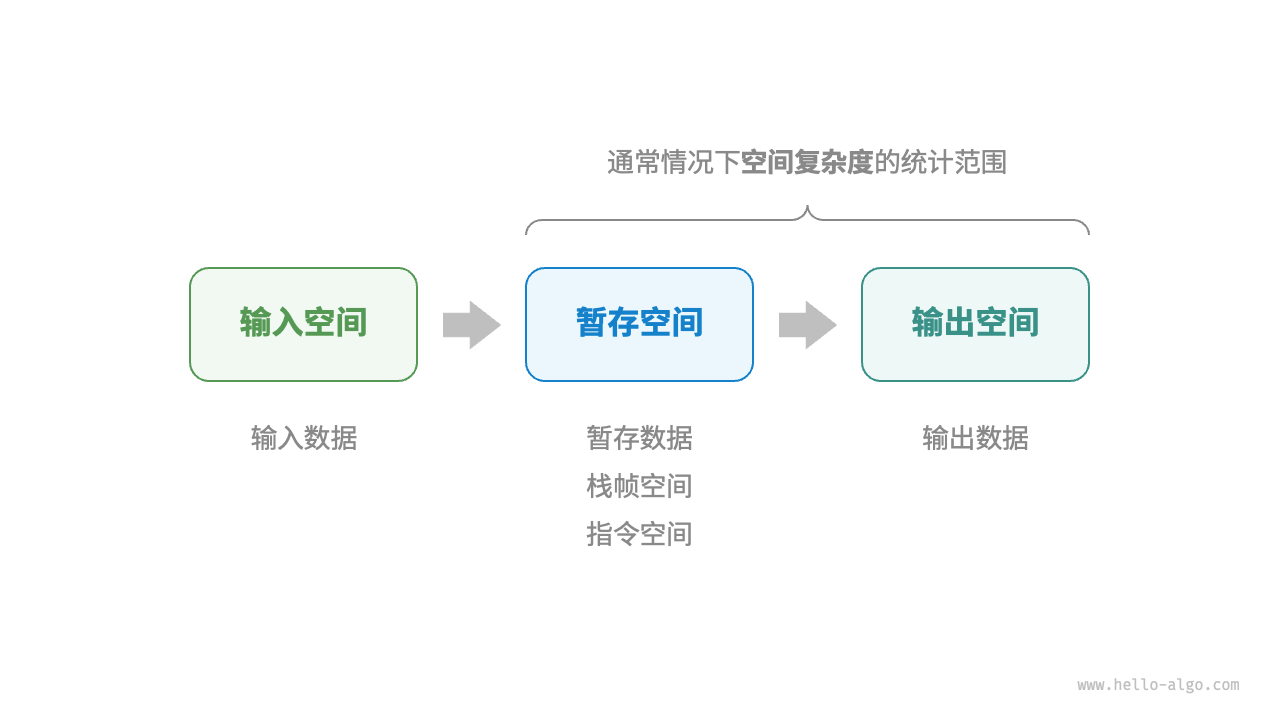
    image

空间复杂度只关注最差，因为内存空间是硬性要求

  • 常见的空间复杂度：
  1. 普通变量 长度固定的数组链表等，空间复杂度O(1)
  2. 长度为n的数组链表，空间复杂度O(n)
  3. 每次循环中的函数调用，空间复杂度O(1)，不用乘循环次数，因为每时刻都只有一个函数未返回
  4. 递归深度n的函数调用，空间复杂度O(n) 因为最多会出现n个递归同时未返回
  5. 满二叉树空间复杂度O(2^n)4
  6. 分治算法，输入长度n的数组，每轮从中间划分为两半，一直递归，形成对数阶空间复杂度

数据结构

分类

  1. 线性：数组 链表 栈 队列 哈希表，元素之间一对一
  2. 非线性：分为树形和网型
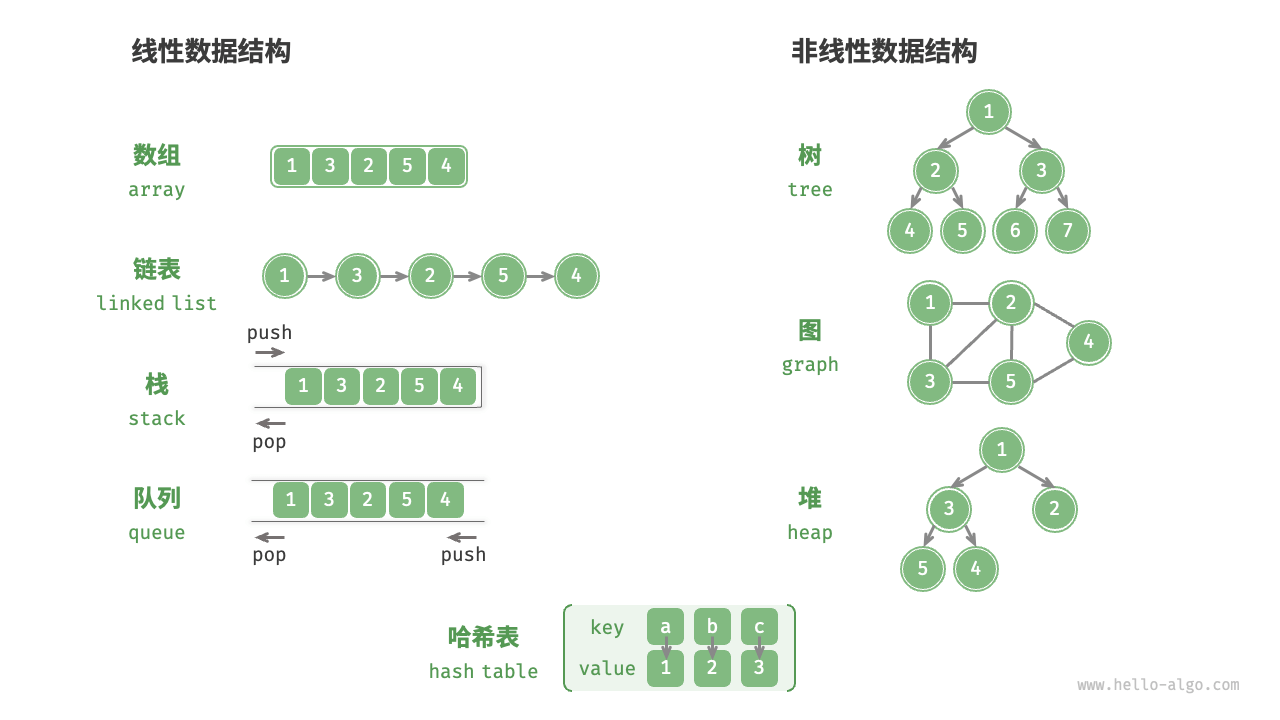
    image
  3. 所有数据结构都是基于数组和链表实现的

数字编码

数字以补码形式存储在计算机中

  1. 原码：数字的二进制形式，最高符号位，0正1负，其余位表示值
  2. 反码：正数反码等于原码，负数反码是除最高符号位，其他取反
  3. 补码：正数补码等于原码，负数的补码等于反码+1

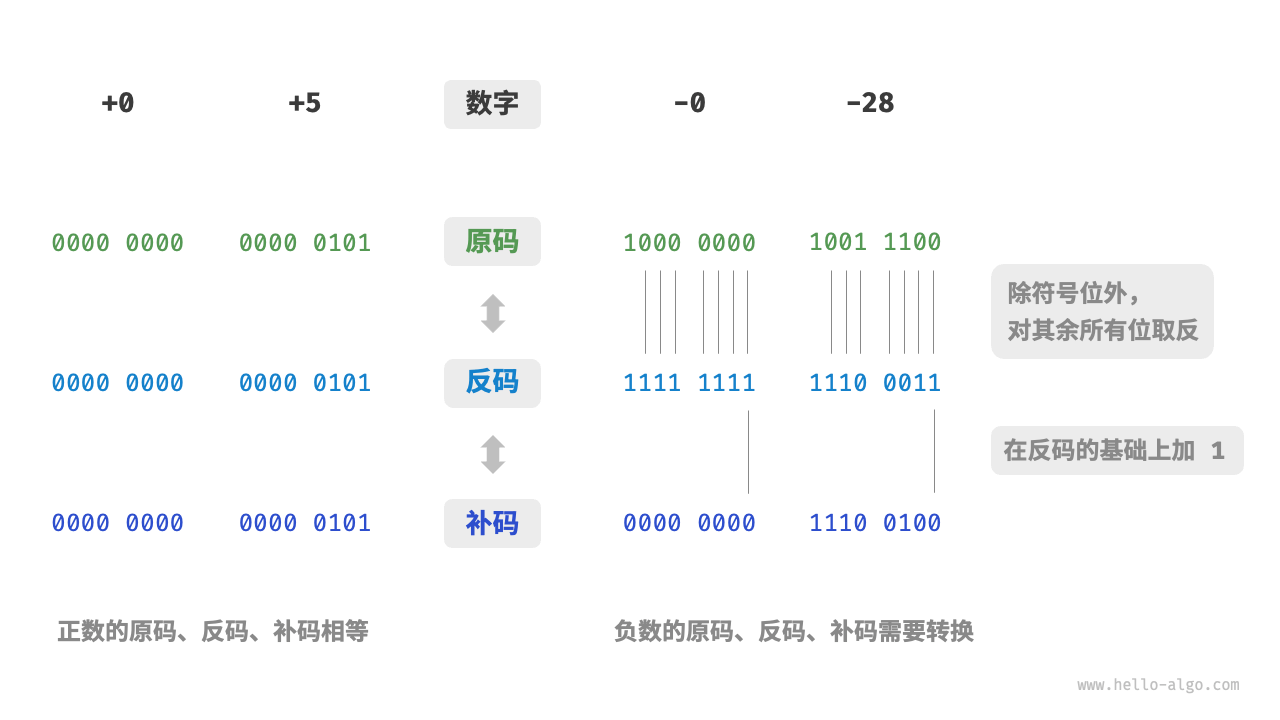
image

  • 这里-0的补码其实是100000000，但是溢出8位了，把最高位舍弃其实就是+0

  • 对于补码：1000 0000 逆推的原码是0000 0000 这个不合理，因为该原码对应的是0（原 补可以一对多） 因此这个特殊的补码被规定为-128，可以通过（-1） + （-127） 得到
    image

  • float double是用符号位、指数位、分数位区分的

字符编码

GB2312--GBK--UniCode--utf-8

数组与链表

数组

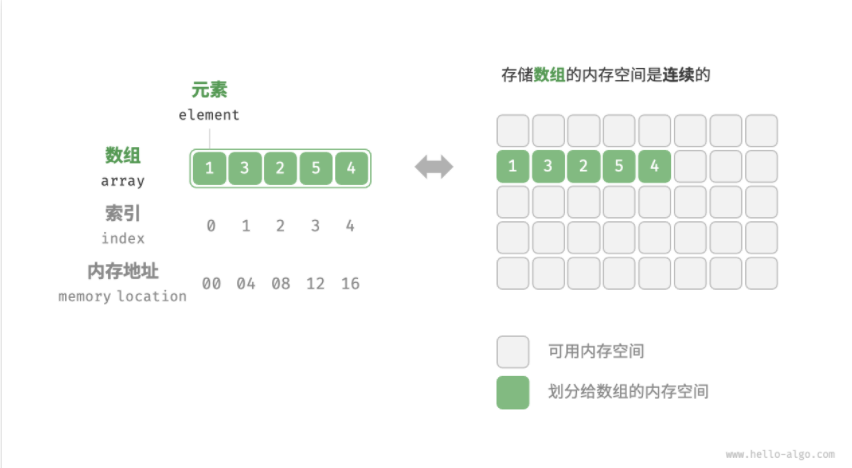
image

  • 优点：空间效率好（连续内存分配） 支持随机O(1)访问数据 缓存局部性(访问数据元素不止加载他，还会缓存他附近的其他元素)
  • 缺点：插入与删除效率低 长度不可变，扩容操作耗费资源 分配长度不合理造成空间浪费

链表

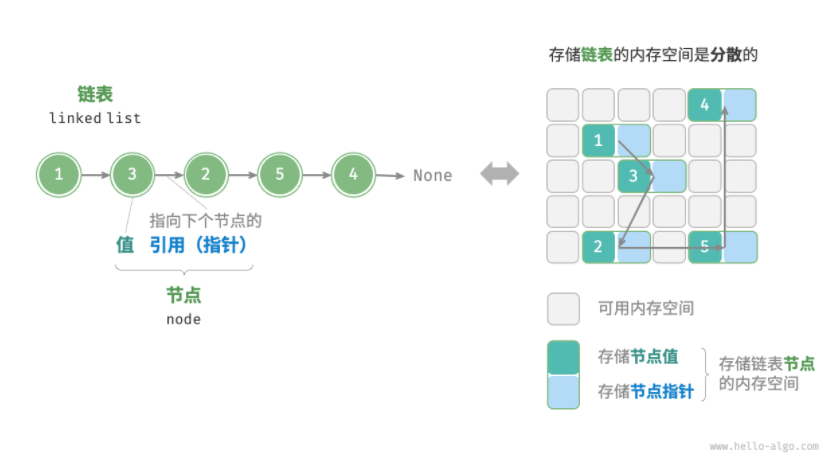
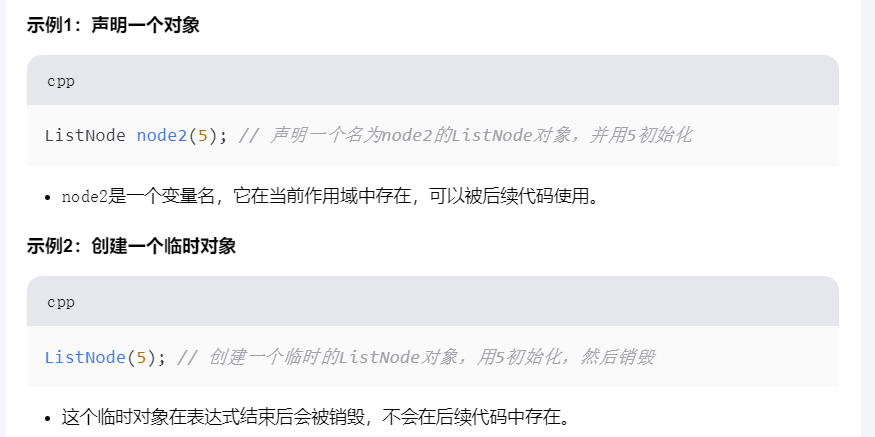
image

image

列表

列表是个抽象概念，表示元素的有序集合，可以基于链表or数组实现

  • c++的vector是基于动态数组实现的列表

image

内存与缓存

  1. 计算机存储设备有三种：硬盘、内存（RAM）、磁盘

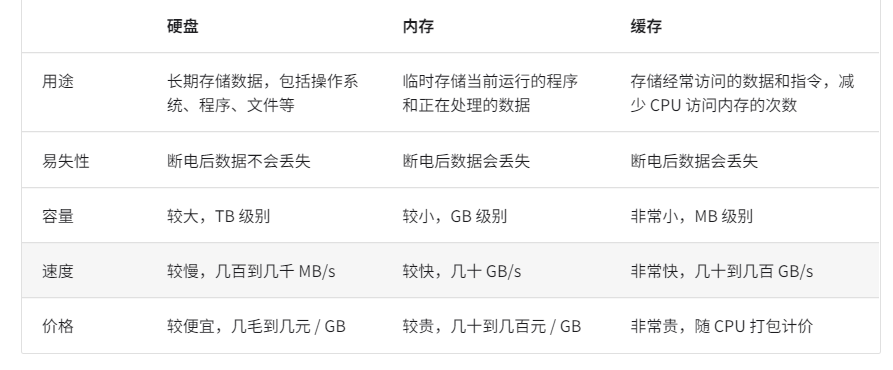
image

  1. CPU尝试访问的数据不在缓存中，那么就要去内存中取，速度变慢，引出缓存命中率概念

  2. 为了提高命中率主要有四种措施：缓存行(一次不止缓存一个字节) 预取(循环时预测到下一个会取xxx，提前拿到) 空间局部性(访问一个元素 同时加载上他附近的) 时间局部性(被访问过一次就有更大几率再次被访问)

  3. 数组比链表缓存命中率更高：同样信息量数组占空间小、可预测性强、按行加载更不可能出现一堆无效数据、数据顺序存储符合空间局部性

栈与队列

栈

  • 先入后出，栈顶入，栈顶出

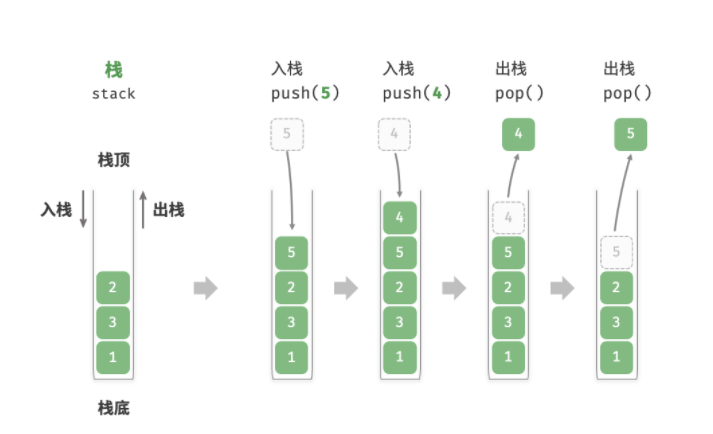
image

  • 基于数组实现的栈总体效率更高，但是如果触发数组扩容操作会导致效率下降
  • 基于链表实现的栈更稳定
  • 浏览器的前进后退，通常都是栈，同时支持前进和后退就是要俩栈

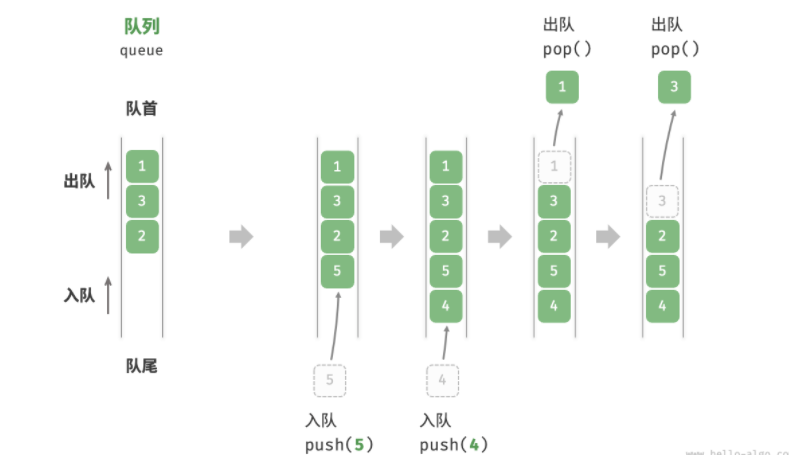
队列

  • 先入先出，队尾入 队首出（其实队首进 队尾出也可以 但是为了模拟排队，都是从前往后排的）

image

posted @ 2025-01-10 00:01  __Zed  阅读(105)  评论(0)    收藏  举报