KMP算法

用于解决字符串匹配问题

解决什么问题

比如要找字符串"123123124"中的"123124"在哪个位置，肉眼一看就知道是最后6个字符，刨根来看，我们从头开始看，看到12312还是匹配的，123123就不匹配了，那这不浪费了刚刚看的那么多么，所以就想了个招，第二个123可以看作第一个123继续匹配，这样就可以跳过从23123 3123...匹配的步骤了
也就是说，这个算法只能化简要找A中的B，这个B必须是有xyz ... xyz 这样结构才可以,至少需要abcedfa！！！！！！！

名词解释

前缀表

1. 前缀：包含首字母不包含尾字母的所有子串

• 比如aabaaf的前缀有a aa aab aaba aabaa

2. 后缀：包含尾字母不包含首字母的所有子串

• 比如aabaaf的后缀有f af aaf baaf abaaf

3. 最长相等前后缀：比如aabaa，最长的，相等的，前缀和后缀相等，那么这个缀就是aa，长度是2

子串	最长相等前后缀长度
a	0
aa	1
aab	0
aaba	1
aabaa	2
aabaaf	0

于是前缀表就是0 1 0 1 2 0

巧妙的地方所在

1. 最长相等前后缀，一定发生在两端(所以最长相等前后缀是几，就从后往前数几个，不会出现跳过某个的情况)！！！因为前缀要求包含首 后缀要求包含尾
2. aabaa还可以匹配上，aabaaf匹配不上了，就找到f前面的最长相等前后缀“aa”,也就是说前面也有个aa，那么继续用这个aa匹配
   
3. 相当于说，不用KMP，如果aabaaf匹配不上了，需要从索引1开始(第二个位置)继续匹配，但这是无效的，因为首是aa，所以KMP帮你跳到最近的有效位置
4. 跳到的这个位置'b'下标是多少呢，刚好是2（最长相等前后缀长度）！！！

题解

求前缀表（也就是next数组）即0 1 0 1 2 0, 都是相对于模式串来说的

1. 定义 i 指向后缀末尾 j 指向前缀末尾， 什么意思呢，比如aaba这个模式串子串，i依次要指向a b a, j依次要指向a a b

2. next[0] = 0;
   

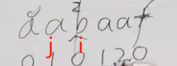
3. 遇见冲突(si≠sj)找前一位，比如上图，现在正在求aaba的前缀表，j就要跳到他的前一位对应的前缀表的值的下标处 也就是0处（巧妙地方所在的第四条）

流程模拟

abab的话，j=0 i=1, 不匹配 next[i] = 0, 继续下次循环i++，a a匹配了，此时next[i]=++j，循环结束i++，next[i]=++j
对于aabaaf

1. 初始化 next[0]=0 j=0指向前缀结尾，i=1指向后缀结尾
2. next[1], s[i]=s[j],next[i]=++j; 然后下一轮循环i++
3. next[2]，不匹配，j前移到第一个位置，仍然不匹配但是无法前移了，所以只好下一轮循环i++
4. next[3]，匹配，next[i]=++j,下一轮循环i++
5. next[4], 匹配，next[i]=++j,下一轮循环i++
6. next[5]，不匹配，j前移到第一个a,仍然不匹配但是无法前移了，所以只好下一轮循环i++，循环结束

通俗易懂的理解

相当于说把模式串看成拉链，往文本串里卡，卡到f的位置卡不上了，此时发现aab"aa"baaf这两个aa和前面的aa重复了，而前面的aa已经和模式串前面的aa匹配过了, 既然都是aa，那么就把模式串卡在文本串后面的aa上，节省了a"aba"abaaf这么长的距离

是怎么找到的aa呢，是通过aaba"a"f的最长相等前后缀是2，找到了b的位置，卡上了b前面的aa

怎么确定这样跳跃不会漏掉呢？“最长”保证！！揭开之后，模式串肯定是从头找的呀，最长就意味着是后缀的最靠前的位置了！！

寻找前缀表时，j到底是怎么前移的？

比如cbcdcbce, 匹配到cbcdcbc，此时j i都指向c，匹配后j++并赋值给next[i] 下一轮循环i++,此时i指向e,j指向d
看作 cbcd cbce，同上，cbcd往cbce上卡，卡到d卡不上了，于是想着找c, cbcd前面有c，
于是现在是 ：

c b c e
    c b c d

此时j指向b，这个b咋来的呢，j = next[j-1] = 1
发现仍然不匹配，那么就继续找b前一个c，前面是否还有与c匹配的了？没有了，也就是next[j-1]=0了，所以j=0，跳到最开头了，
于是现在是：

c b c e
      c b c d

此时j指向c i仍然指向e, 还不相等，跳到最开头了，只好作罢，给next[i]赋值0，表示没有可匹配的