Integer Optimization(借助ortools)

注：中文非直接翻译英文，而是理解加工后的笔记，记录英文仅为学其专业表述。

目录

• Mixed-Integer Programming
  • MIP solvers
  • 对比线性和整数规划
• CP Approach to Integer Optimization
  • eg: 转换非整数约束
    • 用CP-SAT求解器来解
    • 用原始CP求解器来解

Mixed-Integer Programming

变量部分（非全部）为整数的问题，可以用混合整数规划来解决Mixed Integer Programming (MIP)。MIP也可称为混合整数线性规划问题，Mixed Integer Linear Programming (MILP)。

MIP solvers

OR-Tools 提供多种MIP求解器，默认是开源求解器 Coin-or branch and cut (CBC)。如果从源码安装，可以使用其他第三方求解器如:

• SCIP
• GLPK
• Gurobi

步骤:

• 导入求解器
• 声明求解器
• 调用求解器

eg:

• 目标: maximize(x + 10y)
• 约束:
  • x + 7 y ≤ 17.5
  • x ≤ 3.5
  • x ≥ 0
  • y ≥ 0
  • x, y 都是整数

from ortools.linear_solver import pywraplp

def main():
    # Create the mip solver with the CBC backend.
    solver = pywraplp.Solver('simple_mip_program',
                             pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)

    infinity = solver.infinity()
    # x and y are integer non-negative variables.
    x = solver.IntVar(0.0, infinity, 'x')
    y = solver.IntVar(0.0, infinity, 'y')

    print('Number of variables =', solver.NumVariables())

    # x + 7 * y <= 17.5.
    solver.Add(x + 7 * y <= 17.5)

    # x <= 3.5.
    solver.Add(x <= 3.5)

    print('Number of constraints =', solver.NumConstraints())

    # Maximize x + 10 * y.
    solver.Maximize(x + 10 * y)

    result_status = solver.Solve()
    # The problem has an optimal solution.
    assert result_status == pywraplp.Solver.OPTIMAL

    # The solution looks legit (when using solvers others than
    # GLOP_LINEAR_PROGRAMMING, verifying the solution is highly recommended!).
    assert solver.VerifySolution(1e-7, True)

    print('Solution:')
    print('Objective value =', solver.Objective().Value())
    print('x =', x.solution_value())
    print('y =', y.solution_value())

    print('\nAdvanced usage:')
    print('Problem solved in %f milliseconds' % solver.wall_time())
    print('Problem solved in %d iterations' % solver.iterations())
    print('Problem solved in %d branch-and-bound nodes' % solver.nodes())


if __name__ == '__main__':
    main()

运行得

Number of variables = 2
Number of constraints = 2
Solution:
Objective value = 23.0
x = 3.0
y = 2.0

Advanced usage:
Problem solved in 28.000000 milliseconds
Problem solved in 1 iterations
Problem solved in 0 branch-and-bound nodes

• solver.NumVar 实数变量
• solver.IntVar 整数变量

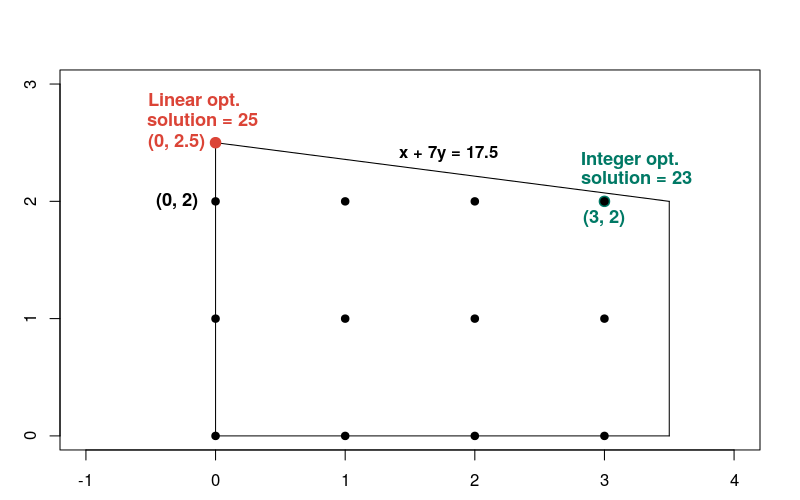
对比线性和整数规划

猜测整数规划的解也许接近线性规划，但情况并非如此。

You might guess that the solution to the integer problem would be the integer point in the feasible region closest to the linear solution — namely, the point x = 0, y = 2. But as you will see next, this is not the case.

替换约束条件为

    infinity = solver.infinity()
    x = solver.NumVar(0, infinity, 'x')
    y = solver.NumVar(0, infinity, 'y')

    print('Number of variables =', solver.NumVariables())

运行得

Number of variables = 2
Number of variables = 2
Number of constraints = 2
Solution:
Objective value = 25.0
x = 0.0
y = 2.5

Advanced usage:
Problem solved in 20.000000 milliseconds
Problem solved in 0 iterations
Problem solved in 0 branch-and-bound nodes

CP Approach to Integer Optimization

约束优化（CP）不同于传统优化理论，它更关注约束和变量，而不是目标函数。有些问题，CP可以比MIP求解器更快地找到最优解。

• 对于标准整数规划问题，可行点必须满足所有约束，MIP求解速度更快。在这种情况下，可行集是凸的：对于集合中的任意两点，连接它们的线段完全位于集合中。

• 对于具有高度非凸可行集的问题，CP-SAT解算器通常比MIP解算器更快。当可行集由多个“或”连接的约束定义时，意味着一个点只需要满足其中一个约束即可。

eg: 转换非整数约束

为了提高计算速度，CP-SAT解算器和原始CP解算器都对整数进行运算。

To solve a problem in which some of the constraints have non-integer terms, you must first transform those constraints by multiplying them by a sufficiently large integer.

eg:

• 目标: maximize(2x + 2y + 3z)
• 约束:

\begin{align} x+\frac{7}{2}y+\frac{3}{2}z\leq25 \\ 3x - 5y + 7z \leq 45 \\ 5x + 2y - 6z \leq 37 \\ x, y, z \geq 0 \\ x, y, z \quad integers \\ \end{align}

用CP-SAT求解器来解

from ortools.sat.python import cp_model

def main():
  model = cp_model.CpModel()
  var_upper_bound = max(50, 45, 37)
  x = model.NewIntVar(0, var_upper_bound, 'x')
  y = model.NewIntVar(0, var_upper_bound, 'y')
  z = model.NewIntVar(0, var_upper_bound, 'z')

  model.Add(2*x + 7*y + 3*z <= 50)
  model.Add(3*x - 5*y + 7*z <= 45)
  model.Add(5*x + 2*y - 6*z <= 37)

  model.Maximize(2*x + 2*y + 3*z)

  solver = cp_model.CpSolver()
  status = solver.Solve(model)

  if status == cp_model.OPTIMAL:
    print('Maximum of objective function: %i' % solver.ObjectiveValue())
    print()
    print('x value: ', solver.Value(x))
    print('y value: ', solver.Value(y))
    print('z value: ', solver.Value(z))

if __name__ == '__main__':
  main()

运行得

Maximum of objective function: 35

x value:  7
y value:  3
z value:  5

用原始CP求解器来解

from ortools.constraint_solver import pywrapcp
from ortools.constraint_solver import solver_parameters_pb2

def main():
  # Instantiate a CP solver.
  parameters = pywrapcp.Solver.DefaultSolverParameters()
  solver = pywrapcp.Solver('simple_CP', parameters)
  var_upper_bound = max(50, 45, 37)
  x = solver.IntVar(0, var_upper_bound, 'x')
  y = solver.IntVar(0, var_upper_bound, 'y')
  z = solver.IntVar(0, var_upper_bound, 'z')
  solver.Add(2*x + 7*y + 3*z <= 50)
  solver.Add(3*x - 5*y + 7*z <= 45)
  solver.Add(5*x + 2*y - 6*z <= 37)
  objective = solver.Maximize(2*x + 2*y + 3*z, 1)
  decision_builder = solver.Phase([x, y, z],
                                  solver.CHOOSE_FIRST_UNBOUND,
                                  solver.ASSIGN_MAX_VALUE)
    # Create a solution collector.
  collector = solver.LastSolutionCollector()
  # Add the decision variables.
  collector.Add(x)
  collector.Add(y)
  collector.Add(z)
  # Add the objective.
  collector.AddObjective(2*x + 2*y +3*z)
  solver.Solve(decision_builder, [objective, collector])
  if collector.SolutionCount() > 0:
    best_solution = collector.SolutionCount() - 1
    print("Maximum of objective function:", collector.ObjectiveValue(best_solution))
    print()
    print('x= ', collector.Value(best_solution, x))
    print('y= ', collector.Value(best_solution, y))
    print('z= ', collector.Value(best_solution, z))

if __name__ == '__main__':
  main()

运行得

Maximum of objective function: 35

x=  7
y=  3
z=  5