【文化课学习笔记】【数学】统计与概率

【数学】统计与概率

统计

定义

为了实现某种调查目的，进行收集数据，整理数据，分析数据。

收集数据

方法：全面调查和抽样调查。

全面调查：调查所有对象。优点：全面。缺点：工作量大。

抽样调查：从全体中抽取一部分样本调查。抽样调查必须保证每个个体有相同的几率被抽到。

高中阶段介绍了三种抽样调查：简单随机抽样、系统抽样和分层抽样。

简单随机抽样

适用范围：当总体中的个体之间差异程度较小，并且总体中个体数目较少时，通常采用这种方法。

内容：抽签，随机数法。

系统抽样（等距抽样）

适用范围：总体数量和需要抽取的数量都比较大。

内容：先分段在第一段中随机抽取一个，再依次加上分段间隔。

例如：在 \(1000\) 名学生中抽取 \(100\) 人，根据系统抽样，可以首先将 \(1000\) 个人平均分为 \(100\) 段，每段 \(10\) 人，将每一段的所有人从 \(1\) 到 \(10\) 编号，然后在 \(1\) 到 \(10\) 中随机抽取一个编号，对每一段都抽取这个编号。则抽到的 \(100\) 个人即为所求。

分层抽样（按比例抽样）

适用范围：调查对象可分成有明显差别的、互不重叠的几部分。

内容：每一部分可称为层，在各层中按层在总体中所占比例进行随机抽样。

例如：某校有 \(300\) 名男生，\(700\) 名女生，需要抽取 \(100\) 人调查身高情况。

由于身高与性别有关，所以需要分层。可以按照男女比例为 \(3:7\) 抽取 \(30\) 个男生，\(70\) 个女生，调查身高。

整理数据

茎叶图

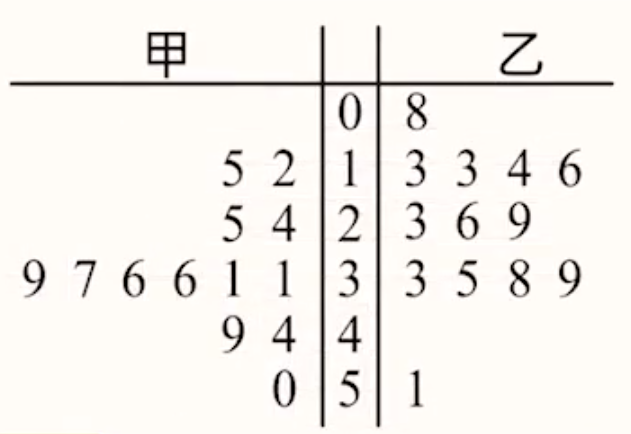
以上图为例。中间一列叫做茎，表示高位数字，甲和乙共用。两边的列叫做叶，表示低位数字，甲和乙各自用。

观察时可一行一行看，那么甲对应的数为 \(0,12,15,24,25,\cdots\)，乙对应的数为 \(8,13,13,14,16,23,26,29,\cdots\)。

频率分布直方图

频数：对应区间有几个对象（出现的次数）。

频率：对应区间占总人数的比（比值）。所有的频率之和为 \(1\)。

频数分布直方图的纵坐标表示频数，即每个组的个数；频率分布直方图纵坐标不表示频率，而表示 \(\dfrac{频率}{组距}\)，组距即为每一组对应区间的端点之差。

做有关频率分布直方图的问题时，应该先找到组距，再根据组距 \(\times\) 纵坐标求得每一组的频率。

在频率分布直方图中，每个矩形的面积即为频率。

技巧方法：

• 利用频率分布直方图估计平均数时，可以通过直方图求出每组的频率，然后通过每组频率 \(\times\) 对应组的组中值 再相加的方式估算。注意：若题目告诉用每组的某个对应值代替每组的平均数，则直接代入即可；若没有告诉，则利用对应组的组中值代替平均数。
• 利用频率分布直方图比较两个平均数的大小时，不一定非要计算出每一组的平均数然后再比较大小，有时候作差法更简便，只需要判断 \(\overline{x_1} - \overline {x_2}\) 和 \(0\) 的大小关系即可。
• 利用频率分布直方图估计中位数时，由于每一组的矩形面积即为每一组的频率，则需要找到一条直线 \(x = a\) 平分图中所有矩形面积，通过图形找出对应 \(x = a\) 所在组然后根据面积估算即可。
• 利用频率分布直方图比较两个方差的大小时，若非解答题，一般情况下可以不用计算出每组数的方差，只需要观察两组的频率分布直方图，找出两组数离散程度（分布的均匀程度）比较即可。往往数据分布较为集中的方差较小。

分析数据

统计量

表示数据集中程度：平均数，中位数，众数。

表示数据离散程度：极差，方差，标准差。

平均数

定义：给定一组数 \(x_1,x_2, \cdots,x_n\)，则其平均数为 \(\overline x = \dfrac 1 n (x_1 + x_2 +\cdots + x_n)\)，常记为 \(\overline x = \dfrac 1 n \sum \limits_{i = 1}^n x_i\)。

用频率计算平均数：将每个数与其出现的频率相乘，再相加。

性质：

• 把一组数同时加上 \(b\)，则平均数也加 \(b\)。
• 把一组数同时乘上 \(a\)，则平均数也乘 \(a\)。

中位数

定义：

• 如果一组数有奇数个，且按照从小到大排列 \(x_1,x_2,\cdots,x_{2n + 1}\)，则 \(x_{n+1}\) 为中位数。
• 如果一组数有偶数个，且按照从小到大排列 \(x_1,x_2,\cdots,x_{2n}\)，则 \(\dfrac{x_n + x_{n + 1}}{2}\) 为中位数。

性质：

• 把一组数同时加上 \(b\)，则中位数也加 \(b\)。
• 把一组数同时乘上 \(a\)，则中位数也乘 \(a\)。

众数

定义：一组数据中，出现次数最多的数据。众数可以不唯一。

如果所有数出现的次数相同，则没有众数。

性质：

• 把一组数同时加上 \(b\)，则众数也加 \(b\)。
• 把一组数同时乘上 \(a\)，则众数也乘 \(a\)。

极差

定义：一组数的极差指的是这组数的最大值减去最小值的差。

性质：

• 把一组数同时加上常数 \(b\)，则极差不变。
• 把一组数同时乘上常数 \(a\)，则极差乘 \(|a|\)。

方差和标准差

定义：如果 \(x_1,x_2,\cdots,x_n\) 的平均数为 \(\overline x\)，则方差 \(s^2 = \dfrac 1 n \sum \limits_{i = 1}^n (x_i - \overline x)^2\)。其中方差的算术平方根 \(s\) 称为标准差。

本质：方差表示的是一组数偏离平均数的偏离程度。

求方差的步骤：

1. 求平均数。
2. 每个数减去平均数再平方。
3. 求第二步得到的所有数的平均数。

用频率计算方差：用每个数减去平均数，然后乘上频率再相加，即 \(s^2 = \sum \limits_{i = 1}^{n} (x_i - \overline x)^2\cdot p_i\)。

方差的性质：

• 把一组数同时加上常数 \(b\)，则方差不变。
• 把一组数同时乘上常数 \(a\)，则方差乘 \(a^2\)。

标准差的性质：

• 把一组数同时加上常数 \(b\)，则标准差不变。
• 把一组数同时乘上常数 \(a\)，则标准差乘 \(|a|\)。

性质规律总结

把一组数同时加上常数 \(b\)，则：平均数、中位数、众数都 \(+b\)，极差、标准差、方差都不变。

把一组数同时乘上常数 \(a\)，则：平均数、中位数、众数都 \(\times a\)，极差、标准差都 \(\times |a|\)，方差 \(\times a^2\)。

小技巧：求两组数平均数的差，除了可以将两者平均数分别算出再作差之外。当两组数个数相同时，还可以对两组数对应位置的数相减，再将得到的值相加，除以个数。

计算&书写技巧

1. 计算平均数时，对于数据较多，但数据均分布在某个特定值 \(x\) 附近的样本，可以考虑先求出每个数 \(x_i\) 和 \(x\) 的差，然后对它们的差求平均数再加上 \(x\)。即 \(\overline x = \dfrac 1 n \sum \limits_{i = 1}^n (x_i - x) +x\)，且一般情况下多个 \(s = (x_i - x)\) 相加，很多 \(|s|\) 相同，可以直接正负抵消。
2. 计算方差 \(s^2\) 时，书写过程时可以省略 \((x_i - \overline x)\)，即直接把 \((x_i - \overline x)\) 的结果写在考卷上，且一般情况下 \((x_i - \overline x)\) 比较容易口算。

例题

例 1：\(4\) 名同学各掷了 \(5\) 次骰子，分别记录每次骰子出现的点数。若下列是根据 \(4\) 名同学各自的统计结果的数字特征，则可以判断出一定没有点数 \(6\) 的是（）

A. 平均数为 \(3\)，中位数为 \(2\)

B. 中位数为 \(3\)，众数为 \(2\)

C. 中位数为 \(3\)，方差为 \(2.8\)

D. 平均数为 \(2\)，方差为 \(2.4\)

---

分析：

对于选项 A，设五个数中其它三个数为 \(a,b,c\)，其中 \(a,b \le 2\)，\(2 \le c \le 6\)，则有 \(a + b + 2 + c + 6 = 3 \times 5 = 15\)，所以 \(a + b + c = 7\)，令 \(a = 2,b = 2,c = 3\) 满足条件。

对于选项 B，假设出现了两次 \(2\)，则可以构造 \(2,2,3,4,6\) 满足条件。

对于选项 C，设其它三个数为 \(a,b,c\)，则有 \((a - x)^2 + (b - x)^2 + (3 - x)^2 + (c - x)^2 + (6 - x)^2 = 2.8 \times 5 = 14\)，且 \(a + b + 3 + c + 6 = 5x\) 即 \((a - x) + (b - x) + (3 - x) + (c - x) + (6 - x) = 0\)，令 \(a = 1,b = 2,c = 3\) 满足条件。

对于选项 D，设其它四个数为 \(a,b,c,d\)，则从平均数的角度来说，有 \(a + b + c + d + 6 = 10\)，此时 \(a = b = c = d = 1\)，此时方差 \(s^2 \ne 2.4\)，故 D 一定没有点数 \(6\)；从方差的角度来说，有 \((a - 2)^2 + (b - 2)^x + (c - 2)^2 + (d - 2)^2 + (6 - 2)^2 = 2.4 \times 5 = 12\)，由于 \(4^2 = 16 > 12\)，所以一定没有点数 \(6\)。

故选 D。

经验：一般此类题，错误选/项都是涉及到平均数和方差的那个选项，所以考试的时候可以考虑先验证该选项。

---

例 2：如图所示， 在 \(50\) 名样本中，从其成绩在 \(80\) 分及以上的学生中随机抽取 \(3\) 人，用 \(X\) 表示其成绩在 \([90,100]\) 中的人数，用 \(Y\) 表示其成绩在 \([80,90)\) 的人数，试判断方差 \(D(X)\) 和 \(D(Y)\) 的大小关系。

分析：

由题意可得 \(X + Y = 3\)，所以 \(Y = -X + 3\)，所以根据方差的性质可知，\(D(Y) = (-1)^2 D(X) = D(X)\)，所以 \(D(Y) = D(X)\)。

注意：大部分比较方差的题目，不需要将具体的方差求出来，可以通过「方差的定义」或「方差的性质」比较大小关系。

性质：若 \(Y = aX + b\)，则 \(D(Y) = a^2 D(X)\)。

概率

定义

事件发生可能性的大小。这里的事件指的是随机事件。

随机试验：结果随机 / 不确定的试验。

样本点与样本空间：我们把随机试验中每一种可能出现的结果，都称为样本点；把由所有样本点组成的集合称为样本空间，通常用大写希腊字母 \(\Omega\) 表示。

随机事件：如果随机试验的样本空间为 \(\Omega\)，则随机事件 \(A\) 是 \(\Omega\) 的一个子集。而且若试验的结果是 \(A\) 中的元素，则称 \(A\) 发生（或出现等），否则，称 \(A\) 不发生（或不出现等）。

事件中的三个概念

【互斥事件】

给定事件 \(A,B\)，若事件 \(A\) 与 \(B\) 不能同时发生，则称 \(A\) 与 \(B\) 互斥。所以互斥事件两个事件的交集为空。

一般地，如果 \(A_1,A_2,\cdots,A_n\) 是两两互斥的事件，则 \(P(A_1 + A_2 + \cdots + A_n) = P(A_1) + P(A_2) + \cdots + P(A_n)\)，即 \(n\) 个事件至少发生一个的概率等于每一个事件各自发生的概率之和。

【对立事件】

给定事件 \(A,B\)，若事件 \(A\) 与 \(B\) 不能同时发生，且 \(A\) 与 \(B\) 必有一个会发生，则称 \(A\) 与 \(B\) 对立，\(A\) 的对立事件记作 \(\overline A\)。所以对立事件中的两个事件互为补集。

所以对立事件一定是互斥事件，即对立事件是互斥事件的充分不必要条件，\(A\) 与 \(B\) 对立 \(\implies A\) 与 \(B\) 互斥。

对于一个事件 \(A\)，有 \(P(A) + P(\overline A) = 1\)。

【相互独立事件】

若事件 \(A\) 是否发生对事件 \(B\) 的发生概率无影响，则称事件 \(A,B\) 相互独立。当 \(P(AB) = P(A)P(B)\) 时，就称事件 \(A\) 与 \(B\) 相互独立（简称独立），即 \(A\) 与 \(B\) 相互独立 \(\iff P(AB) = P(A)P(B)\)，其中 \(P(AB)\) 表示事件 \(A,B\) 同时发生的概率。

计算每个事件发生的概率可以通过目标事件数除以总事件数，总事件数可以利用表格列举法求解。

计算概率的方法

【用频率估计概率】

一般地，如果在 \(n\) 次重复进行的试验中，事件 \(A\) 发生的概率为 \(\dfrac m n\)，则当 \(n\) 很大时，可以认为事件 \(A\) 发生的概率 \(P(A)\) 的估计值为 \(\dfrac m n\)。

【用事件数计算概率（古典概型）】

古典概型：当结果有有限多个，且每种结果出现的可能性相等时即可用此方法。一般情况下题目会给定一个事件，问满足某些条件的概率是多少。

适用范围：题目当中没有给定任何已知的概率。

\[P = \dfrac{目标事件数}{总事件数} \]

辨析——抽取类问题不同类型：

【类型一：有放回抽取】

一般有「古典概型」和「独立事件」两种方法。大部分情况采用「古典概型」，少部分情况采用「条件概率」。

例：一个袋子中有 \(3\) 个红球，\(2\) 个白球，除颜色外均相同，从中有放回抽取 \(2\) 个球，则抽到一红一白的概率是多少。

求解：这里采用古典概型。

\[P = \dfrac{3 \times 2 + 2 \times 3}{5 \times 5} = \dfrac{12}{25} \]

即总事件数：两次抽取，每次都是从 \(5\) 个球中等概率抽取，所以总事件数为 \(5\times 5\)；目标事件数：两种情况，先红后白，先白后红，两种情况的事件数分别相加即可。

【类型二：不放回抽取】

例：一个袋子中有 \(3\) 个红球，\(2\) 个白球，除颜色外均相同，从中无放回抽取 \(2\) 个球，则抽到一红一白的概率是多少。

求解：同样用目标事件数除以总事件数，此时目标事件数不变，总事件数变成「先从 \(5\) 个里面抽 \(1\) 个，再从剩下 \(4\) 个里面抽 \(1\) 个」，如下：

\[P = \dfrac{3 \times 2 + 2 \times 3}{5 \times 4} = \dfrac 3 5 \]

注意：若将题目中「抽到一红一白的概率」改为「抽到两个红球的概率」，则有放回抽取和不放回抽取的目标事件数不同，此时 ，有放回抽取的概率为 \(3 \times 3\)，无放回抽取的概率是 \(3\times 2\)。

【类型三：一次性抽取】

一般情况下用组合数进行计算。

例：一个袋子中有 \(3\) 个红球，\(2\) 个白球，除颜色外均相同，从中一次性抽取 \(2\) 个球，则抽到一红一白的概率是多少。

求解：总事件数是从 \(5\) 个球里面抽 \(2\) 个，即 \(\mathrm C_5^2\)，目标事件数是从 \(3\) 个红球里面抽 \(1\) 个，从 \(2\) 个白球里面抽 \(1\) 个，即 \(\mathrm C_3 ^1 \times \mathrm C_2^1\)，所以有：

\[P = \dfrac{\mathrm C_3^1\cdot \mathrm C_2^1}{\mathrm C_5^2} = \dfrac 3 5 \]

注：若题目没有明确说明抽取方式，只说从几个球里面抽几个，一般情况默认是「一次性抽取」。

观察上述例题发现，「不放回抽取」和「一次性抽取」计算所得的概率相同，实际上多次抽取中「不放回抽取」\(\iff\)「一次性抽取」。

但是有些情况只有在「不放回抽取」中存在，例如题目求「不放回抽取第二次抽到红球的概率」，此时只能按照一次性抽取算。

【用概率计算概率（独立事件）】

适用范围：①已知条件中会告诉某些概率；②某些事件相互独立（互不影响）。

内容：若 \(A,B\) 独立，则 \(P(AB) = P(A)P(B)\)。

注意：利用独立事件求概率一定要拆解拆解成多个事件，再把每种事件的结果相乘求解。例如：求甲、乙两球至少有一个落入盒子的概率，则甲乙两球都有落入和不落入两种情况，原题可以拆解成甲落，乙落；甲落乙不落；甲不落乙落。三种情况各自分别用乘法计算，然后将三种情况下的概率相加即可。也可以反面计算，即用 \(1\)​ 减去两者均不落入盒子的概率。

概率与数列结合

题目特征：一般情况下若题目出现第 \(n\) 的概率用 \(P_n\) 表示，出现下标，则一般说明这是一个概率与数列结合的问题。

解决思路：

先找递推公式，即 \(P_{n-1}\) 和 \(P_n\) 的关系。具体来说，需要找到第 \(n-1\) 次和第 \(n\) 次各自的状态和概率。

• 状态：一般情况下，第 \(n\) 次通常只需要找到目标状态即可，而第 \(n - 1\) 次需要找到所有可以到达第 \(n\) 次目标状态的状态（一般就是所有的可能状态）。
• 概率：一般需要求出所有上述找到的状态的概率，将所有概率都利用 \(P_{n-1}\) 和 \(P_n\) 表示，再找到第 \(n-1\) 次的每个状态到第 \(n\) 次目标状态的概率，从而求出递推公式。

剩下的就是基本的数列问题了，利用数列相关内容求解即可。

例题

例 1：校足球队中的甲、乙、丙、丁四名球员进行传球训练，第 \(1\) 次由甲将球传出，每次传球时，传球者都等可能的将球传给另外三个人中的任何一人，如此不停地传下去，且假定每次传球都能被接到。记开始传球的人为第 \(1\) 次触球者，第 \(n\) 次触球者是甲的概率记为 \(P_n\)，即 \(P_1 = 1\)。证明：数列 \(\left\{P_n - \dfrac 1 4 \right\}\) 为等比数列，并判断第 \(19\) 次与第 \(20\) 次触球者是甲的概率大小。

求解：

首先考虑找出 \(P_n\) 的递推公式。那么首先考虑找到第 \(n\) 次和第 \(n-1\) 次的状态。

与题目有关的状态为：第 \(n\) 次触球者是甲的情况，第 \(n-1\) 次触球者分别是甲乙丙丁的情况。

那么第 \(n\) 次触球者是甲的概率应为 \(P_n\)，第 \(n-1\) 次触球者是甲的概率应该是 \(P_{n-1}\)，所以第 \(n-1\) 次触球者是乙丙丁的概率之和为 \(1- P_{n-1}\)。

考虑从 \(n-1\) 的状态推到 \(n\) 的目标状态，即从 \(P_{n-1}\) 推到 \(P_n\)，那么容易得到 \(P_n = \dfrac 1 3 (1 - P_{n-1}) = - \dfrac 1 3P_{n-1} + \dfrac 1 3\)。

求出递推公式，问题转化为数列问题。

那么首先考虑求出数列 \(\left\{P_n - \dfrac 1 4\right\}\) 的递推公式：

\[\begin{aligned} & P_n = - \dfrac 1 3 P_{n-1} + \dfrac 1 3\\ \implies & P_n - \dfrac 1 4 = - \dfrac 1 3 P_{n-1} + \dfrac 1 {12} \\ \implies & P_n - \dfrac 1 4 = - \dfrac 1 3 \left(P_{n-1} - \dfrac 1 4\right)\\ \end{aligned} \]

因为 \(P_1 - \dfrac 1 4 = \dfrac 3 4 \ne 0\)，所以数列 \(\left\{P_n - \dfrac 1 4\right\}\) 是等比数列。那么 \(P_n\) 的通项公式为

\[P_n - \dfrac 1 4 = \dfrac 3 4 \cdot \left(- \dfrac 1 3\right)^{n-1} \implies P_n = \dfrac 1 4 + \dfrac 3 4 \cdot \left(- \dfrac 1 3\right)^{n-1} \]

那么

\[P_{19} = \dfrac 1 4 + \dfrac 3 4 \cdot \dfrac{1}{3^{18}} > \dfrac 1 4\\ P_{20} = \dfrac 1 4 - \dfrac 3 4 \cdot \dfrac{1}{3^{19}} < \dfrac 1 4 \]

所以 \(P_{19} > P_{20}\)。

---

例 2（多选）：已知数列 \(\{a_n\}\) 的前 \(n\) 项和为 \(S_n\)，且 \(a_i = 1\) 或 \(a_i = 2\) 的概率均为 \(\dfrac 1 2(i = 1,2,3,\cdots,n)\)。设 \(S_n\) 能被 \(3\) 整除的概率为 \(P_n\)，则（）

A. \(P_2 = 1\)

B. \(P_3 = \dfrac 1 4\)

C. \(P_{11} = \dfrac{341}{1024}\)

D. 当 \(n \ge 5\) 时，\(P_n < \dfrac 1 3\)

求解：

A 选项：\(P_2\) 表示 \(S_2\) 能被 \(3\) 整除的概率，即 \(a_1 + a_2\) 被整除的概率。由于 \(a_1 = 1\) 或 \(a_i = 2\) 的概率均为 \(\dfrac 1 2\)，所以 \(a_1\) 和 \(a_2\) 的取值总共有四种情况，\(1+1 = 2\)，\(1+2 = 3\)，\(2+1 = 3\)，\(2 + 2 = 4\)，\(P_2 = \dfrac 1 2\)。A 错误。

B 选项：\(P_3\) 表示 \(S_3\) 能被 \(3\) 整除的概率，即 \(a_1 + a_2 + a_3\) 被整除的概率。考虑 \(a_1,a_2,a_3\) 的每种取值，总共有 \(2\times 2 \times 2 = 8\) 种情况，列举之后发现有 \(2\) 种情况能被 \(3\) 整除，所以 \(P_3 = \dfrac 1 4\)。

CD 选项：

这两个选项都求的是 \(n\) 稍微较大时的情况，所以考虑求出 \(P_n\) 的通项公式。

首先考虑求出 \(P_n\) 的递推公式。由于 \(P_n\) 表示的是「\(S_n\) 能被 \(3\) 整除的概率」，所以考虑从 \(S_n\) 入手解决问题。

求 \(S_n\) 被 \(3\) 整除的情况，可以转化成求 \(S_n\) 除以 \(3\) 的余数情况，即将「整除问题」转化为「余数问题」。那么当 \(S_n\) 除以 \(3\) 的余数为 \(0\) 时，能被 \(3\) 整除，即 \(S_n\) 除以 \(3\) 余数为 \(0\) 的概率就是 \(P_n\)。

那么 \(S_{n-1}\) 除以 \(3\) 余数为 \(0\) 的概率就是 \(P_{n-1}\)，所以 \(S_{n-1}\) 除以 \(3\) 余数不为 \(0\)（余数为 \(1\) 或 \(2\)）的概率为 \(1 - P_{n-1}\)。

然后考虑从 \(P_{n-1}\) 推到 \(P_n\)，只有两种情况：

• \(S_{n-1}\) 除以 \(3\) 余数为 \(1\)，\(a_i = 2\)，此时有 \(\dfrac 1 2\) 的概率会使得 \(S_n\) 除以 \(3\) 的余数为 \(0\)。
• \(S_{n-1}\) 除以 \(3\) 余数为 \(2\)，\(a_i = 1\)，此时有 \(\dfrac 1 2\) 的概率会使得 \(S_n\) 除以 \(3\) 的余数为 \(0\)。

综上：

\[P_n = 0 \cdot P_{n-1} + \dfrac 1 2 (1-P_{n-1}) = - \dfrac 1 2 P_{n-1} + \dfrac 1 2 \]

已知递推公式，求通项公式，观察形式，考虑不动点法。

此时设 \(x = - \dfrac 1 2 x + \dfrac 1 2\)，解得 \(x = \dfrac 1 3\)。考虑给上述公式两边同时减去 \(\dfrac 1 3\)，有：

\[P_n - \dfrac 1 3 = - \dfrac 1 2 P_{n-1} + \dfrac 1 6 = - \dfrac 1 2 \left(P_{n-1} - \dfrac 1 3\right) \]

又因为 \(P_1 - \dfrac 1 3 = - \dfrac 1 3 \ne 0\)，所以 \(\left\{P_n - \dfrac 1 3\right\}\) 时等比数列，公比 \(q = - \dfrac 1 2\)。

所以

\[P_n- \dfrac 1 3 = - \dfrac 1 3 \cdot \left(- \dfrac 1 2\right)^{n-1} \]

那么

\[P_n = \dfrac 1 3 - \dfrac 1 3 \cdot \left(- \dfrac 12\right)^{n-1} \]

代入 \(n = 11\) 得到 C 正确。

由通项公式可知，当 \(n\) 为偶数时，\(P_n > \dfrac 1 3\)，所以 D 错误。

总结：遇到「整除问题」要考虑将其转化成「余数问题」求解。

解题&计算技巧

对于有些事件数较少用事件数计算概率的问题，有时候可以采用「表格法」将所有情况列出，解题时找到对应符合要求的情况计算概率再相加求解。

例题

例：在一个口袋中装有编号分别为 \(1,1,2,3,4,5\) 的六张卡片，这些卡片除编号不同外其它都相同，从口袋中一次性抽 \(3\) 张卡片。求抽出的 \(3\) 长卡片编号之和为奇数的概率。

分析：

一次性抽取问题，考虑通过事件数来计算概率，使用组合数。

那么总事件数为六张卡片中选取三张，即 \(\mathrm C_6^3 = 20\)。由于六张卡片中有 \(4\) 张奇数，\(2\) 张偶数，所以要使得抽到的 \(3\) 张卡片编号之和为奇数，那么只有 \(3\) 奇 \(0\) 偶和 \(1\) 奇 \(2\) 偶两种情况，所以目标事件数为 \(\mathrm C_4^3 \cdot \mathrm C_2^0 + \mathrm C_4^1 \cdot \mathrm C_2^2 = 8\)，所以概率为 \(P = \dfrac 8 {20} = \dfrac 2 5\)。

随机变量

定义

如果随机试验的样本空间为 \(\Omega\)，且对于 \(\Omega\) 中的每一个样本点，变量 \(X\) 都对应有唯一确定的实数值，就称 \(X\) 为一个随机变量。

随机变量一般用大写英文字母 \(X,Y,Z,\cdots\) 或小写希腊字母 \(\xi,\eta,\cdots\) 表示。

随机变量所有可能的取值组成的集合，称为这个随机变量的取值范围。

例如，把扔骰子可能的结果记为 \(X\)，则 \(X\) 可能为 \(1,2,3,4,5,6\)，这里的 \(X\) 即为一个随机变量。

分布列

\(X\)	\(x_1\)	\(x_2\)	\(\cdots\)	\(x_k\)	\(\cdots\)	\(x_n\)
\(P\)	\(p_1\)	\(p_2\)	\(\cdots\)	\(p_k\)	\(\cdots\)	\(p_n\)

第一行表示随机变量 \(X\) 的所有取值，第二行表示每个取值对应的概率。

离散型随机变量的分布列必须满足：

• \(p_k \ge 0,k = 1,2,\cdots,n\)。
• \(\sum \limits_{k = 1}^n p_k = p_1 + p_2 + \cdots + p_n = 1\)。

期望（均值）

\(X\)	\(x_1\)	\(x_2\)	\(\cdots\)	\(x_k\)	\(\cdots\)	\(x_n\)
\(P\)	\(p_1\)	\(p_2\)	\(\cdots\)	\(p_k\)	\(\cdots\)	\(p_n\)

对于上述分布列，则期望 \(E(X) = \sum \limits_{i = 1}^n x_i p_i = x_1p_1 + x_2p_2 + \cdots + x_np_n\)。

性质：若 \(X\) 与 \(Y\) 都是随机变量，且 \(Y = aX + b(a \ne 0)\)，则 \(E(Y) = aE(x) + b,D(Y) = a^2 D(X)\)。

方差

分布列同上。

对于上述分布列，方差 \(D(X) = \sum \limits_{i = 1}^n [x_i - E(X)]^2 p_i = [x_1 - E(x)]^2 p_1 + [x_2 - E(x)]^2 p_2 + \cdots + [x_n - E(x)]^2 p_n\)。

其中，\(\sqrt{D(X)}\) 叫做随机变量 \(X\) 的标准差。

性质：若 \(X\) 与 \(Y\) 都是随机变量，且 \(Y = aX + b(a \ne 0)\)，则 \(D(Y) = a^2 D(X)\)。

例题

例 1：某地政府为了帮助当地农民脱贫致富，开发了一种新型水果类食品，该食品产生成本为每件 \(8\) 元 。当天生产当天销售时，销售价为每件 \(12\) 元，当天未卖出的则只能卖给水果罐头厂，每件只能卖 \(5\) 元。每天的销售量与当地的气温（单位：\(\pu{^\circ C}\)）有关，根据市场调查，若气温不低于 \(30\)，则销售 \(5000\) 件；若气温位于区间 \([25,30)\)，则销售 \(3500\) 件；若气温低于 \(25\)，则销售 \(2000\) 件。为制定 2020 年 9 月份的生产计划，统计了前三年 9 月份的气温范围数据，得到下面的频数分布表：

气温范围（单位：\(\ce{^\circ C}\)）	\([15,20)\)	\([20,25)\)	\([25,30)\)	\([30,35)\)	\([35,40)\)
天数	4	14	36	21	15

以气温范围位于各区间的频率代替气温范围位于该区间的概率。

1. 求今年 9 月份这种产品一天销售量（单位：件）的分布列。
2. 设 9 月份一天销售这种食品的利润为 \(Y\)（单位：元），当 9 月份这种食品一天生产量 \(n\)（单位：件）为多少时，\(Y\) 的数学期望最大，最大值为多少？

求解：

对于第一问：

求出销售量所对应的概率即可，分布列如下：

\(X\)	\(2000\)	\(3500\)	\(5000\)
\(P\)	\(\dfrac 1 5\)	\(\dfrac 2 5\)	\(\dfrac 2 5\)

对于第二问：

由于产生量 \(n\) 值不同时，在不同的销售量下，得到的商品利润可能不同，所以需要对 \(n\) 分类讨论。

根据分布列中 \(X\) 的取值，可以将整个数轴分为四份，所以 \(n\) 也可以有四种分类讨论的情况，但当 \(n < 2000\) 和 \(n > 5000\) 时显然不可能利润达到最大，原因：

• 当 \(n < 2000\) 时，如果生产 \(2000\) 件，就有 \(2000\) 件能盈利，显然比 \(<2000\) 件盈利利润更大。
• 当 \(n > 5000\) 时，超过 \(5000\) 的部分一定要亏损，显然没有 \(n = 5000\) 时盈利更大。

所以只需要分类讨论 \(2000 < n \le 3500\) 和 \(3500 < n \le 5000\) 两种情况。

当 \(2000 < n \le 3500\) 时：

• 若 \(X = 2000\)，则 \(Y = 2000 \times 4 - 3(n - 2000) = -3n + 14000\)。
• 若 \(X = 3500\) 则 \(Y = 4n\)。
• 若 \(X = 5000\) 则 \(Y = 4n\)。

所以 \(E(Y) = \dfrac 1 5 (-3n + 14000) + \dfrac 2 5 \cdot 4n + \dfrac 2 5 \cdot 4n = \dfrac{13}{5} n + 2800 \le \dfrac{13}{5} \times 3500 + 2800 = 11900\)。

当 \(3500 < n \le 5000\) 时：

• 若 \(X = 2000\)，则 \(Y = 2000 \times 4 - 3(n - 2000) = -3n + 14000\)。
• 若 \(X = 3500\)，则 \(Y = 3500\times 4 - 3(n - 3500) = -3n + 24500\)。
• 若 \(X = 5000\) 则 \(Y = 4n\)。

所以 \(E(Y) = \dfrac 1 5 (-3n + 14000) + \dfrac 2 5(-3n + 24500) + \dfrac 2 5 \cdot 4n = - \dfrac 1 5 n + 12600 < \dfrac 1 5 \times 3500 + 12600 = 11900\)。

所以 \(Y\) 数学期望的最大值是 \(11900\) 元。

总结：

• 在遇到类似本题的这种在不同情况下答案不同的题目，需要按情况分类讨论求解。
• 注意在分类讨论时可以排除一些显然不符合题意的选项，提高速度和减少运算量。

---

例 2：为落实立德树人根本任务，坚持五育并举全面推进素质教育，某学校举行了乒乓球比赛，其中参加男子乒乓球决赛的 12 名队员来自 3 个不同校区，三个校区的队员人数分别是 3,4,5。本次决赛的比赛赛制采用单循环方式，即每名队员进行 11 场比赛（每场比赛都采取 5 局 3 胜制），最后根据积分选出最后的冠军，积分规则如下：比赛中以 \(3:0\) 或 \(3:1\) 取胜的队员积 3 分，失败的队员积 0 分；而在比赛中以 \(3:2\) 取胜的队员积 2 分，失败的队员积 1 分。已知第 10 轮张三对抗李四，设每局比赛张三取胜的概率均为 \(p(0 < p < 1)\)。

1. 比赛结束后冠亚军（没有并列）恰好来自不同校区的概率是多少？
2. 第 10 轮比赛中，记张三 \(3:1\) 取胜的概率为 \(f(p)\)。
   • 求出 \(f(p)\) 的最大值点 \(p_0\)。
   • 每局比赛张三取胜的概率均为 \(p = \dfrac 3 4\)。这轮比赛张三所得积分为 \(X\)，求 \(X\) 的分布列及期望。

求解：

第一问由于没有告诉具体概率，考虑用事件数计算概率：

\[P = \dfrac{3 \times 4 \times 2 + 3 \times 5 \times 2 + 4 \times 5 \times 2}{12 \times 11} = \dfrac{47}{66} \]

注意：这里冠亚军不同，所以计算总事件数若使用排列组合，应该是 \(\mathrm A_{12}^2\) 而不是 \(\mathrm C_{12}^2\)，在计算目标事件数时每种情况也要 \(\times 2\)。

对于第二问：

第一小问：

由于张三 \(3:1\) 取胜，所以张三最后一局一定胜出，所以张三在前三局有两句胜出。

那么张三 \(3:1\) 取胜的概率为：

\[f(p) = \mathrm C_3^2 \cdot p^3 \cdot (1 - p) = -3p^4 + 3p^3,0 < p < 1 \]

求 \(f(p)\) 最大值点，考虑求导：

\[f'(p) = -12p^3 + 9p^2 = 3p^2(-4p + 3) \]

因为 \(3p^2 > 0\)，所以只需考虑 \(-4p + 3\) 的正负。那么令 \(-4p + 3 = 0\)，得 \(p = \dfrac 3 4\)。

所以当 \(p \in \left(0,\dfrac 3 4\right)\) 时，\(f'(p) > 0\)，此时 \(f(p)\) 单调递增；当 \(p \in \left(\dfrac 3 4, 1\right)\) 时，\(f'(p) < 0\)，此时 \(f(p)\) 单调递减。

所以 \(p_0 = \dfrac 3 4\)。

注意：在遇到含比赛的体育比赛时，在计算概率时有一个隐藏条件，即最后一局的胜负情况已经确定，在考虑概率时最后一局不需要考虑。

第二小问：

考虑算出每个可能的 \(X\) 对应的频率：

\[P(X = 3) = \left(\dfrac 3 4\right)^3 + \mathrm C_3^2 \cdot \left(\dfrac 3 4 \right)^3 \cdot \dfrac 1 4 = \dfrac{189}{256}\\ P(X = 2) = \mathrm C_4^2 \cdot \left(\dfrac 3 4\right)^3 \cdot \left(\dfrac 1 4\right)^2 = \dfrac{81}{512}\\ P(X = 1) = \mathrm C_4^2 \cdot \left(\dfrac{3}{4}\right)^2 \cdot \left(\dfrac 1 4\right)^3 = \dfrac{27}{512}\\ P(X = 0) = \left(\dfrac 1 4\right)^3 + \mathrm C_3^2 \cdot \dfrac 3 4 \cdot \left(\dfrac 1 4\right)^3 = \dfrac{13}{256} \]

那么根据概率求出分布列即可，这里不做赘述。

所以期望为：

\[E(X) = 0 \times \dfrac{13}{256} + 1 \times \dfrac{27}{512} + 2 \times \dfrac{81}{512} + 3 \times \dfrac{189}{256} = \dfrac{1323}{512} \]

---

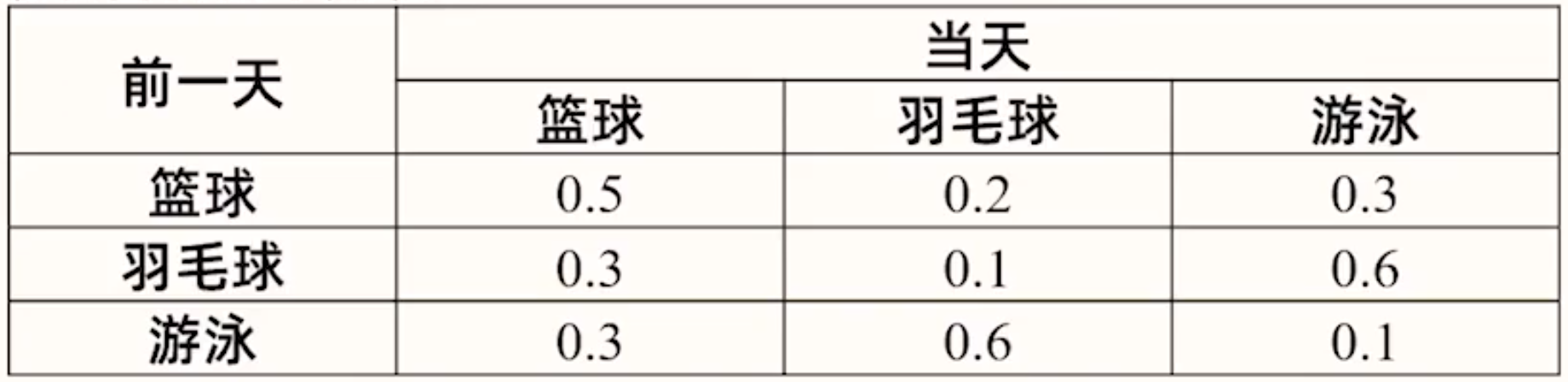
例 4：小王每天 \(17:00 - 18:00\) 都会参加一项自己喜欢的体育运动，运动项目有篮球、羽毛球、游泳三种，已知小王当天参加的运动项目只与前一天参加的运动项目有关，在前一天参加某类运动项目的情况下，当天参加各类运动项目的概率如表：

1. 已知小王第一天打羽毛球，则他第三天做哪项运动的可能性最大？

2. 已知小王参加三种体育运动一小时的能量消耗如表所示：

   

   求小王 从第一天打羽毛球开始，前三天参加体育运动能量消耗总数的分布列和期望。

求解：

对于第一问：

相当于要求出第三天做每项运动的概率然后做比较，总共有 \(3 \times 3 = 9\) 种情况，情况数较多，考虑树状图求解：

graph TB 1(羽毛球)---2(篮球)---3(篮球) 2(篮球)---4(羽毛球) 2(篮球)---5(游泳) 1(羽毛球)---6(羽毛球)---7(篮球) 6(羽毛球)---8(羽毛球) 6(羽毛球)---9(游泳) 1(羽毛球)---10(游泳)---11(篮球) 10(游泳)---12(羽毛球) 10(游泳)---13(游泳)

从左到右每种情况的概率：

• 羽毛球 - 篮球 - 篮球：\(0.3 \times 0.5 = 0.15\)。
• 羽毛球 - 篮球 - 羽毛球：\(0.3\times 0.2 = 0.06\)。
• 羽毛球 - 篮球 - 游泳：\(0.3 \times 0.3 = 0.09\)。
• 羽毛球 - 羽毛球 - 篮球：\(0.1\times 0.3 = 0.03\)。
• 羽毛球 - 羽毛球 - 羽毛球：\(0.1 \times 0.1 = 0.01\)。
• 羽毛球 - 羽毛球 - 游泳：\(0.1 \times 0.6 = 0.06\)。
• 羽毛球 - 游泳 - 篮球：\(0.6 \times 0.3 = 0.18\)。
• 羽毛球 - 游泳 - 羽毛球：\(0.6 \times 0.6 = 0.36\)。
• 羽毛球 - 游泳 - 游泳：\(0.6 \times 0.1 = 0.06\)。

所以

\[P(篮) = 0.15 + 0.03 + 0.18 = 0.36\\ P(羽) = 0.06 + 0.01 + 0.36 = 0.43\\ P(游) = 0.09 + 0.06 + 0.06 = 0.21 \]

所以第三天做羽毛球运动的可能性最大。

总结：对于这种有明显顺序且情况较多的概率题目，可以先通过树状图的方式将所有的情况都列举出来，然后再对每一种情况求解。

对于第二问：

可以考虑将每种情况消耗能量总数计算出来，然后将每个可能的能量结果对应的概率加起来求解。这里不做赘述。

二项分布

\(n\) 次独立重复试验（\(n\) 重伯努利试验）

将同一随机试验重复 \(n\) 次，每次试验是独立的，每次试验只有 \(2\) 种结果，每种结果的概率是不变的。

二项分布的定义

如果一次试验中，出现「成功」的概率为 \(p\)，且 \(n\) 次独立重复试验中出现「成功」的次数为 \(X\)，称 \(X\) 服从参数为 \(n,p\) 的二项分布，记作 \(X \sim B(n,p)\)，其中 \(X\) 的取值范围是 \(\{0,1,\cdots,k,\cdots,n\}\)。

则独立重复试验中出现 \(k\) 次成功的概率即为 \(P(X = k) = \mathrm C_n^k p^k(1 - p)^{n-k},k = 0,1,\cdots,n\)。这里的 \(\mathrm C_n^k\) 表示从 \(n\) 次试验重选择 \(k\) 次成功，即总情况数，\(p^k(1-p)^{n-k}\) 是每种情况下的概率。

二项分布求概率的一般方法：先找到随机变量 \(X\) 所有的取值，观察需要计算的概率对应到随机变量的哪些取值，然后用加法或减法计算概率（一般选择情况较少的一种方法）。

二项分布的期望和方差

若 \(X\) 服从参数为 \(n,p\) 的二项分布，即 \(X \sim B(n,p)\)，则 \(E(X) = np,D(X) = np(1 - p)\)。

注意：求解二项分布的数学期望时，一般首先要说明 \(X \sim B(n,p)\)。

求解有关二项分布的题型时，可以考虑表格法，即画出每一次独立试验和对应成功/失败的概率，观察分析求解。

例题

例 1：一袋中有 \(5\) 个白球，\(3\) 个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现 \(10\) 次时停止，设停止时共取了 \(X\) 次球，则 \(P(X = 12)\) 是多少。

分析：

题目求 \(P(X = 12)\) 相当于求当抽到第 \(12\) 次时，红球出现了 \(10\) 次，求抽到 \(12\) 次暂停的概率是多少。

由于当出现 \(10\) 次红球时停止，所以第 \(12\) 次一定抽到的是红球，所以只需要让前 \(11\) 次总共抽到 \(9\) 次红球，\(2\) 次白球，所以概率 \(P(X = 12) = \mathrm C_{11}^9 {\left(\dfrac{3}{8}\right)}^{10}\cdot {\left(\dfrac 5 8\right)}^2\)。

注意：此类题目虽然看起来与二项分布很像，但并不是二项分布，注意观察题目条件的区别，不要硬套。

---

例 2：国庆期间，某大型服装团购会举办了一次「你消费我促销」活动，顾客消费满 \(300\) 元（含 \(300\) 元）可抽奖一次，抽奖方案有两种（顾客只能选择其中的一种）。

方案一：从装有 \(5\) 个形状、大小完全相同的小球（其中红球 \(1\) 个，黑球 \(4\) 个）的抽奖盒中，有放回地摸出 \(3\) 个球，每摸出 \(1\) 次红球，立减 \(100\) 元。

方案二：从装有 \(10\) 个形状、大小完全相同的小球（其中红球 \(2\) 个，白球 \(1\) 个，黑球 \(7\) 个）的抽奖盒中，不放回的摸出 \(3\) 个球，中奖规则为：若摸出 \(2\) 个红球，\(1\) 个白球，则打 \(5\) 折；若摸出 \(1\) 个红球，\(1\) 个白球和 \(1\) 个黑球，则打 \(7.5\) 折；其余情况不打折。

求：

1. 某顾客恰好消费 \(300\) 元，选择抽奖方案一，求他实付金额的期望。
2. 若顾客消费 \(500\) 元，试从实付金额的期望值分析顾客选择何种抽奖方案更合理？

---

分析：

对于第一问：

设抽到 \(Y\) 次黑球，则 \(Y \sim B\left(3, \dfrac 4 5\right)\)，所以 \(E(Y) = 3 \times \dfrac 4 5 = \dfrac{12} 5\)。

设实付金额为 \(X\)，则根据题意可知随机变量 \(X = 100Y\)，所以 \(E(X) = 100 E(Y) = 100 \times \dfrac{12}{5} = 240\)。

总结：对于「有放回抽取」，有时转化为二项分布，那么求对应随机变量的期望，可以考虑看题目中要求的随机变量和二项分布的随机变量是否有关，如果有关系，就可以直接根据期望的性质直接得到所求的期望。

对于第二问：

设第一种方案实付金额为 \(\xi\) 元，第二种方案实付金额 \(\eta\) 元。

则由题意可知 \(\xi = 200 + X\)，所以根据第一问可知 \(E(\xi) = 200 + E(X) = 440\)。

对于第二种方案，考虑把每种实付金额的概率求出然后根据期望的定义求解，那么有：

\[P(\eta = 0) = \dfrac{\mathrm C_2^2 \cdot \mathrm C_1^1 \cdot \mathrm C_7^0}{\mathrm C_{10}^3} = \dfrac{1}{120}\\ P(\eta = 250) = \dfrac{\mathrm C_2^2 \cdot \mathrm C_1^0 \cdot \mathrm C_7^1}{\mathrm C_{10}^3} = \dfrac{7}{120}\\ P(\eta = 375) = \dfrac{\mathrm C_2^1 \cdot \mathrm C_1^1 \cdot \mathrm C_7^1}{\mathrm C_{10}^3} = \dfrac{7}{60}\\ P(\eta = 500) = 1 - \dfrac{1}{120} - \dfrac{7}{120} - \dfrac{7}{60} = \dfrac{49}{60} \]

那么期望为：

\[E(\eta) = 0 \times \dfrac{1}{120} + 250 \times \dfrac{7}{120} + 375 \times \dfrac{7}{60} + 500 \times \dfrac{49}{60} = 466 \dfrac 2 3 \]

因为 \(440 < 466 \dfrac 2 3\)，所以第一种抽奖方案更合理。

超几何分布

一般地，若有总数为 \(N\) 件的甲、乙两类物品，其中甲类 \(M\) 件（\(M < N\)），从所有物品中随机取出 \(n\) 件（\(n \le N\)），则这 \(n\) 件中所含甲类物品数 \(X\) 是一个离散型随机变量，称 \(X\) 服从参数为 \(N,n,M\) 的超几何分布，且 \(E(X) = \dfrac{nM}{N}\)。

直观理解：两类物品，每类物品的数量确定，从两类物品中共抽出固定数量的物品，\(X\) 是抽出的物品中其中一类的数量，则 \(X\) 的期望 \(=\) 抽出的数量 \(\times\) 这类物品的比例，一般概率利用组合数计算。

超几何分布计算概率一般可用 目标事件数除以总事件数 计算，求分布列可以列出所有随机变量 \(X\) 可能的情况，再将每一种情况的概率计算求得。

二项分布与超几何分布的区别

二项分布：多次试验，每次试验有两种结果，每种结果的概率确定。

超几何分布：两类物品取固定数量，每类物品的数量确定。

简单来说，二项分布是有放回的抽取，而超几何分布是一次性抽取。

核心区别：

• 二项分布：概率确定，数量不确定，所以一般用概率计算概率。
• 超几何分布：数量确定，概率不确定，所以一般用事件数计算概率。

例如：扔 \(100\) 次硬币，正面朝上和朝下的概率都是 \(\dfrac 1 2\)（概率确定），但正面朝上和朝下的具体数量不确定，这就属于二项分布；\(50\) 名男生，\(50\) 名女生，从中选 \(40\) 人（数量确定），每次选到男生女生的概率不确定，这就属于超几何分布。

---

例：某精准扶贫帮扶单位，为帮助顶点扶贫村真正脱贫，坚持扶贫同扶智相结合，帮助精准扶贫户利用互联网电商渠道销售当地特产苹果。苹果单果直径不同单价不同，为了更好地销售，现从该精准扶贫户种植的苹果树上随机摘下 \(50\) 个苹果测量其直径，经统计，其单果直径分布在区间 \([50,95]\) 内（单位：\(\pu{mm}\)），统计地茎叶图如图所示：

以此茎叶图中单果直径出现的频率代表概率，直径位于 \([65,90)\) 内的苹果称为优质苹果，对于该精准扶贫户的这批苹果，某电商提出两种收购方案：

方案 A：所有苹果均以 \(5\) 元/千克收购；

方案 B：从这批苹果中随机抽取 \(3\) 个苹果，若都是优质苹果，则按 \(6\) 元/千克收购；若有 \(1\) 个非优质苹果， 则按 \(5\) 元/千克收购；若有 \(2\) 个非优质苹果，则按 \(4.5\) 元/千克收购；若有 \(3\) 个非优质苹果，则按 \(4\) 元/千克收购。

请你通过计算为该精准扶贫户推荐最好的方案。

---

分析：

所谓最好的方案，就是将方案 A 的苹果单价与方案 B 的期望苹果单价作比较，然后选择苹果单价更高的作为最好方案。

由于方案 A 的苹果单价已知，那么问题转化为计算方案 B 的期望苹果单价。

观察题目可知，方案 B 是从这批苹果中随机抽取 \(3\) 个苹果，并不是从题目茎叶图已知的 \(50\) 个苹果中抽取 \(3\) 个，所以相当于数量不确定，又由于题目告诉了让用频率代表概率，所以相当于概率确定；又由于这批苹果的基数很大，所以抽取 \(1\) 个苹果后不放回对抽取下一个苹果的概率影响极小，所以综合而言，可以近似认为它属于二项分布。

那么将茎叶图中的 \(50\) 个苹果的直径分为在 \([65,90)\) 内和不在 \([65,90)\) 内的，发现有 \(40\) 个优质苹果，\(10\) 个非优质苹果，所以可以认为优质苹果的概率为 \(\dfrac 4 5\)，非优质苹果的概率为 \(\dfrac 1 5\)。设 B 方案的收购价格为 \(X\)，则：

\[P(X = 6) = {\left(\dfrac 4 5\right)}^3 = \dfrac{64}{125}\\ P(X = 5) = \mathrm C_3^2 \cdot {\left(\dfrac 4 5\right)}^2 \cdot \dfrac 1 5 = \dfrac{48}{125}\\ P(X = 4.5) = \mathrm C_3^1 \cdot \left(\dfrac 4 5\right) \cdot {\left(\dfrac 1 5\right)}^2 = \dfrac{12}{125}\\ P(X = 4) = {\left(\dfrac 1 5\right)}^3 = \dfrac 1 {125} \]

由于二项分布的期望计算公式里的 \(X\) 表示的是某种结果出现的次数，不适用于这里的收购价格，那么需要使用期望的定义求解。

则

\[E(X) = 6 \times \dfrac{64}{125} + 5 \times \dfrac{48}{125} + 4.5 \times \dfrac{12}{125} + 4 \times \dfrac 1 {125} = 5.456 > 5 \]

推荐方案 B。

总结：

此类题目的特点：从全体中抽取一部分样本，已知样本数据。

如果题目是从样本中抽取几个，则样本数量确定，属于超几何分布，用事件数计算概率。

如果题目是从全体中抽取几个，且已知「用频率代替概率」，则属于二项分布，用概率（频率）计算概率。

条件概率

定义

条件概率是指事件 \(A\) 在另外一个事件 \(B\) 已经发生条件下的发生概率，用 \(P(A|B)\) 表示，有

\[P(A|B) = \dfrac{P(AB)}{P(B)} \]

条件概率与二者同时发生的概率的区别：样本空间不同，即总事件数不同。前者样本空间应该取条件发生对应的所有情况，而后者是整体上所有可能的情况。

注意：在题目中，要善于识别有些条件概率。例如「前一球投进则后一球投不进的概率」就是条件概率，即在前一球投进的条件下后一球投不进的概率，而「前一球投进且后一球投不进的概率」并非条件概率，而是二者同时发生的概率。

计算方法

法一：利用事件数计算。即在事件 \(B\) 发生的前提下，找到目标事件数和总事件数，用 \(\dfrac{目标事件数}{总事件数}\) 计算。

法二：利用概率计算概率。即利用公式 \(P(A|B) = \dfrac{P(AB)}{P(B)}\) 分别计算 \(P(B)\) 和 \(P(AB)\) 然后再代入公式计算。

适用范围

有三种情况：

1. 直接求 \(P(A|B)\)。
2. 题目中存在「在……条件下」之类的字眼：可以将给定条件直接看成条件 \(B\)，求条件概率。
3. 题目中存在「已知……」之类的字眼：可以将已知的对象看成条件 \(B\)，求条件概率。

【题型】纯概率计算问题

主要公式：

\[P(A) + P(\overline A) = 1\\ P(A | B) = \dfrac{P(AB)}{P(B)}\\ P(AB) + P(A\overline B) = P(A) \]

注意：不能使用公式 \(P(AB) = P(A)\cdot P(B)\)，该公式只对独立事件适用。

思路：利用上述的三个公式转化求解即可。

有些看上去非纯概率问题也可以转化为纯概率来求解，在某些问题中如果搞不清楚概率之间的逻辑关系，可以设出题目中的事件为事件 \(A\) 或事件 \(B\)，利用字母转化成概率的数学表达式，再利用纯概率计算的方法求解。

例题

例：现有 \(5\) 名同学站在一排拍照毕业留念，在「甲不站在最左边，乙不站在最右边」的前提下，丙站在最左边的概率是多少？

求解：

考虑利用公式 \(P(A|B) = \dfrac{P(AB)}{P(B)}\) 求解。由于 \(P(AB)\) 和 \(P(B)\) 的样本空间（总事件数）都相同，所以在计算时一定会约掉，所以可以只计算上下两种情况的目标事件数求解。

设「丙站在最左边」是事件 \(A\)，「甲不站在最左边，乙不站在最右边」是事件 \(B\)。

那么 \(B\) 发生时，有两种情况：甲不站在最右边，此时乙有 \(3\) 种选择的情况，总共有 \(3 \times 3\) 种情况；甲站在最右边，此时乙有 \(4\) 种选择的情况，总共有 \(1 \times 4\) 种情况。然后其余三人随便站，那么总共有 \((3 \times 3 + 1 \times 4) \cdot \mathrm A_3^3 = 78\) 种情况。

\(AB\) 同时发生时，丙的位置已经确定，乙不站在最右边有 \(3\) 种情况，然后剩下三人随便站，那么总共有 \(3 \times \mathrm A_3^3 = 18\) 种情况。

所以此题总概率为 \(\dfrac{18}{78} = \dfrac{3}{13}\)。

总结：利用公式 \(P(A|B) = \dfrac{P(AB)}{P(B)}\) 求解时，由于 \(P(AB)\) 和 \(P(B)\) 的样本空间（总事件数）都相同，所以在计算时一定会约掉，所以可以只计算上下两种情况的目标事件数求解。

全概率公式与贝叶斯公式

定义

一般地，设 \(A_1,A_2,\cdots,A_n\) 是一组两两互斥的事件，\(A_1 \cup A_2 \cup \cdots \cup A_n = \Omega\)，且 \(P(A_i) > 0\)，\(i = 1,2, \cdots,n\)，则对任意的事件 \(B \subseteq \Omega\)，有：

\[P(B) = \sum \limits_{i = 1}^n P(A_i) P(B | A_i)\\ P(A_i|B) = \dfrac{P(A_i) P(B|A_i)}{\sum \limits_{k = 1}^n P(A_k) P(B | A_k)} \]

前者是全概率公式，后者是贝叶斯公式。

适用范围：要完成的某一件事需要做分类。

求解方法：可以找到题目中的多类情况，用树状图表示，然后计算结果，套上对应的公式求解。

对于两种公式的理解

对于全概率公式的理解：

若某一步的不同选择会对下一步的概率有影响，那么从这一步开始需要分类求解，然后将每一类的概率相加就是总的概率，即 \(P(B) = \sum P(每一种情况)\)。每一类情况中，将每种情况本身的概率乘上这种情况下得到结果的概率，就是这一类情况的概率，即 \(P(每一种情况) = P(A_i) P(B | A_i)\)。

对于贝叶斯公式的理解：

贝叶斯公式求的是某种结果已经发生的情况下，这种结果在某种情况发生的概率，属于条件概率，即 \(P(A_i | B)\)。所以可以用第 \(i\) 种情况的概率除以所有情况发生的总概率，而前者即为 \(P(A_i) P (B|A_i)\)，后者即为全概率。

全概率公式与贝叶斯公式的区别与联系：

二者在求概率的过程中都需要分类，而全概率公式一般求的是最终结果的概率，而如果题目告诉最终结果已经发生，在最终结果发生的情况下求结果发生的情况的概率，属于条件概率，则需要使用贝叶斯公式。即全概率是根据原因推结果（各种情况的概率相加），贝叶斯公式是根据结果找原因（这种原因的概率除以总概率）。

线性回归方程

引入

线性回归方程的目标：建立两个变量间（近似）的函数关系。

建立思路：

1. 分析函数类型：根据图像变化趋势猜测函数类型，例如一次函数就是 \(\widehat y = \widehat b x + \widehat a\)。
2. 明确目标：利用 \(x_1,x_2,\cdots,x_n\) 和 \(y_1,y_2,\cdots,y_n\) 求出 \(\widehat b,\widehat a\)。
3. 确定算法：依据是使得误差最小，总误差为每个误差的平方之和。算法是最小二乘法。
4. 得到公式。

计算公式：

\[\widehat b = \dfrac{\sum_{i = 1}^n (x_i - \overline x)(y_i - \overline y)}{\sum_{i = 1}^n(x_i - \overline x)^2} = \dfrac{\sum_{i = 1}^n x_iy_i - n \overline x \cdot \overline y}{\sum_{i = 1}^n {x_i}^2 - n {\overline x}^2}\\ \widehat a = \overline y - \widehat b \overline x \]

注意：计算公式不用记忆，考场上只要会两个公式之间的推导就行。

小结论：根据 $\widehat a $ 的计算公式变形可得到 \(\overline y = \widehat b \overline x + \widehat a\)，所以线性回归方程一定经过点 \((\overline x,\overline y)\)。

线性回归方程的作用：做预测，即在求出近似函数关系后，例如 \(\widehat y = \widehat b x + \widehat a\) 给定一个 \(x\) 的值，可以求出 \(y\) 的预测值。

公式推导（从 \(\widehat b\) 的第一个公式推导到第二个公式）：

\[\begin{aligned} \widehat b & = \dfrac{\sum_{i = 1}^n (x_i - \overline x)(y_i - \overline y)}{\sum_{i = 1}^n(x_i - \overline x)^2}\\ & = \dfrac{\sum_{i = 1}^n x_i y_i - \overline y \sum_{i = 1}^n x_i - \overline x \sum_{i = 1}^n y_i + n\overline x \cdot \overline y}{\sum_{i = 1}^n {x_i}^2 -2\overline x \sum_{i = 1}^n x_i + n {\overline x}^2}\\ & = \dfrac{\sum_{i = 1}^n x_i y_i - n \overline x \cdot \overline y - n \overline x \cdot \overline y + n\overline x \cdot \overline y}{\sum_{i = 1}^n {x_i}^2 -2n{\overline x}^2 + n {\overline x}^2}\\ & = \dfrac{\sum_{i = 1}^n x_iy_i - n \overline x \cdot \overline y}{\sum_{i = 1}^n {x_i}^2 - n {\overline x}^2}\\ \end{aligned}\\ \]

常见的非线性模型

非线性函数往往能转化为线性函数。

常见的非线性模型转化：

1. 对于 \(y = a\ln x + b\)，可以设 \(u = \ln x\)，则 \(y = au + b\)。
2. 对于 \(y = \ln (ax + b)\)，遇到对数可以两边取 \(e^x\)，即 \(e^y = ax + b\)，设 \(v = e^y\)，则 \(v = ax + b\)。
3. 对于 \(y = ke^{mx}(k,m > 0)\)，遇到指数可以两边取对数，即 \(\ln y = \ln (ke^{mx}) = \ln k + \ln e^{mx} = \ln k + mx\)。设 \(t = \ln y\)，则 \(t = mx + \ln k\)。

相关系数 \(r\)

相关系数 \(r\) 是衡量两个变量间的线性相关程度的量，计算公式题目往往会直接给出，不需要记忆（这里就不写了），\(r\) 的大小与两个变量线性相关程度的关系：

• 若 \(r>0\)，则两个变量呈正相关。
• 若 \(r < 0\)，则两个变量呈负相关。
• \(|r|\) 越接近 \(1\)，则两个变量线性相关性越强，即越适合用一次函数的线性回归方程来表示。
• \(|r|\) 越接近 \(0\)，则两个变量几乎不存在线性关系，即越不适合用一次函数的线性回归方程表示。

决定系数 \(R^2\)

计算公式：

\[R^2 = 1 - \dfrac{\sum_{i = 1}^n (y_i - \widehat{y_i})^2}{\sum_{i = 1}^n (y_i - \overline y)^2} \]

右边式子中分式部分，分子中 \(y_i - \widehat{y_i}\) 叫做残差，分子上的 \(\sum_{i = 1}^n (y_i - \widehat{y_i})^2\) 叫做残差平方和。

决定系数与线性回归模型的关系：

• \(R^2\) 越大 \(\to\) 残差平方和越小 \(\to\) 模型的拟合效果越好。
• \(R^2\) 越小 \(\to\) 残差平方和越大 \(\to\) 模型的拟合效果越差。

可类比误差来看待决定系数。

独立性检验

研究方法：

1. 列 \(2 \times 2\) 联表。
2. 计算随机变量 \(K^2\)：\(K^2\) 的计算公式往往题目会直接给出，直接套公式即可，其中 \(n\) 为样本容量（调查总数）。新高考还需要写出零假设 \(H_0\)（两件事情无关）。
3. 解读结果：\(K^2\) 越大，两件事情有关的可能性越大，无关的可能性越小。

对于第三步解读结果的示例：

例如，题目告诉若两件事无关，则 \(P(K^2 \ge 6.635) \approx 0.01\)，则说明当 \(K^2 \ge 6.635\) 时两件事无关的概率约等于 \(0.01\)，一般有以下几种问法：

• 是否有（至少）\(99\%\) 的把握认为两件事有关：若 \(K^2 \ge 6.635\) 则有，反之则无。
• 是否在犯错概率（不超过）\(0.01\) 的前提下认为两件事有关：这里的犯错概率就是两件事无关的概率，所以答案同上。
• 依据小概率值 \(\alpha = 0.01\) 的独立性检验，能否认为两件事有关：这里的小概率值就是两件事无关的概率，答案同上。

特别注意：题目给的概率都是「无关」的概率。

对于解题过程中零假设 \(H_0\) 的书写：

1. 写出零假设 \(H_0\)：\(X\) 与 \(Y\) 无关联。
2. 计算 \(K^2\) 并与对应的 \(\alpha\) 比较。
3. 写出结论：
   • 若 \(K^2 > a\)：根据小概率值 \(\alpha = \cdots\) 的独立性检验，推断 \(H_0\) 不成立，即 \(X\) 与 \(Y\) 有关联。
   • 若 \(K^2 < a\)：根据小概率值 \(\alpha = \cdots\) 的独立性检验，推断 \(H_0\) 成立，即 \(X\) 与 \(Y\) 无关联。

正态分布

定义

生活中，很多变量符合中间多、两头少、对称分布的特点，正态分布可以描述有这种特点的变量。比如：身高、体重、考试成绩等。

注意：正态分布描述的对象一般是连续的实数。

利用正态分布求概率

【第一步：读懂正态分布表示】

题目中会给出 \(X \sim N(\mu,\sigma^2)\)，说明随机变量 \(X\) 服从正态分布。

其中 \(\mu\) 表示 \(X\) 的期望，\(\sigma^2\) 表示 \(X\) 的方差。

【第二步：找概率条件并翻译】

找到题目中表示概率的式子，并代入你写好的 \(\mu\) 和 \(\sigma\)。

例如常见数据（题目会给出）：

\[P(\mu - \sigma < X < \mu + \sigma) \approx 0.6827\\ P(\mu - 2\sigma < X < \mu + 2\sigma) \approx 0.9545\\ P(\mu - 3\sigma < X < \mu + 3\sigma) \approx 0.9973 \]

【第三步：画图表示概率并解决问题】

画图时需要注意：对称轴是 \(x = \mu\)，即图像关于 \(x = \mu\) 对称，根据图像可求出 \(P(X \le \mu) = P(X \ge \mu) = 0.5\)。

根据第二步中求出的概率，可以根据对称轴的特性，计算出其它概率，例如已知 \(P(\mu - \sigma < X < \mu + \sigma) \approx 0.68\)，则 \(P(\mu - \sigma < X < \mu) = P(\mu < X < \mu + \sigma) = 0.34\)。