二分板子

整数二分

在单增序列中寻找 $\geq x$ 的数中最小的一个, 即若有多个相同的 $x$ 则找到最前面的那个若没有 $x$ 则找到 $\geq x$ 的最小的那个

while(l < r) {
        int mid = l + r >> 1;       //取不到r
        if(a[mid] >= x) r = mid;    //x在左半边
        else    l = mid + 1;
    }
    return l;       //最后l == r
}

 在单增序列中寻找 $\leq x$ 的最大的一个, 即若有多个相同的 $x$ 则找到最后面的那个若没有 $x$ 则找到 $\leq x$ 的最大的那个

while(l < r) {
        int mid = l + r + 1 >> 1;   //取不到l
        if(a[mid] <= x) l = mid;    //x在左半边
        else    r = mid - 1;
    }
    return l;
}

两个板子处理无解的情况($x$比最小的还小或比最大的还大)

板1:　找后继, $x$ 比最大的还大是无解情况, 将二分区间 $[1, n]$ 改为 $[1, n + 1]$, 若返回 $n + 1$ 则无解

板2:　找前驱, $x$ 比最小的还小是无解情况, 将二分区间 $[1, n]$ 改为 $[0, n]$, 若返回 $0$ 则无解

 

 二分答案

最优化问题的"值域"往往具有特殊的单调性——两段性, 即一段合法而另一段不合法, 借助二分, 我们可以找到两段区间的端点, 即答案

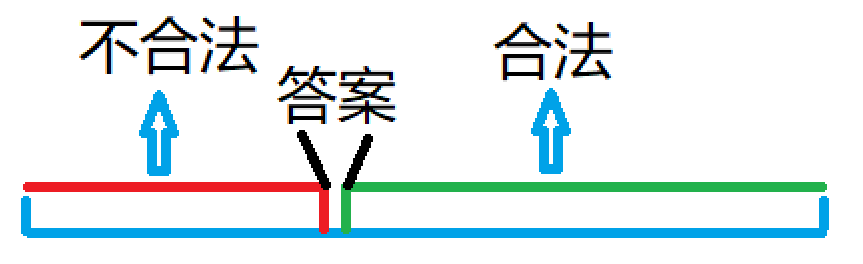
所以我们只需要将整数二分的板子稍加修改, 即将大小的判断转换为合法性的判断

while(l < r) {
        int mid = l + r >> 1;
        if(check(mid)) r = mid;    //检查mid的合法性, 右半段都合法
        else    l = mid + 1;
    }
    return l;       //最后l == r
}

 

浮点数二分

确定好所需的精度, 一般精确到题设再后两位, 如保留 $k$ 位小数时, 选取精度 $eps = 10 ^ {-(k+2)}$

while(r - l > eps) {
    double mid = (l + r) / 2;
    if(cal(mid)) r = mid;
    else l = mid;
}

当精度不容易表示时, 直接干脆循环固定次数(如100次)

for(int i = 0; i < 100; i++) {
    double mid = (l + r) / 2;
    if(cal(mid)) r = mid;
    else l = mid;
}