代码随想录算法Day31 | 455.分发饼干 ，376. 摆动序列 ，53. 最大子序和

455.分发饼干

题目链接：455. 分发饼干 - 力扣（LeetCode）

思路

这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

也可以换一个思路，小饼干先喂饱小胃口。

代码

class Solution {
    // 思路1：优先考虑饼干，小饼干先喂饱小胃口
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int start = 0;
        int count = 0;
        for (int i = 0; i < s.length && start < g.length; i++) {
            if (s[i] >= g[start]) {
                start++;
                count++;
            }
        }
        return count;
    }
}

class Solution {
    // 思路2：优先考虑胃口，先喂饱大胃口
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int count = 0;
        int start = s.length - 1;
        // 遍历胃口
        for (int index = g.length - 1; index >= 0; index--) {
            if(start >= 0 && g[index] <= s[start]) {
                start--;
                count++;
            }
        }
        return count;
    }
}

 

376. 摆动序列

题目链接：376. 摆动序列 - 力扣（LeetCode）

思路

 

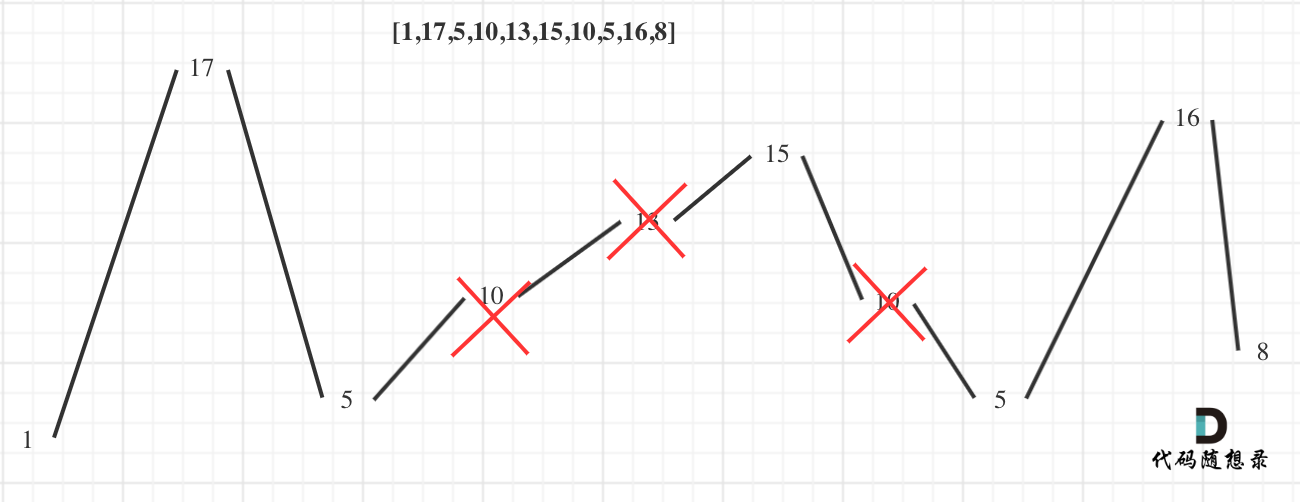
首先可以将题目给的数据画出如上的波峰图，根据图中可知：

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

在实际操作可以设置一个遍历记录峰值数量就可以了。

 当用这思路解决该问题时要注意三个问题。

• 当仅有两个数字，当两个数字不相等时，是2个峰
• 当仅有一个数字时，是1个峰
• 当有N个数字，但是这N个数字值都相同时，也算1个峰

代码

class Solution {
    public int wiggleMaxLength(int[] nums) {
        if (nums.length <= 1) {
            return nums.length;
        }
        //当前差值
        int curDiff = 0;
        //上一个差值
        int preDiff = 0;
        int count = 1;
        for (int i = 1; i < nums.length; i++) {
            //得到当前差值
            curDiff = nums[i] - nums[i - 1];
            //如果当前差值和上一个差值为一正一负
            //等于0的情况表示初始时的preDiff
            if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
                count++;
                preDiff = curDiff;
            }
        }
        return count;
    }
}

// DP
class Solution {
    public int wiggleMaxLength(int[] nums) {
        // 0 i 作为波峰的最大长度
        // 1 i 作为波谷的最大长度
        int dp[][] = new int[nums.length][2];

        dp[0][0] = dp[0][1] = 1;
        for (int i = 1; i < nums.length; i++){
            //i 自己可以成为波峰或者波谷
            dp[i][0] = dp[i][1] = 1;

            for (int j = 0; j < i; j++){
                if (nums[j] > nums[i]){
                    // i 是波谷
                    dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
                }
                if (nums[j] < nums[i]){
                    // i 是波峰
                    dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
                }
            }
        }

        return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);
    }
}

 

53. 最大子序和

题目链接：53. 最大子数组和 - 力扣（LeetCode）

思路

暴力解法的思路，第一层for 就是设置起始位置，第二层for循环遍历数组寻找最大值。

而贪心的方法，从第一个数开始累加，如果当前和已经为负，那么加上下一个数，一定会使下一个数变小。所以出现这种情况时，直接舍弃这个数，从下一个数开始重新计算。

详细如图

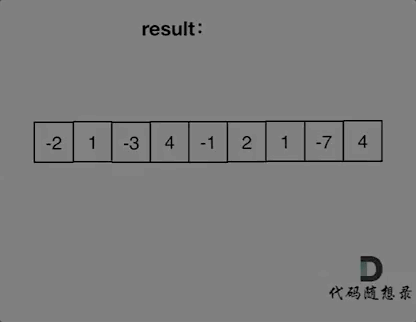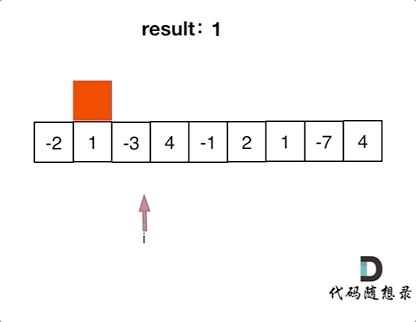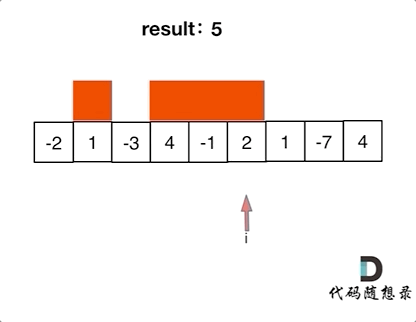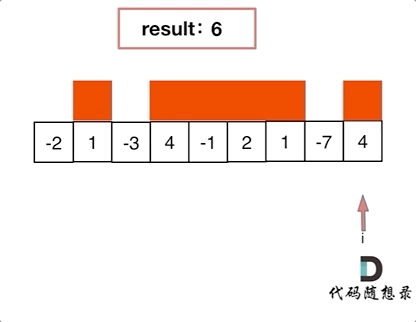
代码

class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 1){
            return nums[0];
        }
        int sum = Integer.MIN_VALUE;
        int count = 0;
        for (int i = 0; i < nums.length; i++){
            count += nums[i];
            sum = Math.max(sum, count); // 取区间累计的最大值（相当于不断确定最大子序终止位置）
            if (count <= 0){
                count = 0; // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
            }
        }
       return sum;
    }
}

// DP 方法
class Solution {
    public int maxSubArray(int[] nums) {
        int ans = Integer.MIN_VALUE;
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        ans = dp[0];

        for (int i = 1; i < nums.length; i++){
            dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);
            ans = Math.max(dp[i], ans);
        }

        return ans;
    }
}