代码随想录算法Day29 | 491.递增子序列 ，46.全排列 ，47.全排列 II

 

491.递增子序列

题目链接：491. 递增子序列 - 力扣（LeetCode）

思路

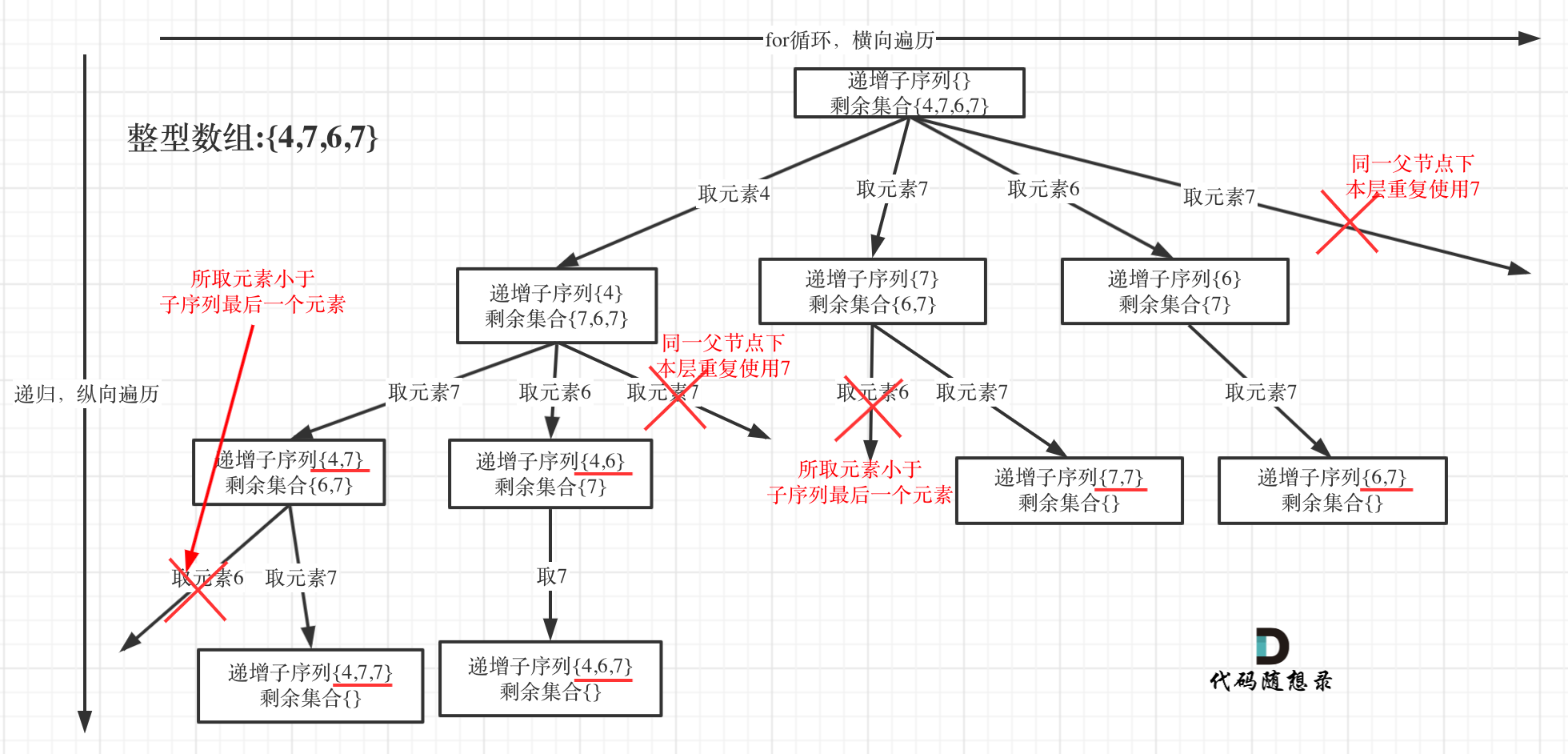
这道题和 90.集合II 类似。不同的是这道题不能通过排序使相同元素聚集在一起，因此不能使用 used数组 或者 startIndex 的方法去重。

在这道题中，虽然我们不可以让相同元素聚集在一起，但是我们可以通过 map 或 数组来当哈希（题目数值范围[-100,100]）来记录当前

树层已经是否已经使用该元素。

注意，进入新一层的时候要重新定义（清空），map 或 数组当哈希 只负责记录本次是否已经访问过。

详细如图所示。

 

 

代码

// 使用数组当map
class Solution {
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums,0);
        return res;
    }

    private void backtracking (int[] nums, int start) {
        if (path.size() > 1) {
            res.add(new ArrayList<>(path));
        }

        int[] used = new int[201];
        for (int i = start; i < nums.length; i++) {
            if (!path.isEmpty() && nums[i] < path.get(path.size() - 1) ||
                    (used[nums[i] + 100] == 1)) continue;
            used[nums[i] + 100] = 1;
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

//法二：使用map
class Solution {
    //结果集合
    List<List<Integer>> res = new ArrayList<>();
    //路径集合
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        getSubsequences(nums,0);
        return res;
    }
    private void getSubsequences( int[] nums, int start ) {
        if(path.size()>1 ){
            res.add( new ArrayList<>(path) );
            // 注意这里不要加return，要取树上的节点
        }
        HashMap<Integer,Integer> map = new HashMap<>();
        for(int i=start ;i < nums.length ;i++){
            if(!path.isEmpty() && nums[i]< path.getLast()){
                continue;
            }
            // 使用过了当前数字
            if ( map.getOrDefault( nums[i],0 ) >=1 ){
                continue;
            }
            map.put(nums[i],map.getOrDefault( nums[i],0 )+1);
            path.add( nums[i] );
            getSubsequences( nums,i+1 );
            path.removeLast();
        }
    }
}

 

46.全排列

题目链接：46. 全排列 - 力扣（LeetCode）

思路

首先通过题意可知排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

因此每次循坏都要从零开始，而在遍历的时候就需要 “树枝去重”。

树枝去重关键点在于used数组的使用。在used数组中 我们把上层已经遍历过的元素 记为 true ，因此在遍历的时候

只要used数组为true，就直接进入到下一层。

具体过程如下

 

 

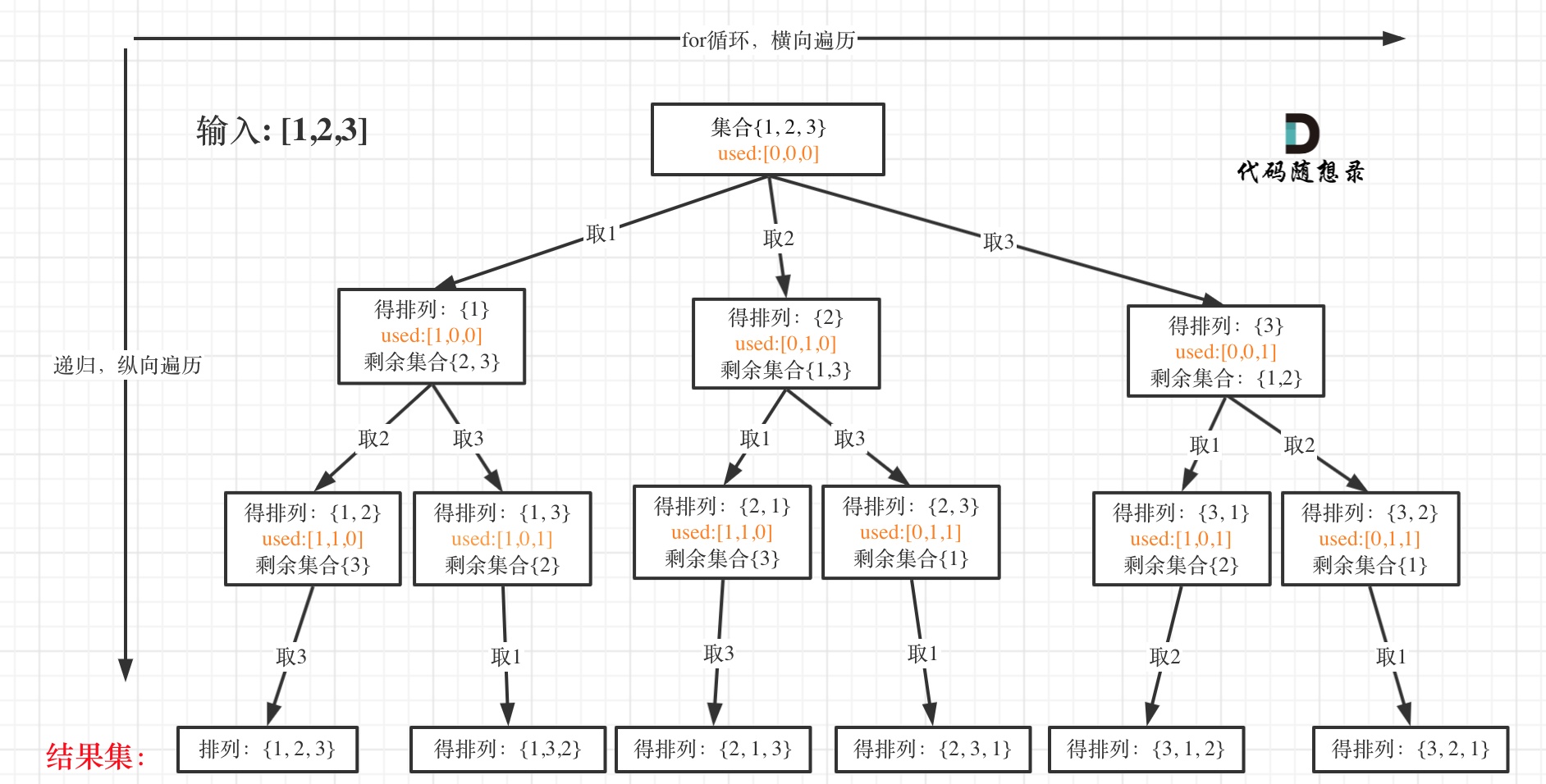
注意，回溯的时候也要把used一并回溯。

代码

// 使用used数组
class Solution {

    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0){
            return result;
        }
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }

    private void permuteHelper(int[] nums){
        if (path.size() == nums.length){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++){
            if (used[i]){
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

// 解法2：通过判断path中是否存在数字，排除已经选择的数字
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0) return result;
        backtrack(nums, path);
        return result;
    }
    public void backtrack(int[] nums, LinkedList<Integer> path) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
        }
        for (int i =0; i < nums.length; i++) {
            // 如果path中已有，则跳过
            if (path.contains(nums[i])) {
                continue;
            } 
            path.add(nums[i]);
            backtrack(nums, path);
            path.removeLast();
        }
    }
}

 

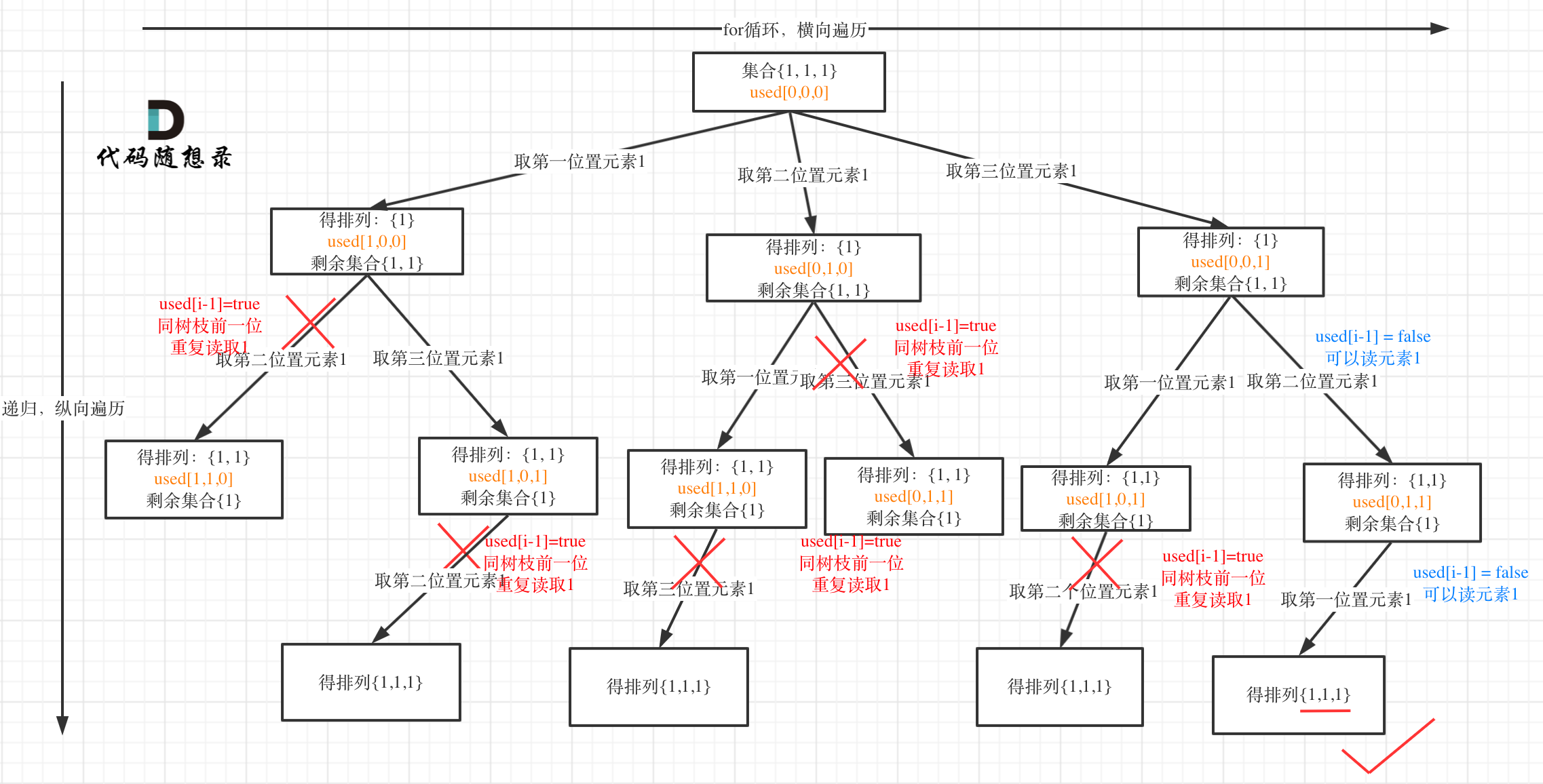
47.全排列 II

题目链接：46. 全排列 - 力扣（LeetCode）

思路

这道题与上面一题大致，区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

因此这道题需要用到 “树层去重” 和 “树枝去重” 。

详细过程如下

 

 

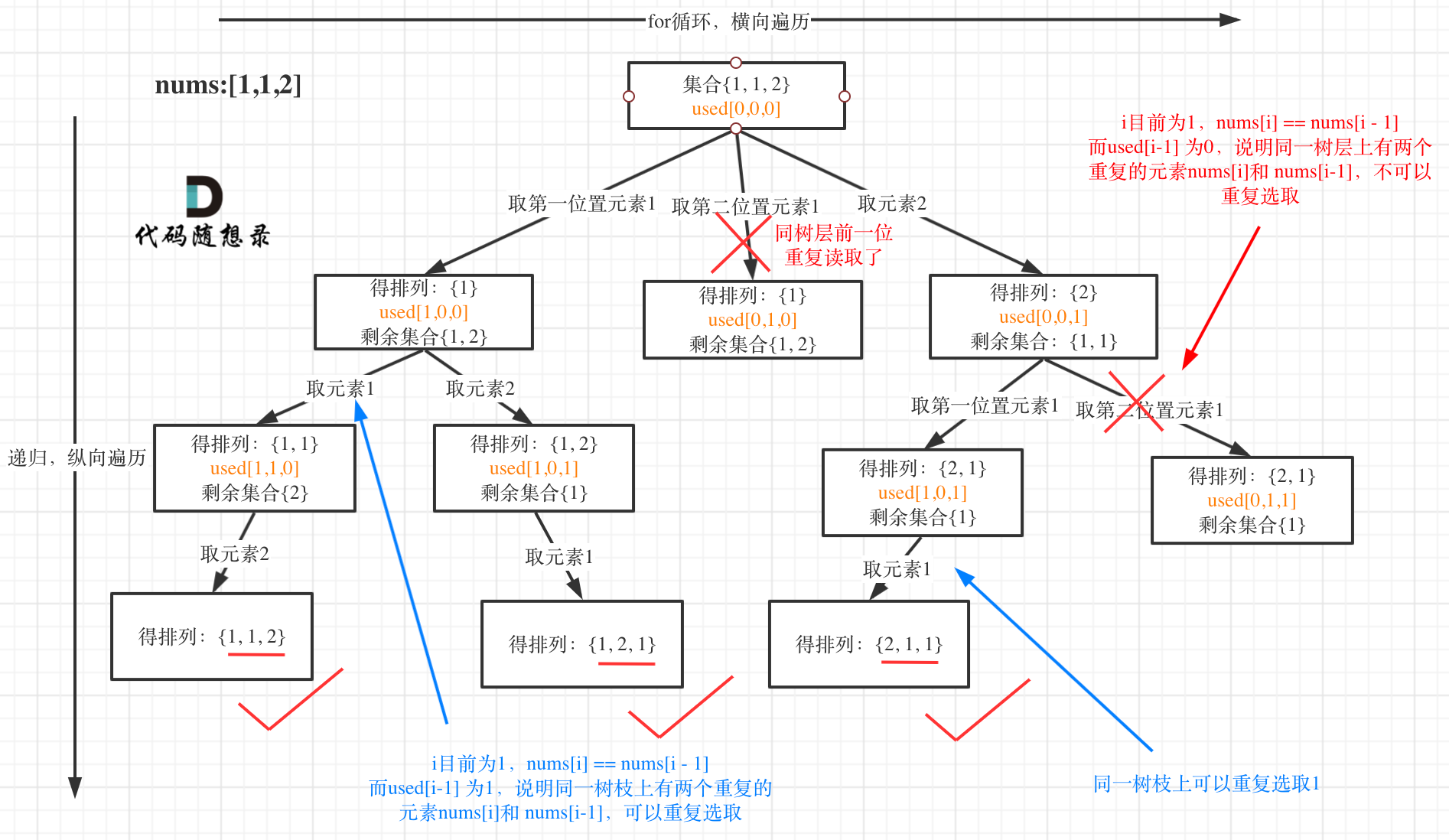
注意：这里去重的时候一定要先对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

代码

class Solution {
    //存放结果
    List<List<Integer>> result = new ArrayList<>();
    //暂存结果
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length];
        Arrays.fill(used, false);
        Arrays.sort(nums);
        backTrack(nums, used);
        return result;
    }

    private void backTrack(int[] nums, boolean[] used) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过
            // used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过
            // 如果同⼀树层nums[i - 1]使⽤过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            //如果同⼀树⽀nums[i]没使⽤过开始处理
            if (used[i] == false) {
                used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树枝重复使用
                path.add(nums[i]);
                backTrack(nums, used);
                path.remove(path.size() - 1);//回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复
                used[i] = false;//回溯
            }
        }
    }
}

扩展

这道题去重的关键在于

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

如果改成 used[i - 1] == true， 也是正确的!，去重代码如下：

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
    continue;
}

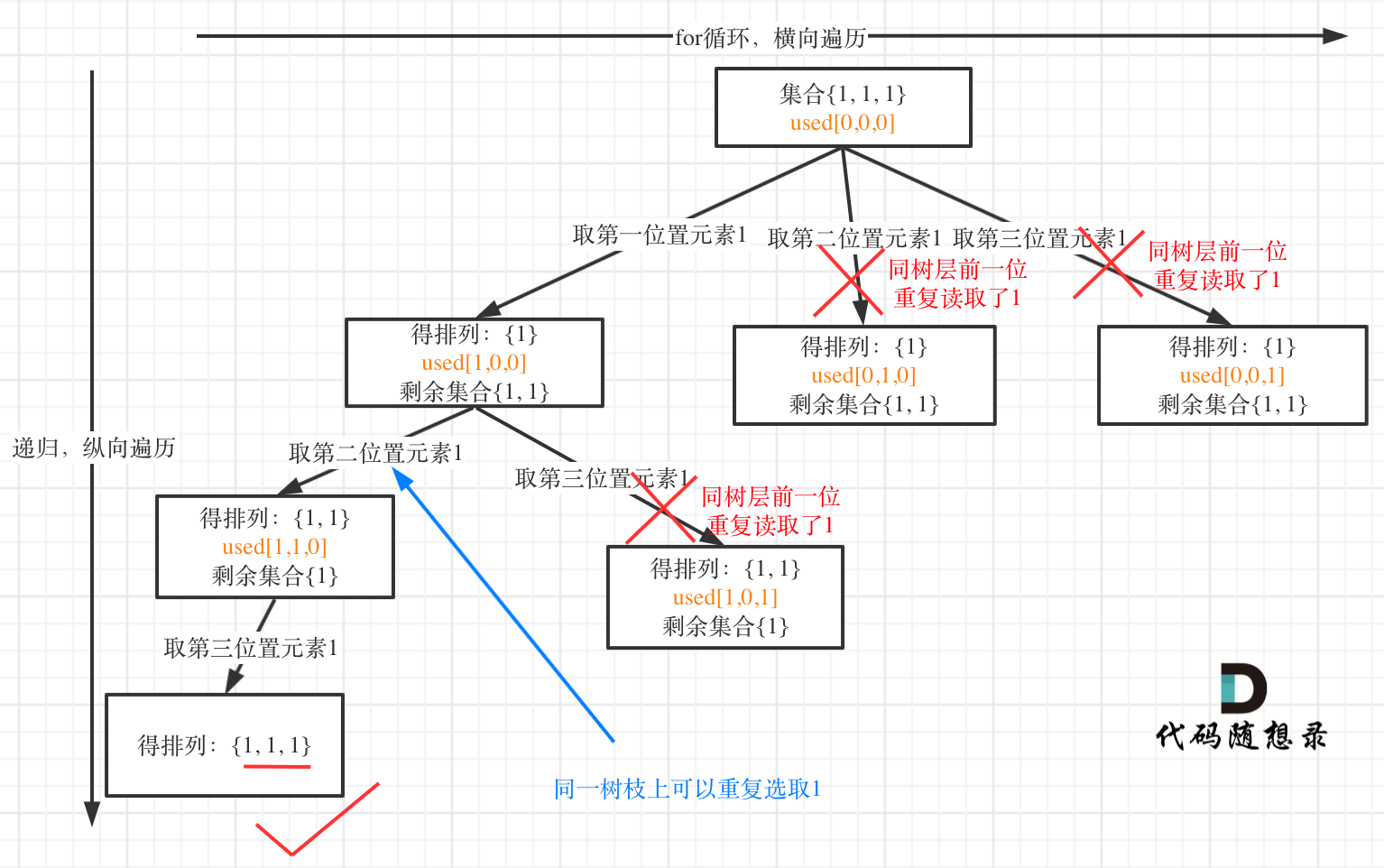
第一个是对树层进行去重，而第二个代码是对树枝去重。

对于排列问题，树层去重 与 树枝去重 都是可行，区别在于 树层的效率会比较高一点。

详细差别如图：

树层去重

 

树枝去重