代码随想录算法Day23 | 669. 修剪二叉搜索树 ，108.将有序数组转换为二叉搜索树 ， 538.把二叉搜索树转换为累加树 ， 总结篇

669. 修剪二叉搜索树

题目链接：669. 修剪二叉搜索树 - 力扣（LeetCode）

思路

在 删除二叉搜索树中节点值为key的节点 这一题中，分五种情况来考虑，找到节点后删除即可。

而这道题是要求删除所有不在[low, high]之间的节点。

最简单的方法，遍历所有节点，如果不在low, high]范围，返回null。

但这种方法存在一定问题。

按照这种方法，会直接删除以该节点为根的树，如果这个树中此时还存在符合low, high]范围的节点的话，也会 被删除。如图所示。

 

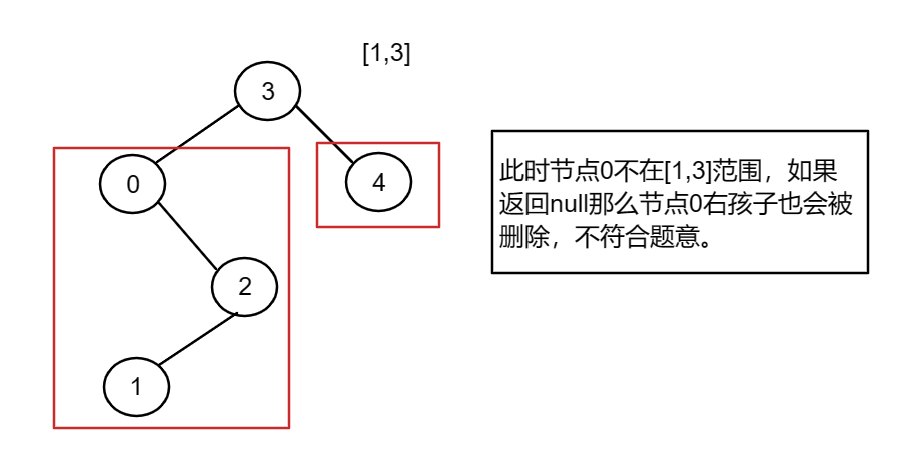
所以该方法不可行，但在上图中我们发现节点0并不符合区间要求，那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了（就是把节点0从二叉树中移除）。

因此我们可以得到单层递归的逻辑。

• 如果root（当前节点）的元素小于low的数值，那么应该递归右子树(二叉搜索树特性，右子树的节点大于当前节点)，并返回右子树符合条件的头结点。
• 如果root(当前节点)的元素大于high的，那么应该递归左子树(二叉搜索树特性，左子树的节点小于当前节点)，并返回左子树符合条件的头结点。
• 接下来要将下一层处理完左子树的结果赋给root->left，处理完右子树的结果赋给root->right。

 

 

代码

递归法

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        if (root.val < low) {
            return trimBST(root.right, low, high);
        }
        if (root.val > high) {
            return trimBST(root.left, low, high);
        }
        // root在[low,high]范围内
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

迭代法

因为二叉搜索树的有序性，不需要使用栈模拟递归的过程。

在剪枝的时候，可以分为三步：

• 将root移动到[L, R] 范围内，注意是左闭右闭区间
• 剪枝左子树
• 剪枝右子树

代码如下：

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null){
            return null;
        }
        // 处理头结点不在[low,high]范围内的情况,让 root 移动到[low,high]范围内
        while (root != null && (root.val < low || root.val > high)){
            // 进入循环的root的值只有两种情况, 小于 low 或者 大于 high
            if (root.val < low) {
                root = root.right; // 小于low,根据搜索树特性,往右走。
            } else {
                root = root.left;// 大于high，往左走。
            }
        }

        TreeNode cur = root;
        // 处理 root 左孩子元素小于low的情况
        while (cur != null){
            while (cur.left != null && cur.left.val < low) {
                cur.left = cur.left.right;
            }
            cur = cur.left;
        }

        cur = root;
        // 处理 root 右孩子小于high的情况
        while (cur != null){
            while (cur.right != null && cur.right.val > high) {
                cur.right = cur.right.left;
            }
            cur = cur.right;
        }

        return root;
    }
}

108.将有序数组转换为二叉搜索树

题目链接：108. 将有序数组转换为二叉搜索树 - 力扣（LeetCode）

思路

这道题本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间。

分割点就是数组中间位置的节点。（当数组长度为偶数时，中间元素有两个，不同的选择也对应两种不同答案）

代码

// 递归: 左闭右开 [left,right)
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedArrayToBST(nums, 0, nums.length);
    }
    
    public TreeNode sortedArrayToBST(int[] nums, int left, int right) {
        if (left >= right) {
            return null;
        }
        if (right - left == 1) {
            return new TreeNode(nums[left]);
        }
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = sortedArrayToBST(nums, left, mid);
        root.right = sortedArrayToBST(nums, mid + 1, right);
        return root;
    }
}

// 递归: 左闭右闭 [left,right]
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        TreeNode root = traversal(nums, 0, nums.length - 1);
        return root;
    }

    // 左闭右闭区间[left, right]
    private TreeNode traversal(int[] nums, int left, int right) {
        if (left > right) return null;

        int mid = left + ((right - left) >> 1);
        TreeNode root = new TreeNode(nums[mid]);
        root.left = traversal(nums, left, mid - 1);
        root.right = traversal(nums, mid + 1, right);
        return root;
    }
}

// 迭代: 左闭右闭 [left,right]
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        if (nums.length == 0) return null;

        //根节点初始化
        TreeNode root = new TreeNode(-1);
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        Queue<Integer> leftQueue = new LinkedList<>();
        Queue<Integer> rightQueue = new LinkedList<>();

        // 根节点入队列
        nodeQueue.offer(root);
        // 0为左区间下标初始位置
        leftQueue.offer(0);
        // nums.size() - 1为右区间下标初始位置
        rightQueue.offer(nums.length - 1);

        while (!nodeQueue.isEmpty()) {
            TreeNode currNode = nodeQueue.poll();
            int left = leftQueue.poll();
            int right = rightQueue.poll();
            int mid = left + ((right - left) >> 1);

            // 将mid对应的元素给中间节点
            currNode.val = nums[mid];

            // 处理左区间
            if (left <= mid - 1) {
                currNode.left = new TreeNode(-1);
                nodeQueue.offer(currNode.left);
                leftQueue.offer(left);
                rightQueue.offer(mid - 1);
            }

            // 处理右区间
            if (right >= mid + 1) {
                currNode.right = new TreeNode(-1);
                nodeQueue.offer(currNode.right);
                leftQueue.offer(mid + 1);
                rightQueue.offer(right);
            }
        }
        return root;
    }
}

538.把二叉搜索树转换为累加树

题目链接：538. 把二叉搜索树转换为累加树 - 力扣（LeetCode）

思路

这道题可以理解成一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]。从后往前挨个累加即可。

那么我们就可以知道如何遍历这个二叉树，从树中可以看出累加的顺序是右中左，所以我们需要反中序遍历这个二叉树，然后顺序累加就可以了。

代码

递归法

class Solution {
    int sum;
    public TreeNode convertBST(TreeNode root) {
        sum = 0;
        convertBST1(root);
        return root;
    }

    // 按右中左顺序遍历，累加即可
    public void convertBST1(TreeNode root) {
        if (root == null) {
            return;
        }
        convertBST1(root.right);
        sum += root.val;
        root.val = sum;
        convertBST1(root.left);
    }
}

迭代法

class Solution {
    public TreeNode convertBST(TreeNode root) {
        if (root == null){
            return null;
        }
        // 记录前一个节点的数值
        int pre = 0;
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
            if (cur != null){
                stack.push(cur);
                cur = cur.right; // 右
            } else {
                cur = stack.pop(); // 中
                cur.val += pre;
                pre = cur.val;
                cur = cur.left; // 左
            }
        }
        return root;
    }
}