LeetCode--数组专题（1----33, 分开写，不然太长了）

一、数组简介：

　　数组是存储同一种数据类型（可以是基本数据类型，也可以是引用数据类型）多个元素的集合；

　　数据类型补充：

       

　　特点：1. 线性的结构；

　　　　　2. 数组一旦创建其长度是不可变的；

　　　　　3.  数组是引用数据类型；

　　分类：一维、二维、三维、多维（二维及以上就是俄罗斯套娃下有实例）；

　　声明方式：

        // 部分基本类型
        int[] ints = {1, 2, 3, 4};
        double[] doubles = {1.0, 2.0, 3.0};
        
        // 部分引用数据类型
        String[] strings = {"my", "name", "is", "peanut"};
        Object object1 = new Object();
        Object object2 = new Object();
        Object object3 = new Object();
        
        Object[] objects = {object1, object2, object3};

 

二、LeetCode Array Problems：

       number：001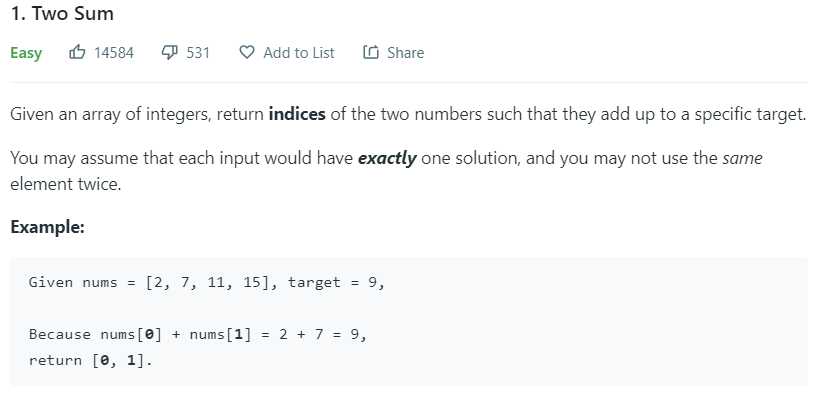

　　解析：题目的意思简单要是数组里面有任意两个元素的和等于目标元素 (target)，就返回两个数组元素下标；

　　　　　选用注意，要声明如果找不到，抛出错误信息提示；

class Solution {
    public int[] twoSum(int[] nums, int target) {
        // 用 HashMap 来装下找到数组元素及其下标
        Map<Integer, Integer> map = new HashMap<>();
        
        // 遍历数组，将key-->nums[i], value-->i, 装进HashMap中
        // 其实不用全部装，可以将循环体内代码放到下一个for-loop中
        // for (int i = 0; i < nums.length; i++) {
        //     map.put(nums[i], i);
        // }
        
        // 检验是否有符合条件的元素，有就返回
        for (int i = 0; i < nums.length; i++) {
            int result = target - nums[i];
            map.put(nums[i], i);
            // 要保证重复返回用一个下标的情形，例如 4+4=8，返回两次元素4的下标
            if (map.containsKey(result) && map.get(result) != i) {
                return new int[] {i, map.get(result)};
            } 
        }
        // 如果找不到返回错误
        throw new IllegalArgumentException("No two sum solution");
    }
}

=====================================================================

number：004

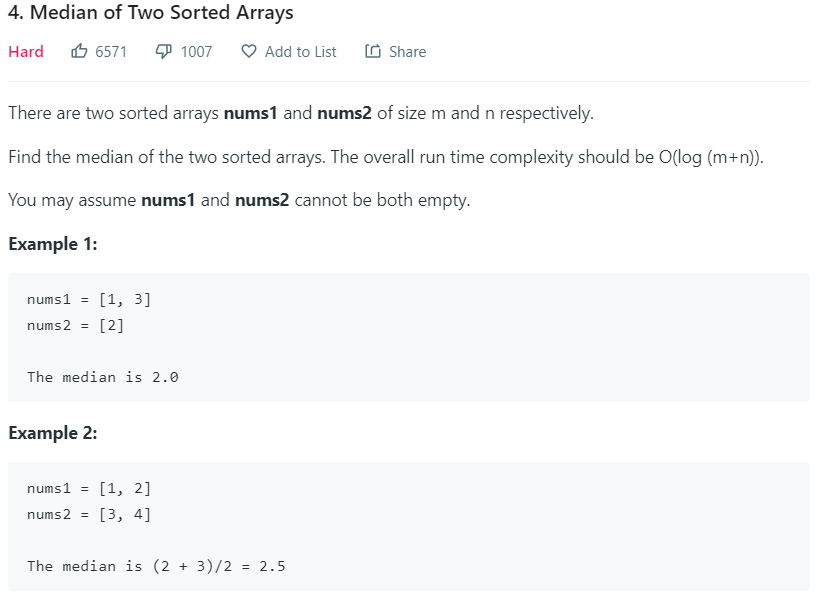
解析思路：https://www.bilibili.com/video/BV1B4411V7tP?from=search&seid=4209045980180096549 （大佬解析的很好）

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        
        // 有上面的思路可知，将长度小的数组放到前面，会快一点找到目标元素
        if (m > n) {
            int[] temp = nums1;
            nums1 = nums2;
            nums2 = temp;
            
            int tmp = m;
            m = n;
            n = tmp;
        }
        
        int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2;
        while (iMin <= iMax) {
            // 确定划分的长度
            int i = (iMin + iMax) / 2;
            int j = halfLen - i;
            if (i < iMax && nums2[j - 1] > nums1[i]) {
                 // i小了，将目标值往后面寻找
                iMin = i + 1;
            } else if (i > iMin &&  nums1[i-1] > nums2[j]) {
                 // i大了，将目标值往前面寻找
                iMax = i - 1;
            } else {
                // 找到了合适i，需要知道的是，当i在移动时，j同样在移动，
                int maxLeft = 0;
                if (i == 0) {
                    // 极端情况：数组1元素移动到开头后，此时 j=halfLen，则返回nums2[j-1]
                    maxLeft = nums2[j-1];
                } else if (j == 0) {
                    // 极端情况:i一直往右移，当j=0时，需要达成的条件为i=halfLen,
                    // 此时需要明白，需要两个数组的长度一样才能达到上述条件，
                    // 此时说明数组1中的元素均小于数组2的任意元素
                    maxLeft = nums1[i-1];
                } else {
                    // 在数组1和数组2之间选择一个作为左边最大
                    maxLeft = Math.max(nums2[j-1], nums1[i-1]);
                }
                // 校验元素的个数是不是奇数
                if ((m+n) % 2 == 1) {
                    return maxLeft;
                }
                
                int minRight = 0;
                if (i == m) {
                    // 极端情况：数组1元素移到了最右边，说明需要选定的右半部分的最小值为nums2[j]
                    minRight = nums2[j];
                } else if (j == n) {
                    // 极端情况：因为长度小的数组放在前面，若是j=n，则说明n-m <= 1,
                    // 此外，需要数组1的任意元素都要大于数组2的元素
                    minRight = nums1[i];
                } else {
                    // 在数组1和数组2之间选择一个作为右边最小
                    minRight = Math.min(nums2[j], nums1[i]);
                }
                return (maxLeft + minRight) / 2.0;
            }
        }
        return 0.0;
    }
}

============================================================================

11. Container With Most Water    难度：Medium

解析思路：题目意思找出两条线，与x轴一起构成一个容器，使容器中的水最多。

　　　　第一种思路就是双层for循环找出最大的容器，时间复杂度为O(n^2);

　　　　第二种思路是由两头向中间移动，每次要么移左边，要么移右边，选出最大的，时间复杂度为O(n).

　　　　

class Solution {
    public int maxArea(int[] height) {
        
//         int maxArea = 0;
//         for (int i = 0; i < height.length; i++) {
//             for (int j=i+1; j < height.length; j++) {
                   保留每次容器比较的最大值
//                 maxArea = Math.max(maxArea, Math.min(height[i], height[j]) * (j - i));
//             }
//         }
        
//         return maxArea;
        
        
        // 定义左右两边，以及最大值
        int left = 0, right = height.length - 1;
        int maxArea = 0;
        while (left < right) {
            // 保留每次容器比较的最大值
            maxArea = Math.max(maxArea, Math.min(height[left], height[right]) * (right - left));
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return maxArea;
    }
}

=======================================================================================

15. 3Sum  难度：Medium

解析思路：手写，将就看吧

/**
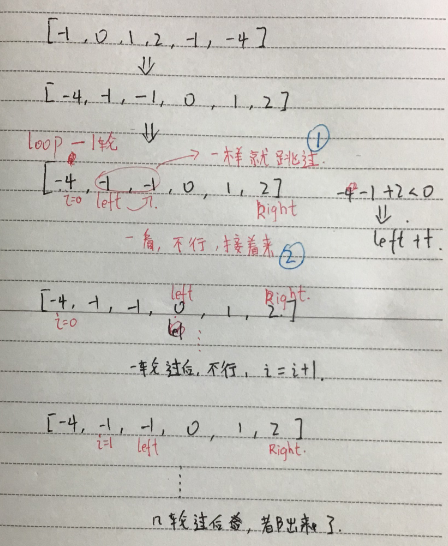
 * 其实此题正好衔接上面一题的思路，由两边向中间，
 * 不同的是需要确定一个元素作为基点；
 * 算法的时间复杂度为：O(n * n)，最坏情况,第一个n是基点的for循环，第二个是个前一题一样
 */
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        // 创建接受结果的列表
        List<List<Integer>> result = new ArrayList<>();
        
        // 校验元素长度
        if (nums.length < 3) {
            return result;
        }
        // 先排序，有序数组更好操作，这一思想很重要
        Arrays.sort(nums);
        for (int i = 0; i < nums.length-2; i++) { // 基点的 for-loop
            if (i > 0 && nums[i] == nums[i - 1]) { //碰到一样的就接着跳
                continue;
            }
            
            // 其实这边可以拓展为三元素这和不仅仅为 0 的状况
            int target = -nums[i];
            // 定义左边元素，右边元素，寻找两元素之和==target
            int left = i + 1;
            int right = nums.length - 1;
            while (left < right) {
                int sum = nums[left] + nums[right];
            
                if (sum  == target) {  // 找到答案
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    // 和上面一样， 遇到一样的就跳过
                    while (left < right && nums[left] == nums[left+1]) {
                        left++;
                    }
                    while (left < right && nums[right] == nums[right-1]) {
                        right--;
                    }
                    // 因为答案已找到，而且同样元素也已跳过，这里直接left，right两边齐头并进
                    left++;
                    right--;
                } else if(sum < target) {  // 按情况，左元素或者右元素移动
                    left++;
                } else {
                    right--;
                }
            }
        }
        return result;  // 返回答案
    }
}

==========================================================================

16. 3Sum Closest   难度：Medium

解析思路：参照上面吧，都差不多。。。

/**
 * 三元素求和的衍生题，但记住是离答案最近的选择，
 * 所以说，绝对值不能忘
 */
class Solution {
    public int threeSumClosest(int[] nums, int target) {
        int n = nums.length;
        // 排序对于数组的求和算法题很重要
        Arrays.sort(nums);  
        int result = nums[0] + nums[1] + nums[2];
        for (int i = 0; i < n-2; i++) {
            // 和前两题类似的场景
            int left = i + 1;
            int right = n - 1;
            while (left < right) {
                int sum = nums[i] +nums[left] +nums[right];
                // 记得加上绝对值
                if (Math.abs(sum-target) < Math.abs(result-target)) {
                    result = sum;   // 把小的存在result
                }
                if (sum == target) {
                    return target;  //如果等于，直接返回
                } else if (sum < target) { 
                    left++;
                } else {
                    right--;
                }
            }
        }
        return result;
    }
}

 =========================================================================

18. 4Sum    难度：Medium

 

 

解析思路：

 

/**
 * 经典的4元素求和问题，和前面的3元素求和不一样的是：需要定两个基点，
 * 一个基点开始定在最左边，一个基点在最右边，然后向中间压缩
 * 时间复杂度O(n^2)
 */
class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        
        // **数组排序
        Arrays.sort(nums);
        // 如实数组长度为零，直接返回
        if (nums.length == 0) {
            return list;
        }
        // 如果数组最小值*4 大于 target，或者数组最大值*4 小于target，直接返回
        if (4 * nums[0] > target || 4 * nums[nums.length-1] < target) {
            return list;
        }
        // 定义左基点，他需要留下三个空位置，left，right，end（右基点）
        for (int start = 0; start < nums.length -2; start++) {
            if (start-1 >= 0 && nums[start-1] == nums[start]) { // 遇到一样的就跳过
                continue;
            }
             // 定义右基点end，他需要留下三个空位置，start，left，right
            for (int end = nums.length-1; end > start+2; end--) {
                if (end+1 < nums.length-1 && nums[end+1] == nums[end]) { // 遇到一样的就跳过
                    continue;
                }
                
                if (4 * nums[start] > target || 4 * nums[end] < target) { // 如果数组最小值*4 大于 target，或者数组最大值*4 小于target，直接返回
                    break;
                }
                int left = start+1;
                int right = end-1;
                // 将收尾两端放在一起，类似于前面三元素和的单个基点
                int fixedSum = nums[start] + nums[end];
                int remSum = target - fixedSum;
                
                while (left < right) {
                    if (2 * nums[left] > remSum || 2*nums[right] < remSum) {  // 如果数组最小值*4 大于 target，或者数组最大值*4 小于target，直接返回
                        break;
                    }
                    
                    int sum = nums[start] + nums[left] + nums[right] + nums[end];
                    if (sum == target) {  // 终于找到你，于是去领证了
                        list.add(Arrays.asList(nums[start], nums[left], nums[right], nums[end]));
                    
                    
                        while (left+1 < right && nums[left+1] == nums[left]) { // 跳过一样的
                            left++;
                        }
                        while (left < right-1 && nums[right-1] == nums[right]){  // 跳过一样的
                            right--;
                        }
                        left++;
                        right--;
                    } else if (sum > target) { // 元素和大了，往左移
                        right--;
                    } else {    // 元素和小了，往右移
                        left++;
                    }
                }
            }
        }
        return list;
    }
}

=========================================================================

26. Remove Duplicates from Sorted Array    难度：Easy

 

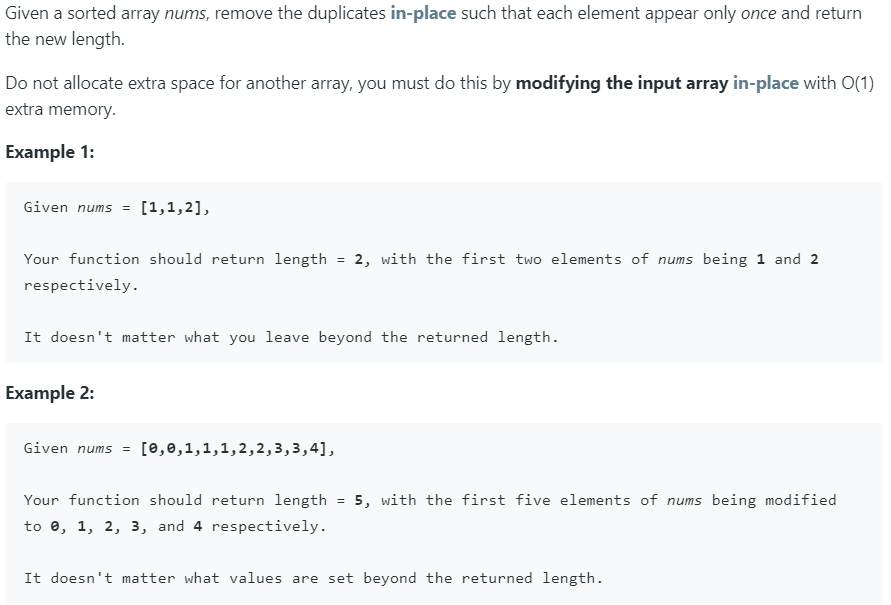
解析思路：

 

/**
 * 时间复杂度：O(n)
 */
class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums.length==0) {  // 校验数组长度
            return 0;
        }
        int i = 0;
        for (int j=1; j < nums.length; j++) {
            if (nums[j] != nums[i]) {
                // 一样的时候，j++，i不变，不一样时，后一个覆盖不一样的前一个，参照思路解析
                i++;
                nums[i] = nums[j];
            }
        }
        // 不用纠结数组会变成什么样，返回正确答案就行
        return i+1;
    }
}

==============================================================================

27. Remove Element   难度：Easy

解析思路参照前面一题的；

class Solution {
    public int removeElement(int[] nums, int val) {
        // 定义数组中含有与目标值不一样的元素个数
        int count = 0;
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            if (nums[i] != val) {  // 和上一题很像，一样时i++，count不变，不一样时将覆盖前面
                nums[count] = nums[i];
                count++;
            }
        }
        // 和上一题一样，不要在意数组变成什么样，打哪正确就好
        return count;
    }
}

 

===============================================================================

31. Next Permutation   难度：Medium

解析思路：题目比较有意思，说的是下一个数组刚好比前一个数组大一点点，例如：1， 2， 3， 4--->1, 2, 4, 3, 在下面就是1， 3， 2， 4.......当然答案是第一个，后面只是演示

/**
 * 时间复杂度：O(n)
 */
class Solution {
    public void nextPermutation(int[] nums) {
        // 从最后的两个数入手，所以 i=nums.length-2;
        int i = nums.length-2;
        while (i >= 0 && nums[i+1] <= nums[i]) {
            // 如果最后一个数大于前一个数，跳过，放在后面交换，不然i--，再往前找一位
            i--;
        }
        if (i >= 0) {
            int j = nums.length -1;
            // 若是上面的i没有减：下面这一步的作用主要是看倒数第三个能不能和倒数第一个位置的元素交换
            // 若是上面的i减了：下面这一步的作用主要是看倒数第二个能不能和倒数第三个位置的元素交换
            while (j >= 0 && nums[j] <= nums[i]) {
            //如果最后一个数小于前一个数，j--，交换两者位置
                j--;
            }
            swap(nums, i, j);
        }
        /**
         * 如果最后两个交换不了，就往前推一位，若可以，将倒数第2位和倒数第3位交换，
         * 然后将观察现在的倒数第2位和倒数第一位是否需要交换
         */
        reverse(nums, i+1);
    }
    
    /**
     * 交换过后，检查后面元素是否可以再次交换，保证符合题意
     */
    private void reverse(int[] nums, int start) {
        int i = start, j = nums.length-1;
        while (i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
    }
    
    /**
     * 元素交换函数
     */
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

==============================================================================================

 33. Search in Rotated Sorted Array   难度：Medium

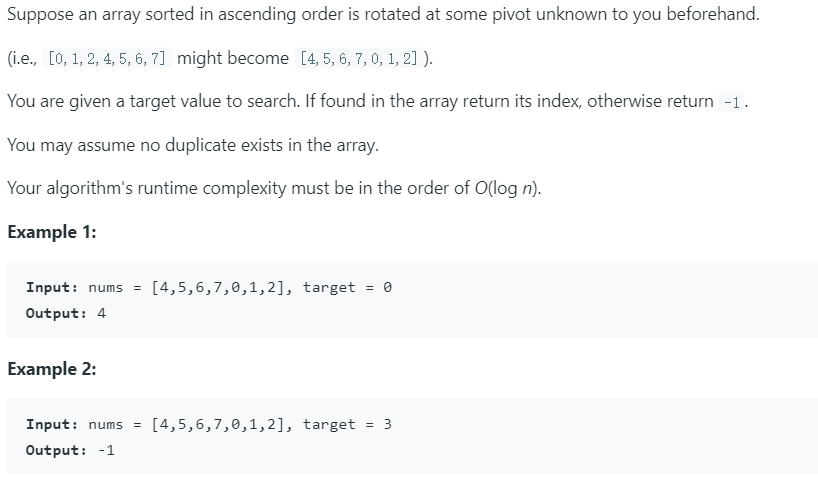
解析思路：根据不同情况可分开使用二分查找

         int start = 0;
         int end = nums.length-1;
         
         while(start<=end){
             
             int mid = start+(end-start)/2;

             if(nums[mid] == target)
                 return mid;
             
             // Check ont the left Side
             if(nums[start] <= nums[mid]){
                 if(target >= nums[start] && target <= nums[mid])
                     end = mid-1;
                 else
                     start =mid+1;
             }
             // Check ont the Right Side
             else if(nums[mid] <= nums[end]){
                 if(target>=nums[mid] && target<= nums[end])
                     start = mid+1;
                 else
                     end =mid-1;
             }
                  
         }
         return -1;