[笔记]Tarjan算法求强联通分量（SCC）学习笔记

[笔记]Tarjan算法求强联通分量（SCC）学习笔记

P1 定义

1. dfs搜索树：就是在搜索过程中，所构成的树状结构，并且几个节点的搜索树中不包括他的父亲。

2. 树边、横叉边、返祖边、前向边：以下图举例子：

   

   其中树边就是dfs搜索树所走的边（例如黑色的 \(1\to 2\) ，即以搜索的节点走向未搜索的节点的边）；横叉边是在搜索时遇到了已经访问过的节点，但是这个节点并不是该节点的祖先（例如蓝色的 \(7\to 9\)），这时走的边；返祖边是一个点在搜索时走到自己的祖先的那条边（例如红色 \(7\to1\)）；前向边是一个节点访问子树的节点所走的非树边（例如绿色\(3\to6\)）。

   这里写一些结论。

   除了树边，通过其它的边所访问的节点都是已经走过、标记的。以下是证明。

   对于返祖边显然，横叉边的定义就已经有这个条件了。对于前向边，如果节点不是被访问过的，那么这条前向边就会变成树边，那么就不符合定义了。

3. 强联通分量：指在一个有向子图中，任意两点都能到达。

   1. 结论：如果一个点在一个强联通分量中，是第一个在搜索中遇到的，那么这个强联通分量的其他节点必定在以该节点为根的搜索树中，这个点称为这个强联通分量的根。

      证明：设这个点为 \(u\) ，如果一个点 \(v\) 在这个强联通分量而不在这个搜索树中，那么必定有一条边离开了搜索树去到了 \(v\) ，而且这样的边只可能是横叉边或者返祖边（绝不可能是树边），并且 \(v\) 也可以回到搜索树中。那么显然这个点已经被访问过，它在dfs中可以反向搜索到 \(u\)，\(u\) 就不是第一个遇到的，与假设相反。

   2. 结论：一个点必定属于一个强联通分量。

P2 Tarjan算法

P2.1 low和dfn的定义

\(\text{dfn}[i]\) 表示一个点在dfs中是第几个被搜到的。

这里用 \(\text{subtree}[i]\) 表示以 \(i\) 为根的搜索树，\(\text{low}[i]\) 表示以下节点的最小值：\(\text{dfn}[i]\)、\(\min_{u\in \text{subtree[i]}} \text{dfn}[u]\)、在 \(\text{subtree}[i]\) 中能用一条非树边走到的节点的 \(\text{dfn}\) 值。它相当是一个点在搜索树中，只走一条非树边能走到最早被访问过的节点。

P2.2算法流程

由于我们有P1中的第二个结论，所以只用知道那些点是一个强联通分量的根，就可以找出强联通分量了。

具体来说，我们可以用一个栈，记录哪些点在栈中。如果我们发现一个点，它如果是一个强联通分量的根，就可以知道它和在栈中在它上面的点，构成一个强联通分量。

我们来考虑一下这个为什么是对的。首先有一个事实，一个点在栈中上面的点肯定会在它的搜索树中。然后我们考虑一下一个搜索深度较深的强联通分量，会不会影响一个深度较浅的强联通分量。答案是否定的，因为在回溯前，就把那些点弹出栈中。就不会再被计算进深度较浅的强联通分量。

然后现在的问题就是这么判断这个点到底是不是强联通分量的根。首先，判定条件是 \(\text{dfn}[x]\) 是否等于 \(\text{low}[x]\)，如果是，那么就是强联通分量的根。来说一下 \(\text{dfn,low}\) 的计算。设我们现在在计算\(\text{dfn}[x],\text{low}[x]\)，有一个与它相邻的节点 \(y\) （\(y\) 肯定不是他的父亲），分类讨论：

1. \(y\) 没有被访问过：对 \(y\) 进行搜索，然后 \(\text{low}[x]=\min\{\text{low}[x],\text{low}[y]\}\)。显然 \(y\) 只走一条非树边得到的 \(\text{low}\) 值，\(x\) 也可以走一条树边到 \(y\) 之后也只走一条非树边到达。
2. \(y\) 被访问过且在栈中：根据 \(\text{low}\) 定义，\(\text{low}[x]=\min\{\text{low}[x],\text{dfn}[y]\}\)。
3. \(y\) 被访问过且不在栈中：那么 \(y\) 属于另外一个强联通分量，不能影响这个强联通分量，所以不做处理。

现在在说一下第三个的必要性。

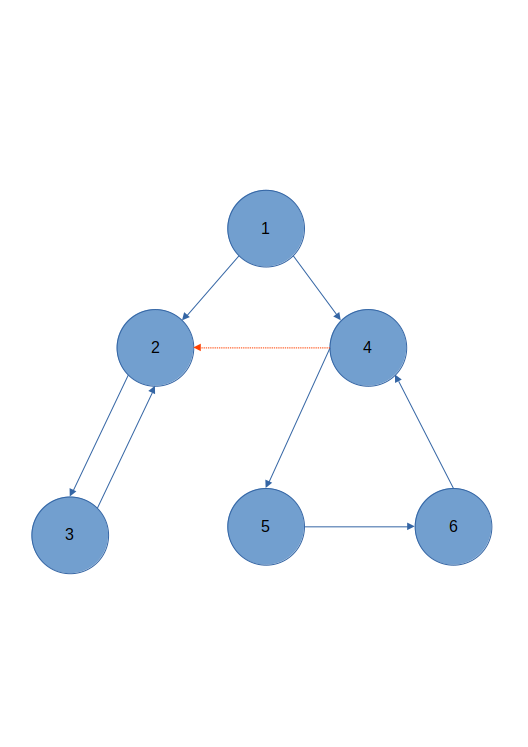
节点中黑色数字代表节点的 \(\text{dfn}\) 值，那么红色即为一条横叉边。注意这里的搜索是节点4搜完了节点5、6，通过红色边搜到了节点2。如果我们不把第三个考虑，就会出现 \(\text{low}[4]=2\) 的情况，那么就会出现节点 4、5、6 不构成一个强联通分量，显然是不对的。如果加了这条限制，那么 \(\text{low}[4]=\text{dfn}[4]=4\)，就是正确的。用一句话来概括就是：计算当前的强联通分量时，不能被之前计算过的强联通分量所影响了。

我们来思考一下这个判断是否为强联通分量的判断方法为什么是对的。首先有一个结论：在一个子树 \(\text{subtree}_x\) 中，必定有 \(\forall i \in \text{subtree}_x,\text{low}[i]\ge\text{low}[x],\text{dfn}[i]\ge\text{dfn}[i]\)。假设一个节点 \(u\) ，满足这个条件，可以断定这个点没有连接返祖边，而且横叉边、前向边对它没有影响。这个点和它子树中的一些节点，就能构成强联通分量，而且它是第一个被访问的，因为它只经过一条非树边能到达最早的节点就是他自己。这符合强联通分量的定义。

P3 缩点

学SCC的价值之一就是对一个有向图进行缩点，把图变成DAG。具体来说，在同一个强联通分量的点变成一个点，然后那些边的连接关系不变。

P4 代码

void Tarjan(int x,int fa)
{
    dfn[x]=low[x]=++num,sta[++top]=x;
	for(int i=hd[x];i;i=nxt[i])
    {
        if(to[i]!=fa)
        {
            if(!vis[to[i]])
                dfs(to[i],x),low[x]=min(low[x],low[to[i]]);
            else if(insta[to[i]])
                low[x]=min(low[x],dfn[to[i]]);
		}
	}
    if(low[x]==dfn[x])
    {
        sccnum++;
        while(sta[top]!=x)	scc[sccnum].push_back(sta[top]),insta[sta[top]]=0,top--;
        scc[sccnum].push_back(sta[top]),insta[sta[top]]=0,top--;
	}
}