[笔记]浅谈分块

[笔记]浅谈分块

0 前言

分块真的是一个很好的思想和数据结构。它是一种优雅的暴力。

——LYM

1 分块入门

一般来说，分块解决的是在序列上的操作问题。在某种情况下，它可以运用一些简单的操作来解决一些线段树\树状数组\树套树较为恶心的题目。

用一道例题来引入吧。

数列分块入门 4

就是要设计一个支持区间加、区间求和查询的题目。

考虑（线段树）分块。

先来想想最暴力的做法，查询、修改都是 \(O(n)\) 。整体是 \(O(nm)\) 。显然会炸。

不妨先把序列分成 \(\sqrt n\) 块（实际上会多一点或少一点，但这不影响），每个块的长度为 \(\sqrt {n}\)。

\[\underbrace{a_1,a_2,\cdots,a_{\sqrt{n}}}_{\text{第1个块}},\underbrace{a_{\sqrt{n}+1},a_{\sqrt{n}+2},\cdots,a_{2\cdot \sqrt{n}}}_{\text{第2个块}},\cdots,\underbrace{a_{(\sqrt{n}-1) \cdot \sqrt{n}+1},a_{(\sqrt{n}-1) \cdot \sqrt{n}+2},\cdots,a_{n}}_{\text{第} \sqrt{n} \text{个块}} \]

最后一个块的长度可能不是 \(\sqrt{n}\) ，块的个数也有可能会变动，但先不管。

设 \(b_1,b_2,\cdots,b_{\sqrt{n}}\) 为每一个块要统一加上的数；\(s_1,s_2,\cdots,s_{\sqrt{n}}\) 为每个块的实际的和 。

首先考虑修改。修改分为一下几个部分： 开头那段不完整的块，中间几段完整的块，最后那段不完整的块。

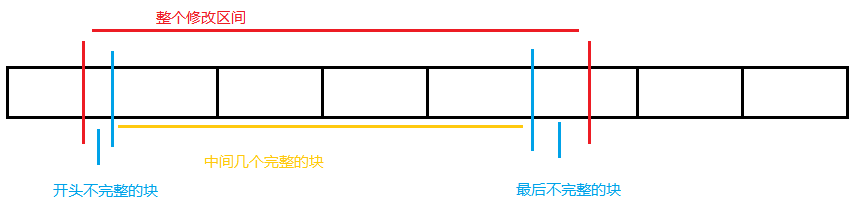
• 对于开头和后面不完整的块，我们直接暴力修改 \(a\) 与 \(s\) 数组。
• 对于中间几个完整的块，我们直接给每个块的 \(b_i\) 加上一个数。

那么，这样修改，一个数的真实值就是 \(a_i+b_{\text{id}(i)}\) ,其中 \(\text{id}(i)\) ，代表 \(i\) 在哪个块。

再来考虑询问操作。询问也分为三部分：开头那段不完整的块，中间几段完整的块，最后那段不完整的块。

• 对于完整的块，我们直接加上 \(s_i\)。
• 对于不完整的块中的元素 \(i\)，我们暴力加上 \(a_i+b_{\text{id}(i)}\) 。

查询和修改可能在同一个块中，我们特判一下，然后暴力修改/查询。

于是分块就完成了！

code

2 分块进阶

还是以一道题引入。

教主的魔法

对于这道题，我们依旧考虑分块。由于无序的序列再找数的时候很不方便，我们不妨把每个块都排序。这样在询问操作的时候，对于完整的块，显然可以二分；对于不完整的块，我们依旧暴力查找。

现在再来考虑修改操作。由于排完序之后的值的顺序是与原数组不一样的，但是修改又要是在原来的顺序进行修改的。所以，我们还是要保留原数组，并且还要一个记录对于单个块来说，它自己要加上独立的值。

具体的，如果是对于不完整的块，我们暴力修改，然后把这个块重新排序；对于完整的块，块内元素的相对大小不变，也就是说，它们的排完序后的顺序不变，我们就没必要再次排序了。在查询时，再统一加上块内要统一加的值。这个对于完整的块的修改操作，类似于线段树的懒惰标记。

查询与修改在同一个块之中的操作，同上。

code

SDOI2008 郁闷的小 J

不知道你们在做这道题的感受如何，反正我是挺郁闷的。当时改了一个下午+一个晚上，倒不是分块有多难打，而是我错在输入问题上！！！在这里，我必须提两句：以后输入字符都要用scanf("%s",...) ，而不是 scanf("%c",...) 。我因为这个，RE+TLE，改的真的很久。

---

好了废话不多说，让我们开始分块（虽然这是个带修莫队板子）。

显然对于编号，需要离散化。在这里介绍 gp_hash_table 这个东西，它满足了我们平常对于 map 的使用，但比 map 更快。然而它是 GNU 的，显然你要用GNU的编译器，但 NOI 似乎是开放了带下划线的东西。

我们每个块都来一个标记数组。那么，对于修改，显然 \(O(1)\) 暴力；对于查询，不完整的块依旧暴力，对于完整的块，显然直接 \(O(1)\) 访问。

code

3 分块的广泛运用

LYM之所以说分块是个好东西，必定有原因。比如像这道题，一个LCT的模板题，分块也能过！

HNOI2010 弹飞绵羊

你可能会问：怎么能用分块呢？

显然也是可以的，只是分块的思想似乎要改变一下了。我想这道题如果你能独立思考出来，就说明你对分块还算熟悉了，你可以把分块拓展到另外一些题目。所以在看下面的分析之前，希望你先思考5min。

---

我们不妨令 \(f(i),g(i)\) 分别表示：第 \(i\) 个点需要跳几次能跳出块，跳出块之后的位置在哪里。

那么就非常好做了，笔者觉得要给读者一些独立的思考空间。所以在这里，来探讨另外一个问题：如何快速求出 \(f(i),g(i)\) ？

显然你可以用记忆化搜索，但这里有一个 \(O(n)\) 的 dp 的方法。

先来分类讨论一下，一个点在跳出块时有两种情况：

1. 跳一次即可跳出块，即: \(i+k_i \ge\) 所属块的有节点。
2. 需要跳几次。

对于第一种情况，\(f(i)=1,g(i)=i+k_i\) ；对于第二种情况，我们假设 \(j=i+k_i\) ，也就是这个点跳一次后再块内的位置，假设已经求出 \(f(j),g(j)\)，显然 \(f(i)=f(j)+1,g(i)=g(j)\) 。

这是不是有点像转移方程？就是顺序有点奇怪，我们只要倒序转移就好了。

code

4 分块的时间复杂度

• 对于修改操作，一般对于完整的块是 \(O(1)\) ，不完整的块时 \(O(\sqrt{n})\)，至多有2个不完整的块，所以单次是 \(O(\sqrt{n})\)。
• 对于询问，和修改类似，一般是 \(O(\sqrt{n})\) 。

所以时间复杂度是 \(O(m\sqrt{n})\) 。还算快。

分块的时间复杂度取决于你对块的用法以及一些具体操作。

5 参考文献

• 分块思想 - OI Wiki

• 块状数组 - OI Wiki