排序算法

一、排序算法的分类

 

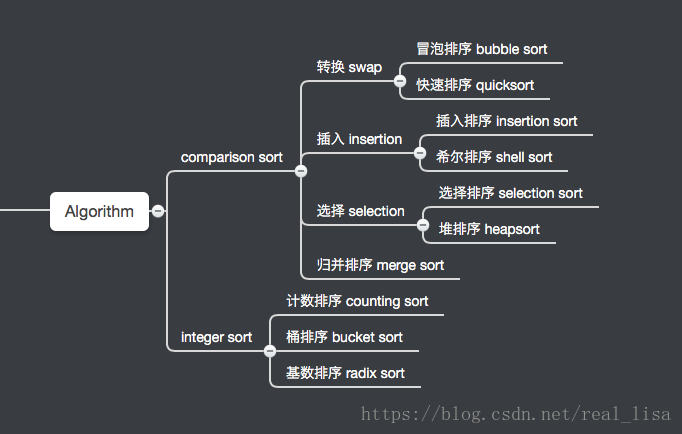
1. 比较排序 VS 非比较排序

是否需要比较两个元素的大小才能进行排序

2. 交换排序 VS 插入排序 VS 选择排序

交换：每次只调换两个元素之间的位置

插入：遍历到的元素放入之前维护的已完成排序的序列中

选择：选择剩余元素中最大或最小的元素

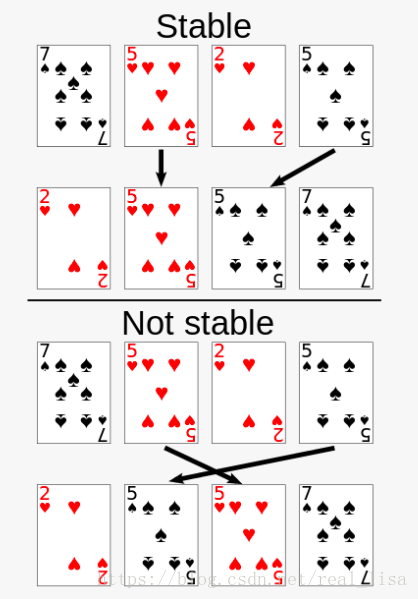
 3. 排序算法的稳定度

如果排序算法并不改变两个相同值的元素的相对位置，则此算法的稳定度高

 

 

 

二、冒泡排序

1.算法

每次遍历，从头至尾依次比较两两相邻元素是否满足排序条件，不满足则交换两者位置

当一次遍历中没有发生交换操作后，结束遍历

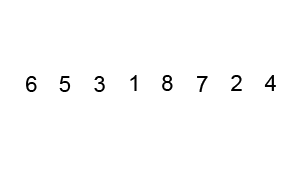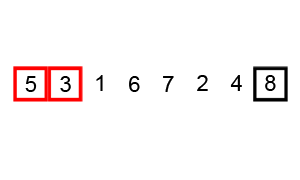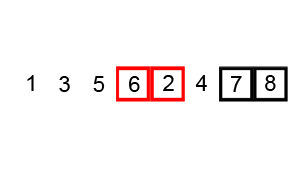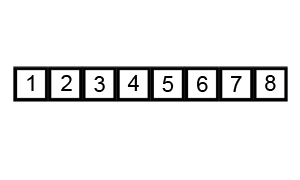
2.代码

C++：

void bubble(vector<int> &array) {
    if (array.size() == 0) {
        return;
    }
    bool flag = false;
    while (!flag) {
        flag = true;
        for (int i = 0; i < array.size() - 1; i++) {
            if (array[i] > array[i + 1]) {
                int temp = array[i];
                array[i] = array[i + 1];
                array[i + 1] = temp;
                flag = false;
            }
        }
    }
}

JAVA：

void bubble(int[] array) {
    if (array.length == 0) {
        return;
    }
    boolean flag = false;
    while (!flag) {
        flag = true;
        for (int i = 0; i < array.length - 1; i++) {
            if (array[i] > array[i + 1]) {
                int temp = array[i];
                array[i] = array[i + 1];
                array[i + 1] = temp;
                flag = false;
            }
        }
    }
}

Python：

def bubble(array):
    if not array:
        return
    flag = False
    while not flag:
        flag = True
        for i in range(0, len(array)-1):
            if array[i] > array[i+1]:
                array[i], array[i+1] = array[i+1], array[i]
                flag = False

3.优化

每次遍历后，最后一次交换操作之后的所有元素均已完成排序，下一次遍历的终点可以前提至最后交换操作元素的索引位置

4.评估

时间复杂度：O(n2)

空间复杂度：O(1)

稳定性：稳定

 

三、快速排序

1.算法

每次选择一个基数，将剩余元素划分为大于基数和小于基数的两组

在两组中分别重复上述过程，直到分组无需排序为止

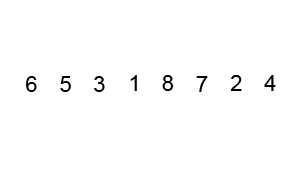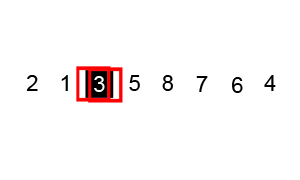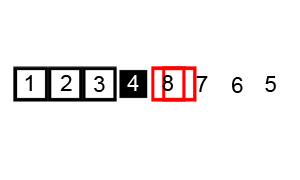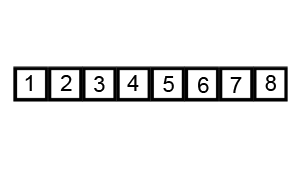
2.代码

C++：

void quick(vector<int> &array, int begin, int end) {
    if(begin>=end){
        return;
    }
    int pivot = array[begin];
    int i = begin + 1;
    int j = end;
    while(i <= j){
        while(i<=j && array[i]<=pivot){
            i++;
        }
        while(i<=j && array[j]>pivot){
            j--;
        }
        if(i<=j) {
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }
    array[begin] = array[j];
    array[j] = pivot;
    quick(array, begin, j-1);
    quick(array, j+1, end);
}

JAVA：

void quick(int[] array, int begin, int end) {
    if(begin>=end){
        return;
    }
    int pivot = array[begin];
    int i = begin + 1;
    int j = end;
    while(i <= j){
        while(i<=j && array[i]<=pivot){
            i++;
        }
        while(i<=j && array[j]>pivot){
            j--;
        }
        if(i<=j) {
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }
    array[begin] = array[j];
    array[j] = pivot;
    quick(array, begin, j-1);
    quick(array, j+1, end);
}

Python：

def quick(array, begin, end):
    if begin >= end:
        return
    pivot = array[begin]
    i = begin + 1
    j = end
    while i <= j:
        while i <= j and array[i] <= pivot:
            i += 1
        while i <= j and array[j] > pivot:
            j -= 1
        if i <= j:
            temp = array[i]
            array[i] = array[j]
            array[j] = temp
    array[begin] = array[j]
    array[j] = pivot
    quick(array, begin, j - 1)
    quick(array, j + 1, end)

3.优化

每次从头、尾及中间元素中，选择中位值作为基数

4.评估

时间复杂度：O(nlogn)

空间复杂度：O(longn)

稳定性：稳定

 

四、插入排序

1.算法

维护有序子列，每次从待排序子列中取出一个元素插入到有序子列的合适位置

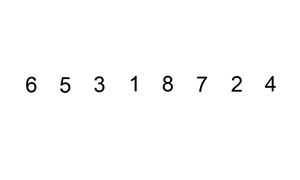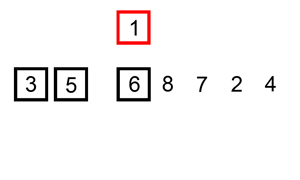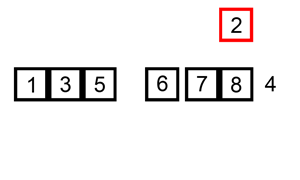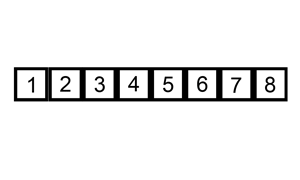
2.代码

C++：

void insert(vector<int> &array) {
    for(int i=1;i<array.size();i++){
        int j = i;
        int temp = array[j];
        while(j>0 && array[j-1]>temp){
            array[j] = array[j-1];
            j--;
        }
        array[j] = temp;
    }
}

JAVA：

void insert(int[] array) {
    for(int i=1;i<array.length;i++){
        int j = i;
        int temp = array[j];
        while(j>0 && array[j-1]>temp){
            array[j] = array[j-1];
            j--;
        }
        array[j] = temp;
    }
}

Python：

def insert(array):
    for i in range(1, len(array)):
        j = i
        temp = array[j]
        while j > 0 and array[j-1] > temp:
            array[j] = array[j-1]
            j -= 1
        array[j] = temp

3.优化

4.评估

时间复杂度：O(n2)

空间复杂度：O(1)

稳定性：稳定

 

五、希尔排序

1.算法

每次根据间距将序列划分为数个子列，分别在每个子列中进行插入排序

缩短间距大小，重复上述过程，直到间距为一

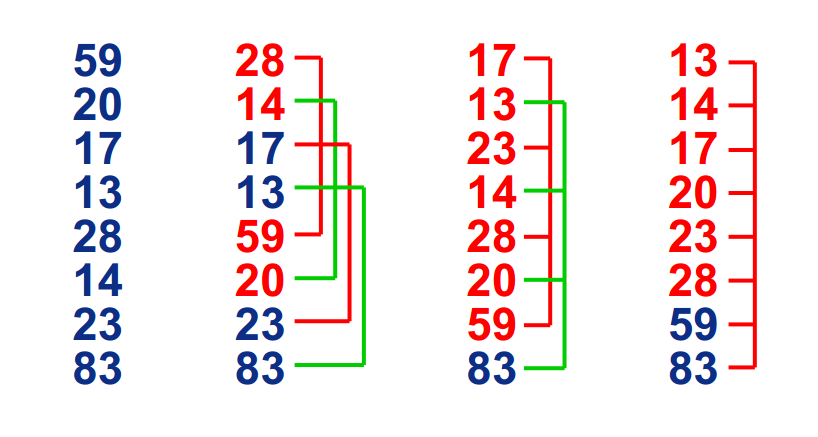
2.代码

C++：

void shell(vector<int> &array) {
    int length = array.size();
    for(int gap = length/2;gap>=1;gap/=2){
        for(int i=gap;i<length;i++){
            int j = i;
            int temp = array[j];
            while(j-gap>=0 && array[j-gap]>temp) {
                array[j] = array[j - gap];
                j -= gap;
                array[j] = temp;
            }
        }
    }
}

JAVA：

void shell(int[] array) {
    int length = array.length;
    for(int gap = length/2;gap>=1;gap/=2){
        for(int i=gap;i<length;i++){
            int j = i;
            int temp = array[j];
            while(j-gap>=0 && array[j-gap]>temp) {
                array[j] = array[j - gap];
                j -= gap;
                array[j] = temp;
            }
        }
    }
}

Python：

def shell(array):
    length = len(array)
    gap = int(length/2)
    while gap >= 1:
        for i in range(gap, length):
            j = i
            temp = array[j]
            while j-gap >= 0 and array[j-gap] > temp:
                array[j] = array[j-gap]
                j -= gap
            array[j] = temp
        gap = int(gap/2)

3.优化

4.评估

时间复杂度：O(n1.3)

空间复杂度：O(1)

稳定性：不稳定

 

六、选择排序

1.算法

维护有序子列，每次从待排序子列中取出最小元素插入到有序子列的末端

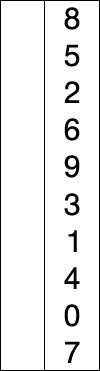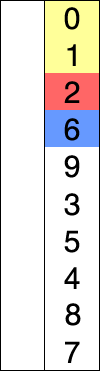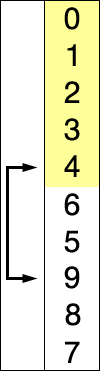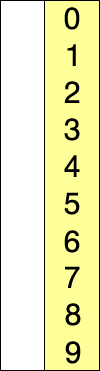
2.代码

C++：

void selection(vector<int> &array) {
    int length = array.size();
    for(int i=0;i<length;i++){
        int min = array[i];
        int index = i;
        for(int j=i+1;j<length;j++){
            if(array[j]<min){
                min = array[j];
                index = j;
            }
        }
        if(index!=i) {
            array[index] = array[i];
            array[i] = min;
        }
    }
}

JAVA：

void insert(int[] array) {
    for(int i=1;i<array.length;i++){
        int j = i;
        int temp = array[j];
        while(j>0 && array[j-1]>temp){
            array[j] = array[j-1];
            j--;
        }
        array[j] = temp;
    }
}

Python：

def selection(array):
    length = len(array)
    for i in range(0, length):
        minimal = array[i]
        index = i
        for j in range(i+1, length):
            if array[j] < minimal:
                minimal = array[j]
                index = j
        if index != i:
            array[index] = array[i]
            array[i] = minimal

3.优化

4.评估

时间复杂度：O(n2)

空间复杂度：O(1)

稳定性：稳定

 

七、归并排序

1.算法

将数组递归二分直到分解为数个单元素数组

再依次序按大小顺序将每对分解数组合并

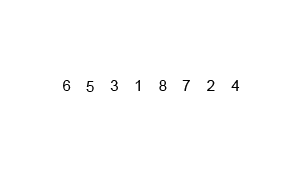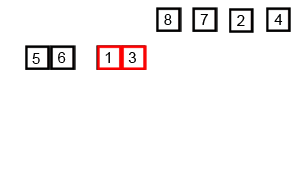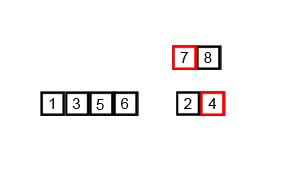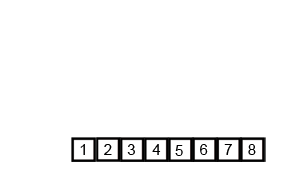
2.代码

C++：

vector<int> merge(vector<int> array) {
    if(array.size()>1){
        int middle = array.size()/2;
        vector<int> front(array.begin(), array.begin()+middle);
        vector<int> rear(array.begin()+middle, array.end());
        array = mergesort(merge(front), merge(rear));
    }
    return array;
}

vector<int> mergesort(vector<int> front, vector<int> rear) {
    int i=0,j=0;
    vector<int> sorted;
    while(i<front.size() && j<rear.size()){
        if(front[i] <= rear[j]){
            sorted.push_back(front[i]);
            i++;
        }
        else{
            sorted.push_back(rear[j]);
            j++;
        }
    }
    while(i<front.size()){
        sorted.push_back(front[i]);
        i++;
    }
    while(j<rear.size()){
        sorted.push_back(rear[j]);
        j++;
    }
    return sorted;
}

JAVA：

void merge(int[] array, int begin, int end) {
    if(array.length>1){
        int middle = (begin + end)/2;
        merge(array, begin, middle);
        merge(array, middle+1, end);
        mergesort(array, begin, middle, end);
    }
}

void mergesort(int[] array, int begin, int middle, int end) {
    int i=begin,j=middle+1,k=begin;
    int[] sorted = new int[array.length];
    while(i<=middle && j<=end){
        if(array[i] <= array[j]){
            sorted[k++] = array[i++];
        }
        else{
            sorted[k++] = array[j++];
        }
    }
    while(i<=middle){
        sorted[k++] = array[i++];
    }
    while(j<=end){
        sorted[k++] = array[j++];
    }
    for(k=begin;k<=end;k++){
        array[k] = sorted[k];
    }
}

Python：

def merge(array):
    if len(array) > 1:
        middle = int(len(array) / 2)
        front = array[:middle]
        rear = array[middle:]
        array = mergesort(merge(front), merge(rear))
    return array


def mergesort(front, rear):
    i, j = 0, 0
    result = []
    while i < len(front) and j < len(rear):
        if front[i] <= rear[j]:
            result.append(front[i])
            i += 1
        else:
            result.append(rear[j])
            j += 1
    while i < len(front):
        result.append(front[i])
        i += 1
    while j < len(rear):
        result.append(rear[j])
        j += 1
    return result

3.优化

4.评估

时间复杂度：O(nlogn)

空间复杂度：O(n)

稳定性：稳定