[学习笔记]后缀数组(Suffix Array)

后缀数组(suffix array)是一个通过对字符串的所有后缀经过排序后得到的数组。后缀数组被 Manber 和 Myers 于1990年提出, 作为对后缀树的一种替代, 更简单以及节省空间。它们也被Gaston Gonnet 于1987年独立发现, 并命名为“PAT数组”。

后缀数组有很多奇妙的性质, 这些性质可以帮助我们解决很多字符串问题(或者出串串题虐死别人)。

板子题:

P3809 【模板】后缀排序

\(O(n \log^2 n)\) 做法

后缀 \(i\) 代指以第 i 个字符开头的后缀, 本文规定字符串下标从 \(1\) 开始, 后文都将使用数组式下标。

首先朴素的想, 将 \(n\) 个后缀直接塞进 string 数组内大力 sort, 很不幸 STL 提供的 string 类型比较字典序的复杂度为 \(O(n)\), 我们只能得到 \(O(n^2 \log n)\) 的暴力。

回想一下我们比较字符串的字典序的过程：

1.从第一个字符开始比较。

2.如果当前字符不相等, 就直接比较这两个字符, 即可得出答案。

3.否则, 继续比较下一个字符。

这个过程实际上就是在寻找两个字符串的最长公共前缀, 而下一个字符就一定不相等。最长公共前缀是具有单调性的, 哈希上二分一下就能 \(O(\log n)\) 比较字典序, 这样我们的算法就优化到了 \(O(n \log^2 n)\)。这个复杂度已经可以通过洛谷的模板题了(代码)。

复杂度瓶颈在排序和求 LCP, 不好优化, 考虑另一种 \(O(n \log^2 n)\) 的做法:

先按照每个后缀的第一个字符排序。对于每个字符, 我们按照字典序给一个排名(当然可以并列), 这里称作关键字。

接下来我们再把相邻的两个关键字合并到一起, 就相当于根据每一个后缀的前两个字符进行排序。想想看, 这样就是以第一个字符(也就是自己本身)的排名为第一关键字, 以第二个字符的排名为第二关键字, 把组成的新数排完序之后再次标号。没有第二关键字的补零。

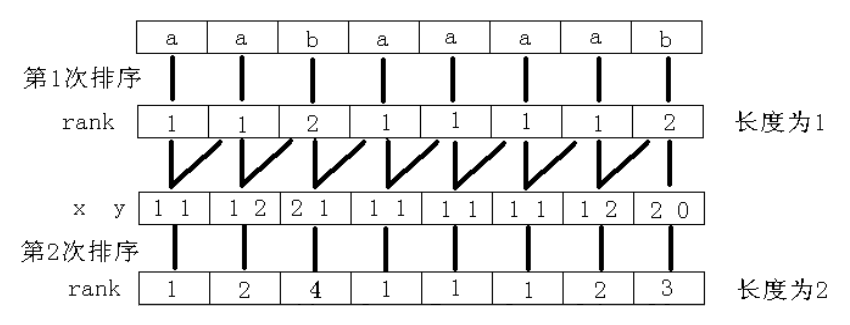
既然是倍增, 就要有点倍增的样子。接下来我们对于一个在第 \(i\) 位上的关键字, 它的第二关键字就是第 \((i+2)\) 位置上的, 联想一下, 因为现在第 \(i\) 位上的关键字是后缀 \(i\) 的前两个字符的排名, 第 \(i+2\) 位置上的关键字是后缀 \(i+2\) 的前两个字符的排名, 这两个一合并, 不就是后缀 \(i\) 的前四个字符的排名吗？方法同上, 排序之后重新标号, 没有第二关键字的补零。同理我们可以证明, 下一次我们要合并的是第 \(i\) 位和第 \(i+4\) 位, 以此类推即可……

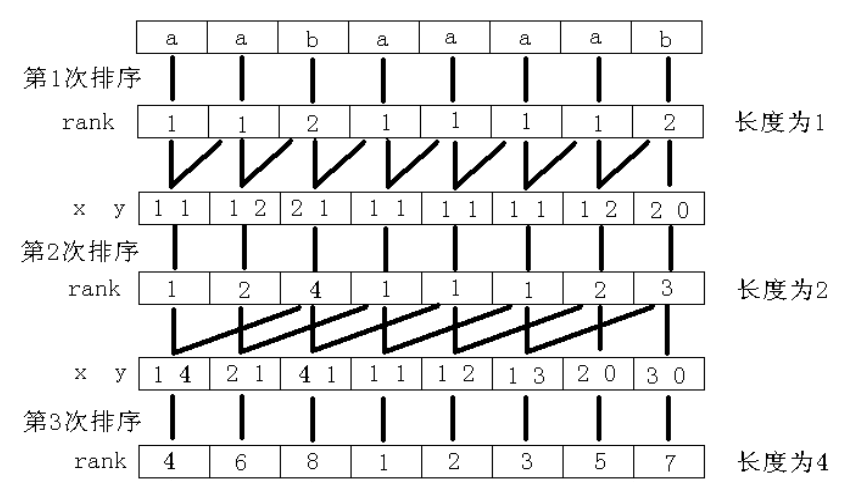
那么我们什么时候结束呢？很简单, 当所有的排名都不同的时候我们直接退出就可以了, 因为已经排好了。最多倍增 \(O(\log n)\) 次, 使用 sort 排序, 总复杂度 \(O(n \log^2 n)\)。

这种方法的常数远小于上一种方法, 因为倍增中每次排序都会使后缀数组更有序, sort 越有序跑得越快, 排好后可以提前退出, 在洛谷上跑的挺快的 (代码)。

\(O(n \log n)\) 做法

复杂度还是一样, 复杂度瓶颈是倍增和排序好像也没啥变化, 除了常数变小, 这种做法还有什么好处吗?

当然有！排序的关键字由字典序变为了排名, 排名的值域是 \(O(n)\) 的, 立刻联想到计数排序。关键字有两个也好办, 多关键字计数排序就是基数排序, 常数个关键字的基数排序时间复杂度还是 \(O(n)\), 排序两次就成了(代码)。

因为两次计数排序需要很多转换, 代码里很多层循环, 总复杂度是常数略大的 \(O(n \log n)\), 并没有与上面的小常数 \(O(n \log^2 n)\) 拉开太大差距。

\(O(n)\) 做法

还没有学, 先在这里挖个坑, 以后学了再补。

参考：

1.后缀数组学习笔记 - xMinh

2.【数据结构与算法】字符串匹配（后缀数组） - gonghr

3.后缀数组简介 - oiwiki