组合容斥做题笔记
本来在纸上来着,但是太不堪入目了。
挑一些我认为比较有趣的写上去。
求出第 \(k(k\le 10^9)\) 的不含大于 \(1\) 的平方数因子的数。
二分答案,判断 \([1,x]\) 中满足条件的数个数。
考虑 \([1,\lfloor\sqrt n\rfloor]\) 中的所有质数,答案可以容斥得到。注意到容斥的形式是加上一个有质数因子的,减去有两个质数因子的……。联想到 \(\mu\) 函数,发现 \(\mu\) 函数就是我们的容斥系数。
并且发现,枚举数大于 \(\lfloor\sqrt x\rfloor\) 时没有意义,于是筛出 \(1\) 到 \(\sqrt x\) 的 \(\mu\) 然后就做完了。
#include<iostream>
int t, n, p[50005], ip[50005], u[50005], c;
int main(){
u[1] = 1; for(int i = 2; i <= 50000; i++){
if(!ip[i]) p[++c] = i, u[i] = -1;
for(int j = 1; j <= c && i * p[j] <= 50000; j++){
ip[i * p[j]] = 1;
if(i % p[j]) u[i * p[j]] = - u[i];
else break;
}
}
auto ck = [](int x){
int rs = 0;
for(int i = 1; i * i <= x; i++)
rs += u[i] * (x / (i * i));
return rs >= n;
}; std::cin >> t; while(t--){
std::cin >> n;
long long l = n, r = 1644934082ll, md, rs;
while(l <= r){
md = l + r >> 1;
if(ck(md)) rs = md, r = md-1;
else l = md + 1;
} std::cout << rs << '\n';
}
}
\(n\times m\) 的棋盘中,用 \(c\) 种颜色染色,满足每行每列至少有一个格子被染色,所有颜色都被用过的染色方案总数。
对于颜色容斥,设 \(f_i\) 表示用了 \(i\) 种颜色,满足条件的方案数,答案是 \(\sum\limits_{i=0}^c(-1)^i\left(\begin{matrix}c\\i\end{matrix}\right)f_{c-i}\)。
考虑求 \(f_i\)。对列容斥,那么 \(f_i=\sum\limits_{k=0}^{m}(-1)^k\left(\begin{matrix}m\\k\end{matrix}\right)((i+1)^k-1)^n\) 容斥系数不解释,后面的 \((i+1)^k\) 是填一行的方案数,\(-1\) 是为了让行非空。做完了。这题没必要给代码。
给定数量的若干个彩色棋子,放在 \(n\times m\) 的棋盘里,使得同一行或一列不存在不同色棋子。
设 \(f_{i,j,k}\) 表示用前 \(k\) 种颜色填了 \(i\) 行 \(j\) 列的方案数,\(g_{i,j,k}\) 表示用 \(k\) 枚同色棋子占了 \(i\) 行 \(j\) 列的方案数。
答案是 \(\sum\limits_{i=1}^n\limits\sum_{j=1}^mf_{i,j,c}\)。
\(f_{i,j,k}=\sum\limits_{l=0}^{i-1}\sum\limits_{r=0}^{j-1}f_{l,r,k-1}\times g_{i-l,j-r,a_k}\times\left(\begin{matrix}n-l\\i-l\end{matrix}\right)\times\left(\begin{matrix}m-r\\j-r\end{matrix}\right)((i-l)\times(j-r)\ge a_k)\)
\(g\) 可以表示为总方案数减去不合法的方案数。
\(g[i][j][k]=\left(\begin{matrix}i\times j\\ k\end{matrix}\right)-\sum\limits_{l=1}^i\sum\limits_{r=1}^jg[l][r][k]\times \left(\begin{matrix}i\\l\end{matrix}\right)\times \left(\begin{matrix}j\\r\end{matrix}\right)(l<i||r<j,i\times j\ge k)\)
#include<iostream>
#include<cstring>
const int p = 1e9 + 9;
int n, m, c, ans, fc[1000], iv[1000], f[31][31][251], g[31][31];
inline int qp(int a, int b){int r = 1;
for(; b; b >>= 1, a = 1ll * a * a % p)
b & 1 ? r = 1ll * r * a % p : 0; return r;
}
inline int C(int n, int m){return n<m?0:1ll*fc[n]*iv[m]%p*iv[n-m]%p;}
int main(){
std::cin >> n >> m >> c; fc[0] = iv[0] = 1;
for(int i = 1; i < 1000; i++)
fc[i] = 1ll * fc[i - 1] * i % p,
iv[i] = 1ll * iv[i - 1] * qp(i, p - 2) % p;
f[0][0][0] = 1; for(int k = 1, x; k <= c; k++){
std::cin >> x; memset(g, 0, sizeof g);
for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++)
if(i * j >= x){ g[i][j] = C(i * j, x);
for(int l = 1; l <= i; l++) for(int r = 1; r <= j; r++)
if(l < i || r < j) g[i][j] = (g[i][j] -
1ll * g[l][r] * C(i, l) % p * C(j, r) % p + p) % p;
}
for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++)
for(int l = 0; l < i; l++) for(int r = 0; r < j; r++){
int tx = i - l, ty = j - r;
if(tx * ty >= x)
(f[i][j][k] += 1ll * f[l][r][k - 1] * g[tx][ty]
% p * C(n - l, tx) % p * C(m - r, ty) % p) %= p;
}
}
for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++)
(ans += f[i][j][c]) %= p; std::cout << ans;
}
如果一个排列 \(P\) 满足对于所有的 \(i\) 都有 \(|P_i-i|\neq k\),则称排列 \(P\) 为合法的。现给出 \(n\) 和 \(k\),求有多少种合法的排列。
问题等价于以下的图中,阴影不能填且同一行一列不存在一个以上的方案数。
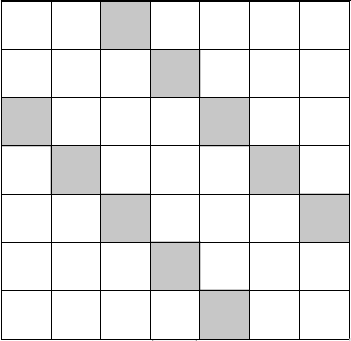
容斥,设 \(f_i\) 表示在阴影中填 \(i\) 个的方案数。答案是 \(\sum\limits_{i=0}^n(-1)^if(n-i)!\)
但是阴影中有的也不能相邻,即下图:
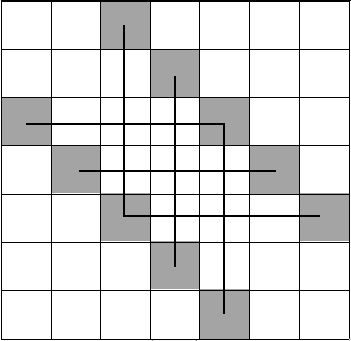
连线的不能同选。这是若干条链,把所有链拼到一起,那么拼接处可以同选,其余地方相邻的不能同时选,这是一个 dp 问题,可以 \(O(n^2)\) 了。
给你一颗 \(n\) 个点的树和 \(m\) 个限制 \(u_i,v_i\),你需要给树的点标号为 \(1\) 到 \(n\),使得任意一条树上的边 \(x,y\),存在一条限制 \(i\),使得 \(x=u_i,y=v_i\) 或 \(x=v_i,y=u_i\)。
先设一个 dp,\(f_{i,j,S}\) 表示树上 \(i\) 号点标号为 \(j\),其子树的状态是 \(S\) 的方案数。
但是这是 \(O(n^3\times3^n)\) 的,Tle 啦!
考虑一个奇怪的容斥,我们钦定只能一遍 dp 选一个 \(S\) 中的点,那么答案是 \(\sum\limits_Sf_S\times(-1)^{n-|S|}\)。
于是复杂度变成了 \(O(n^3\times 2^n)\)。
#include<iostream>
#include<cstring>
#include<vector>
int n, m, g[20][20], t[20];
long long f[20][20], ans;
std::vector<int> e[20];
inline void dfs(int x, int fa){
for(int i = 1; i <= n; i++) f[x][i] = 1;
for(auto v:e[x]) if(v != fa){
dfs(v, x); for(int j = 1; j <= n; j++){
long long s = 0;
for(int k = 1; k <= n; k++) if(g[j][k])
s += f[v][k] * (t[j] & t[k]);
f[x][j] *= s;
}
}
}
int main(){
std::cin >> n >> m;
for(int i = 1, x, y; i <= m; i++)
std::cin >> x >> y, g[x][y] = g[y][x] = 1;
for(int i = 1, x, y; i < n; i++)
std::cin >> x >> y, e[x].push_back(y), e[y].push_back(x);
for(int i = 0; i < 1 << n; i++){
int c = __builtin_popcount(i);
memset(f, 0, sizeof f), memset(t, 0, sizeof t);
for(int j = 1; j <= n; j++) t[j] = (i >> j-1) & 1;
dfs(1, 0); for(int j = 1; j <= n; j++)
ans += f[1][j] * (c & 1 ? -1 : 1);
} if(ans < 0) ans = -ans; std::cout << ans;
}
给定一颗点数是偶数的树,将树上的点两两配对,对于配对的一对点 \(u,v\),将路径 \(u\rightarrow v\) 上的边标记,求有多少种方案使得所有边都被标记了。
直接 dp 是 \(O(n^3)\) 的,考虑容斥。
钦定一个边集 \(S\) 不选的方案数是 \(f_S\),那么答案就是 \(\sum\limits_S(-1)^{|S|}f_S\)。
考虑求 \(f_S\) 这等价于把原树划分成若干个点集后,点集之内连边的方案数。
一个大小是 \(n\) 的连通块,答案是 \((n-1)\times(n-3)\times\cdots\times1\)。不妨设为 \(g_n\)。
于是设一个 dp,\(f_{i,j}\) 表示 \(i\) 子树内,与 \(i\) 相连的连通块大小是 \(j\) 的方案数,一个子树全部被覆盖的方案数(不妨记为 \(f_{i,0}\))是 \(-\sum\limits_jf_{i,j}\times g_j\),这里取负数是因为我们还需要满足这个点到他父亲的这一条边,但如果是跟则不需要考虑。
#include<algorithm>
#include<iostream>
#include<vector>
const int N = 5005, p = 1e9 + 7;
std::vector<int> e[N];
int n, f[N][N], g[N], s[N], t[N];
inline void dfs(int x, int fa){
f[x][s[x] = 1] = 1;
for(auto v:e[x]) if(v != fa){
dfs(v, x); std::fill(t+1, t+s[x]+s[v]+1, 0);
for(int i = 1; i <= s[x]; i++)
for(int j = 0; j <= s[v]; j++)
t[i+j] = (t[i+j] + 1ll * f[x][i] * f[v][j] % p) % p;
s[x]+=s[v]; for(int i=1; i<=s[x]; i++) f[x][i] = t[i];
}
for(int i = 2; i <= s[x]; i += 2)
(f[x][0] += p - 1ll * f[x][i] * g[i] % p) %= p;
}
int main(){
std::cin >> n; g[0] = 1;
for(int i = 2; i <= n; i += 2)
g[i] = 1ll * g[i - 2] * (i - 1) % p;
for(int i = 1, x, y; i < n; i++)
std::cin >> x >> y, e[x].push_back(y), e[y].push_back(x);
dfs(1, 0); std::cout << p - f[1][0];
}
三人\(a\), \(b\), \(c\)面前分别有 \(n_1\) ,\(n_2\) , \(n_3\) 张牌,
每张牌上写了\(a\),\(b\),\(c\)中的一个, 规则如下:
第一回合是\(a\)的回合,若轮到某个玩家行动时他面前没牌了,该玩家获胜 。
否则拿出牌堆中的一张牌,丢掉它,并进入该牌上写着的玩家的回合 。
游戏开始前牌的所有情况共 \(3^{n_1+n_2+n_3}\) 种,求 \(a\) 获胜的情况数。
对于操作序列来计数,因为一个操作序列相关的牌在牌堆中是相同的。而对于一个长为 \(m\) 的操作序列,剩下的 \(n_1+n_2+n_3-m\) 张牌是无限制的。
一个操作序列是合法的,当且仅当其中存在恰好 \(n_1\) 个 \(a\),不超过 \(n_2\) 个 \(b\) 和不超过 \(n_3\) 个 \(c\)。且序列的最后一项是 \(a\)。我们枚举非 \(a\) 牌的个数,则方案数为:
\(\left(\begin{matrix}k+n_1-1\\k\end{matrix}\right)\sum\limits_{i=0}^k[i\le n_2][k-i\le n_3]\left(\begin{matrix}k\\i\end{matrix}\right)\)
这个式子左边是把 \(a\) 和非 \(a\) 混合到一起,后面是瓜分非 \(a\) 牌的过程。
后面的式子很烦,考虑对其递推:
\(S_k=\sum\limits_{i=0}^k[i\le n_2][k-i\le n_3]\left(\begin{matrix}k\\i\end{matrix}\right)=\sum\limits_{k-n_3\le i\le n_2}\left(\begin{matrix}k\\i\end{matrix}\right)\)
\(S_k=\sum\limits_{k-n_3\le i\le n_2}\left(\begin{matrix}k-1\\i\end{matrix}\right)+\left(\begin{matrix}k-1\\i-1\end{matrix}\right)\)
\(=\sum\limits_{k-n_3\le i\le n_2}\left(\begin{matrix}k-1\\i\end{matrix}\right)+\sum \limits_{k-n_3-1\le i\le n_2-1}\left(\begin{matrix}k-1\\i\end{matrix}\right)\)
\(=2S_{k-1}-\left(\begin{matrix}k-1\\k-n_3-1\end{matrix}\right) -\left(\begin{matrix}k-1\\n_2\end{matrix}\right) \)
于是答案等于 \(\sum\limits_{k=0}^{n_2+n_3}3^{n_1+n_2+n_3-k}\left(\begin{matrix}n_1-1+k\\k\end{matrix}\right)S_k \)。
#include<iostream>
const int p = 1e9+7, N = 1e6+10;
int n1, n2, n3, ans, f[N], v[N], s[N];
inline int qp(int a, int b){int r = 1;
for(; b; b >>= 1, a = 1ll * a * a % p)
b & 1 ? r = 1ll * r * a % p : 0; return r;
}
inline int c(int n, int m){return n<m||m<0?0:1ll*f[n]*v[m]%p*v[n-m]%p;}
int main(){
std::cin >> n1 >> n2 >> n3; f[0] = v[0] = s[0] = 1;
for(int i = 1; i <= n1+n2+n3; i++)
f[i] = 1ll * f[i - 1] * i % p,
v[i] = 1ll * v[i - 1] * qp(i, p - 2) % p;
for(int k = 1; k <= n2 + n3; k++)
s[k] = ((2ll*s[k-1]%p-c(k-1,k-1-n3)-c(k-1,n2))%p+p)%p;
for(int k = 0; k <= n2+n3; k++)
ans = (ans + 1ll*qp(3,n2+n3-k)*c(n1-1+k,k)%p*s[k]%p)%p;
std::cout << ans;
}
求所有长为 \(n\),字符集大小为 \(m\) 的字符串中,每个字符串的本质不同子串数的和。
发现有的串的性质很相同,于是我们枚举子串的长度。对于长度是 \(x\) 的子串,枚举其出现位置的下标 \(S\),若我们知道有多少串满足 \(S\) 那么这种长度的串的答案是 \(\sum\limits_{S}(-1)^{|S|}f_S\)。
考虑到对于一个 \(S\),他的限制等价于整个串的一些部分是相同的,一些部分是不同的,把相同限制的位置合到一起,可以并查集实现,然后就是一个 \(m\) 的这么多次方。
#include<iostream>
const int p = 1e9 + 7;
inline int qp(int a, int b){int r = 1;
for(; b; b >>= 1, a = 1ll * a * a % p)
b & 1 ? r = 1ll * r * a % p : 0; return r;
}
int n, m, ans, f[25];
inline int fd(int x){return f[x]==x?x:f[x]=fd(f[x]);}
inline void cal(int x){
int a = 1 << n-x+1, b = (1<<x)-1;
for(int i = 1; i < a; i++){
int c = 0, g = 0; for(int j = 0; j < x; j++) f[j] = j;
for(int j = 0; j < n; j++){
c = (c<<1) | ((i>>j)&1); c &= b;
if(!c) ++g; else{
int t = c-(c&-c), fa=fd(__builtin_ctz(c));
while(t) f[fd(__builtin_ctz(t))]=fa, t -= t&-t;
}
}
for(int j = 0; j < x; j++) g += j == f[j]; g = qp(m, g);
if(__builtin_parity(i)) ans=(ans+g)%p; else ans=(ans-g+p)%p;
}
}
int main(){
std::cin >> n >> m;
for(int i = 1; i <= n; i++) cal(i);
std::cout << 1ll * ans * qp(qp(m, n), p - 2) % p;
}
\(2^n\) 个人按满二叉树的形式进行淘汰赛,你是第 \(1\) 个人。
有 \(m\) 个数 \(a_1\cdots a_m\)。你可以打败不在 \(a\) 中的人,但是会被 \(a\) 中的人打败。
如果比赛的两个人都不是 \(1\),那么编号小的获胜。
求所有 \(2^n!\) 种排列中,你获胜的方案。
手画一下,发现 \(1\) 的位置无足轻重,随便挑一个位置乘上 \(2^n\) 就可以。再推一下你要交战的人,发现这相当于把所有的 \(2\cdots 2^n\) 放到大小为 \(1,2,4\cdots2^{n-1}\) 的集合中且每组的最小值不是 \(a\) 中的数的方案数。将这些集合记为第 \(0,1\cdots n-2\) 个。
最小值不是 \(a\),这个限制很困难啊,于是考虑转化,容斥一下,设 \(g_S\) 表示 \(S\) 中的这些集合最小值是 \(a\) 的方案数。
则 \(ans=2^n\times\sum\limits_S(-1)^{|S|}g_S\)。
因为我们要求最小值,所以把 \(a\) 降序排列,后来的 \(a\) 的限制一定更紧。
不妨设 \(f_{i,S}\) 表示填到 \(a\) 中第 \(i\) 个,\(S\) 满足了最小值是 \(a\) 的限制,其余随便填的方案数。发现这个状态里,\(S\) 刚好是已经填过的数的数量。
转移有两种:
把 \(a_i\) 放到已经填过的组里,则 \(f_{i,S}=f_{i,S}+f_{i-1,S}\)
放到第 \(k\) 个组中,找 \(2^k-1\) 个比它大的随便排列放进去:\(f_{i,S|2^k}=f_{i,S|2^k}+f_{i-1,S}\times\left(\begin{matrix}2^n-S-a_i\\2^k-1\end{matrix}\right)\times 2^k!\)
那么 \(g_S = f_{m,S}\times(2^n-1-S)!\),不在 \(S\) 中的数可以随便排。做完了。
#include<iostream>
#include<algorithm>
const int p = 1e9 + 7, N = 5e5 + 10;
int n, m, a[20], fc[N], iv[N], f[20][N];
inline int qp(int a, int b){int r = 1;
for(; b; b >>= 1, a = 1ll * a * a % p)
b & 1 ? r = 1ll * r * a % p : 0; return r;
}
inline int c(int n, int m){return n<m||m<0?0:1ll*fc[n]*iv[m]%p*iv[n-m]%p;}
int main(){
std::cin >> n >> m; fc[0] = iv[0] = 1;
for(int i = 1; i <= m; i++) std::cin >> a[i];
for(int i = 1; i <= 5e5; i++)
fc[i] = 1ll * fc[i - 1] * i % p,
iv[i] = 1ll * iv[i - 1] * qp(i, p-2) % p;
std::reverse(a + 1, a + m + 1); f[0][0] = 1;
for(int i = 1; i <= m; i++) for(int s = 0; s < 1 << n; s++){
(f[i][s] += f[i - 1][s]) %= p;
for(int k = 0; k < n; k++) if(!((s>>k)&1))
(f[i][s|(1<<k)] += 1ll*f[i-1][s]*
c((1<<n)-s-a[i],(1<<k)-1)%p*fc[1<<k]%p) %= p;
}
int ans = 0; for(int s = 0; s < 1 << n; s++){
int x = 1ll * f[m][s] * fc[(1<<n)-s-1] % p;
__builtin_parity(s)?(ans+=p-x)%=p:(ans+=x)%=p;
}
std::cout << 1ll * ans * (1<<n) % p;
}
对一个 \(n\) 行 \(m\) 列,初始全是 \(0\) 的矩阵,执行以下操作:
对每一行选一个 \(k_i(0\le k_i\le m)\) 将这一行最左 \(k_i\) 个数加一。
对每一列选一个 \(l_i(0\le l_i\le n)\) 将这一列最上 \(l_i\) 个数加一。
最后得到一个 \(0,1,2\) 的矩阵,求本质不同矩阵数。
考虑什么时候会算重,手画一下只有以下这种形式:
00010
00010
00010
11110
00000
这样 \(k_4=4,l_4=3\) 和 \(k_4=3,l_4=4\) 都是满足的。
将这样的地方称为“拐角”。易于证明拐角做多有 \(\min(n,m)\) 个。
设 \(f_i\) 为钦定了 \(i\) 个拐角的图的方案数。
那么 \(f_i=\left(\begin{matrix}n\\i\end{matrix}\right)\left(\begin{matrix}m\\i\end{matrix}\right)i!(n+1)^{m-i}(m+1)^{n-i}\) 这是选出 \(i\) 行 \(i\) 列然后排列一下。后面的是剩下的行和列的方案。
设 \(f'_i\) 为钦定了 \(i\) 个拐角的操作序列数,那么显然有 \(f'_i=2^if_i\)。
再设 \(g_i\) 表示恰好有 \(i\) 个拐角的操作数,有这个式子:
\(f'_i=\sum\limits_j\left(\begin{matrix}j\\i\end{matrix}\right)g_j\)。二项式反演一下有 \(g_i=\sum\limits_j\left(\begin{matrix}j\\i\end{matrix}\right)(-1)^{j-i}f'_j\)。
于是我们要求 \(\sum\limits_i\frac{g_i}{2^i}\)。推一下式子:
\(=\sum\limits_i\frac{1}{2^i}\sum\limits_j\left(\begin{matrix}j\\i\end{matrix}\right)(-1)^{j-i}f'_j\)。
\(=\sum\limits_i\frac{1}{2^i}\sum\limits_j\left(\begin{matrix}j\\i\end{matrix}\right)(-1)^{j-i}f_j2^j\)。
把求和顺序变一下:
\(=\sum\limits_jf_j\sum\limits_{i\le j}\left(\begin{matrix}j\\i\end{matrix}\right)(-1)^{j-i}2^{j-i}\)
考虑 \((1+(-2))^j=\sum\limits_{i\le j}\left(\begin{matrix}j\\i\end{matrix}\right)1^i\times(-2)^{j-i}=\sum\limits_{i\le j}\left(\begin{matrix}j\\i\end{matrix}\right)(-1)^{j-i}2^{j-i}\)。
所以原式子等于 \(\sum\limits_jf_j\times(-1)^j\)。
#include<iostream>
const int p = 998244353;
int n, m, ans, fc[500005], iv[500005];
inline int qp(int a, int b){int r = 1;
for(; b; b >>= 1, a = 1ll * a * a % p)
b & 1 ? r = 1ll * r * a % p : 0; return r;
}
inline int c(int n, int m){return n<m||m<0?0:1ll*fc[n]*iv[m]%p*iv[n-m]%p;}
int main(){
std::cin >> n >> m; fc[0] = iv[0] = 1;
for(int i = 1; i <= std::max(n, m); i++)
fc[i] = 1ll * fc[i-1] * i % p,
iv[i] = 1ll * iv[i-1] * qp(i, p-2) % p;
for(int i = 0; i <= std::min(n, m); i++){
int x = 1ll * c(n, i) * c(m, i) % p;
int y = 1ll*fc[i]*qp(m+1, n-i)%p*qp(n+1, m-i)%p;
x = 1ll * x * y % p;
if(i & 1) ans = (ans + p - x) % p;
else ans = (ans + x) % p;
}
std::cout << ans;
}
有 \(n\) 张卡,第 \(i\) 张的权值有 \(p_{i,1}\) 的概率是 \(1\),\(p_{i,2}\) 的概率是 \(2\),\(p_{i,3}\) 的概率是 \(3\),记为 \(w_i\)。
你要开始氪金抽卡(哎,原神),有 \(\frac{w_i}{\sum w}\) 的概率抽到第 \(i\) 张卡。同时有 \(n-1\) 个限制 \(u_i,v_i\),若抽完卡后,对于任意的 \(i\in[1,n-1]\),\(u_i\) 都比 \(v_i\) 先抽到,那么这次抽卡是好的。
保证将限制视为无向边,这是一颗树。求出先将所有卡的权值随好后,满足所有限制的抽卡的概率。
很烦啊,若将 \(1\) 视为根,这棵树既有内向边又有外向边。
先试试全是外向边能不能做。设一个点 \(x\) 子树的子树的权值和是 \(sm_x\),则这颗子树合法,当且仅当先抽到子树的根,且根的每个儿子各自合法。即 \(f_x=\frac{w_x}{sm_x}\prod\limits_{(x,v)\in E}f_v\)。
这个东西和子树权值和有关,设 \(f_{x,i}\) 为 \(x\) 子树,权值和是 \(i\) 的概率,这是个很经典的树 dp 问题。可以 \(O(n^2)\)。
你说得对,但是内向边很烦。处理方式是:考虑这条边是内向边的限制,等价于不考虑这条边减去这条边是外向边的概率。
这个真的很难想到,但是想到了就很显然。
#include<iostream>
#include<algorithm>
#include<vector>
#define pb emplace_back
const int p = 998244353;
std::vector <std::pair<int, int>> e[1005];
int n, ans, t[3005], iv[3005], s[1005], g[1005][3], f[1005][3005];
inline int qp(int a, int b){ int r = 1;
for(; b; b >>= 1, a = 1ll * a * a % p)
b & 1 ? r = 1ll * r * a % p : 0; return r;
}
inline void ad(int &x, int y){x += y; x >= p ? x -= p : 0;}
inline void dfs(int x, int fa){
f[x][0] = 1; for(auto [v, w]:e[x]) if(v != fa){
dfs(v, x); int sx = s[x]*3, sv = s[v]*3;
std::fill(t, t+sx+sv+1, 0);
if(w) for(int i = 0; i <= sx; i++)
for(int j = 0; j <= sv; j++)
ad(t[i+j], 1ll * f[x][i] * f[v][j] % p);
else{
int sm = 0; for(int i = 0; i <= sv; i++) ad(sm, f[v][i]);
for(int i = 0; i <= sx; i++) t[i] = 1ll * sm * f[x][i] % p;
for(int i = 0; i <= sx; i++) for(int j = 0; j <= sv; j++)
ad(t[i+j], p - 1ll * f[x][i] * f[v][j] % p);
}
for(int i = 0; i <= sx + sv; i++) f[x][i] = t[i]; s[x] += s[v];
}
int sx = s[x] * 3; std::fill(t, t+sx+4, 0);
for(int i = 0; i <= sx; i++)
ad(t[i+1], 1ll*f[x][i]*g[x][0]%p*iv[i+1]%p),
ad(t[i+2], 2ll*f[x][i]*g[x][1]%p*iv[i+2]%p),
ad(t[i+3], 3ll*f[x][i]*g[x][2]%p*iv[i+3]%p);
for(int i = 0; i <= sx+3; i++) f[x][i] = t[i]; ++s[x];
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);std::cout.tie(0);
std::cin >> n; iv[0] = 1;
for(int i = 1; i <= n*3; i++) iv[i] = qp(i, p-2);
for(int i = 1, x, y, z, t; i <= n; i++){
std::cin >> x >> y >> z, t = qp(x+y+z, p-2);
g[i][0]=1ll*x*t%p,g[i][1]=1ll*y*t%p,g[i][2]=1ll*z*t%p;
}
for(int i = 1, x, y; i < n; i++)
std::cin >> x >> y, e[x].pb(y, 1), e[y].pb(x, 0);
dfs(1, 0); for(int i = s[1]*3; ~i; i--) ad(ans, f[1][i]);
std::cout << ans;
}
唯一真神。
在 \(n\times m\times l\) 的立方体中,定义一个格子是极大的,当且仅当与这个格子至少一维相同的格子里的数都比他小。
给 \(nml\) 个格子填入 \(1\) 到 \(nml\),求出恰好有 \(k\) 个极大的点的方案数。
设我们要求的恰好有 \(i\) 个极大的点的方案数是 \(F_i\),钦定了 \(i\) 个极大的点的方案数是 \(f_i\)。答案是 \(\frac{F_k}{nml!}\),那么二项式反演有:
\(f_i=\sum\limits_j\left(\begin{matrix}j\\i\end{matrix}\right)F_j\Rightarrow F_i=\sum\limits_j\left(\begin{matrix}j\\i\end{matrix}\right)(-1)^{j-i}f_j\)。
问题转换成求 \(f\)。一些事实:
最多有 \(\min(n,m,l)\) 个极大的点,极大的点不会有任意一维相同。这两个是显然的。
有 \(i\) 个极大的数,则有 \(i\) 行,列,纵列被控制。
与此同时 \((n-i)(m-i)(l-i)\) 个格子是没有限制的,于是我们知道 \(f_i=(n^{\underline i}m^{\underline i}l^{\underline i})((nml)^{\underline{(n-i)(m-i)(l-i)}})g_i\)
其中 \(g_i\) 表示剩下的 \(nml-(n-i)(m-i)(l-i)\) 个格子中,符合规定的标号数。
这个式子的意义:前一项表示选出 \(i\) 个特殊点的过程,中间一项是对没有影响格子的标号。
于是我们来考虑 \(g_i\)。在这 \(nml-(n-i)(m-i)(l-i)\) 个格子中,一个限制 \(k\) 的意思是,所有与 \(k\) 至少一维相同的格子,都比 \(k\) 小,但是很难办的是,有可能有两个限制限制了同一个格子。于是对 \(i\) 个限制的大小也进行标号,从大到小,只考虑能确定只能被他影响的格子。
这个很难搞啊。需要发现一个性质,对于有 \(i\) 个极大点的一张图,极大点的顺序调换,不会影响被一个极大点影响的点数。很不好说,需要感性理解。
借来 @command_block 的图片

其中,不透明格子是我们的极大点,我们按极大点的大小从小到大,从外到里排列,透明格子是被与他同色的极大点控制的点,右上角有一块,这是剩下的没有被任何极大点控制的点。
易于表示出蓝色格子的数量是 \((n-1)(m-1)(l-1)-(n-2)(m-2)(l-2)\) 事实上若我们设 \(\delta_i=(n-i)(m-i)(l-i)\),这个图中从外到里第 \(i\) 层的数量是 \(\delta_{i-1}-\delta_i\)。
考虑我们的第 \(i\) 层,除了极大点,我们需要填 \(\delta_{i-1}-\delta_i-1\) 个点,填完剩下的数有 \(nml-(n-i)(m-i)(l-i)-1=\delta_0-\delta_i-1\) 个。
所以对于第 \(i\) 层,填数的方案是 \((\delta_0-\delta_i-1)^{\underline{\delta_{i-1}-\delta_i-1}}\)。
所以 \(g_i=\prod\limits_{j=1}^i(\delta_0-\delta_j-1)^{\underline{\delta_{j-1}-\delta_j-1}}\)。
写成阶乘的形式就是 \(g_i=\prod\limits_{j=1}^i\frac{(\delta_0-\delta_j-1)!}{(\delta_0-\delta_{j-1})!}\)。
可以把他化成 \((\delta_0-\delta_i-1)!\prod\limits_{j=1}^{i-1}\frac{1}{\delta_0-\delta_j}\)。
于是 \(f_i=(n^{\underline i}m^{\underline i}l^{\underline i})((nml)^{\underline{(n-i)(m-i)(l-i)}})(\delta_0-\delta_i-1)!\prod\limits_{j=1}^{i-1}\frac{1}{\delta_0-\delta_j}\)
\(=(n^{\underline i}m^{\underline i}l^{\underline i})\frac{(nml)!}{(nml-\delta_i)!}(nml-\delta_i-1)!\prod\limits_{j=1}^{i-1}\frac{1}{nml-\delta_j}\)
\(=(n^{\underline i}m^{\underline i}l^{\underline i})\frac{(nml)!}{nml-\delta_i}\prod\limits_{j=1}^{i-1}\frac{1}{nml-\delta_j}\)
\(=(n^{\underline i}m^{\underline i}l^{\underline i})(nml)!\prod\limits_{j=1}^{i}\frac{1}{nml-\delta_j}\)
因此答案:
\(ans=\frac{F_k}{(nml)!}=\frac{1}{(nml)!}\sum\limits_i(-1)^{i-k}\left(\begin{matrix}i\\k\end{matrix}\right)f_i\)。
\(f_i\) 里面有一个 \((nml)!\),把他卸掉。
\(f'_i=(n^{\underline i}m^{\underline i}l^{\underline i})\prod\limits_{j=1}^{i}\frac{1}{nml-\delta_j}\)
故 \(ans=\sum\limits_i(-1)^{i-k}\left(\begin{matrix}i\\k\end{matrix}\right)f'_i\)
发现求出 \(f'_1\cdots f'_k\) 的瓶颈在于求出一堆东西的逆元,可以套用这题。
#include<iostream>
const int p = 998244353, N = 5e6 + 10;
inline int qp(int a, int b){int r = 1;
for(; b; b >>= 1, a = 1ll * a * a % p)
b & 1 ? r = 1ll * r * a % p : 0; return r;
}
int n, m, l, k, ans, q, iv[N], v[N], s[N], sv[N], Iv[N];
inline int f(int x){return 1ll*(n-x)*(m-x)%p*(l-x)%p;}
int main(){
iv[1] = 1; for(int i = 2; i <= 5e6; i++)
iv[i] = 1ll * (p-p/i) * iv[p % i] % p;
int T; std::cin >> T; while(T--){
std::cin >> n >> m >> l >> k; s[0] = 1;
ans = 0; q = std::min(std::min(n, m), l);
for(int i = 1; i <= q; i++)
v[i] = (f(0) - f(i) + p) % p,
s[i] = 1ll * s[i - 1] * v[i] % p;
sv[q] = qp(s[q], p - 2); for(int i = q; i; i--)
Iv[i] = 1ll * sv[i] * s[i - 1] % p, sv[i - 1] = 1ll * sv[i] * v[i] % p;
int t = 0, sm = 1;
for(int i = 1; i <= q; i++){
sm = 1ll * sm * f(i - 1) % p * Iv[i] % p;
t = i==k ? 1 : (p - 1ll * t * i % p * iv[i - k] % p) % p;
ans = (ans + 1ll * t * sm % p) % p;
}
std::cout << ans << '\n';
}
}
完结撒花,玩星铁去。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号