莫队算法及其的一些简单应用

$$\textbf{莫队算法及其的一些简单应用}$$

一. 引述

莫队算法，由信息学奥赛中国国家集训队队长莫涛首次归纳提出一般形式，由后人推广得以扩展\(^{(1)}\)。通过挖掘一些根号相关的性质，可在根号相关时间复杂度内离线解决序列问题。

二. 引入

我们以如下问题为例，来探讨莫队算法的一般形式，为简化形式，以下假设询问数与序列规模同阶。

\(\text{prob.1}\) 对于长为 \(n\) 的给定序列 \(a\)。\(q\) 次询问给定 \(l,r\)，求出 \(a_l\) 到 \(a_r\) 这段中不同元素的个数。

以上问题显然可以在 \(O((n+q)\log n)\) 复杂度内解决\(^{(2)}\)。
我们不妨挖掘这个问题的一些性质。在暴力算法中，对于每一个询问，我们会遍历该区间的所有元素，使用桶来统计元素个数。在这个过程中：显然，如果我们知道区间 \([l,r]\) 的结果，可以 \(O(1)\) 得到 \([l,r+1],[l,r-1],[l-1,r],[l+1,r]\) 的结果，总结得：

\(\text{nat.1}\) 该问题具有可在 \(O(1)\) 复杂度内收缩或者扩张区间并统计答案的性质。

三. 算法简述

利用 \(\text{nat.1}\) 我们设计如下算法：

\(\text{algorithm.1}\) 顺序统计询问的答案，在当前询问统计完毕时暴力移动左右区间的指针并统计答案。

以上算法的最劣时间复杂度显然是 \(O(nq)\)，因为两次询问间指针的移动次数规模最大是 \(O(n)\)。
在 \(\text{algorithm.1}\) 中，由于我们不能保证询问之间转移时指针移动次数规模，因而带来较大的时间复杂度开销。

为了获得更优复杂度，我们需要优化指针的移动次数总和。

\(\text{prob.2}\) 最优的指针移动次数该如何计算？

不妨形象化地描述以上算法。在二维平面中，以 \(l\) 作为横轴坐标，以 \(r\) 作为纵轴坐标，以二维点 \((l_i,r_i)\) 代表询问 \([l_i,r_i]\)，显然：两个询问之间的指针移动次数可转换为平面内两个点的曼哈顿距离。

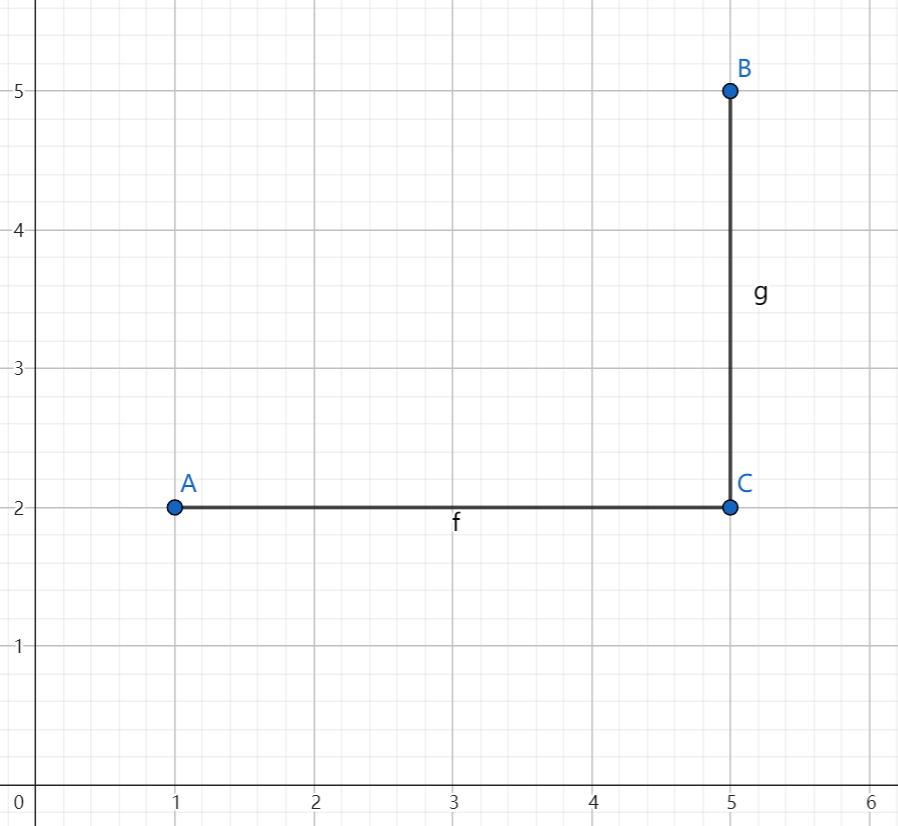
例如，询问 \(A[1,2]\) 到询问 \(B[5,5]\) 的转移次数为 7。

显然原问题等价于求出平面上若干个点的曼哈顿距离生成树，我们可以在 \(O(q\log q)\) 的复杂度内解决\(^{(3)}\)，按照这种策略优化最终的时间复杂度被证明为 \(O(n\sqrt{q})\)\(^{(4)}\)。

\(\text{algorithm.2}\) 可以在 \(O(q\log q+n\sqrt{q})\) 复杂度内解决上述问题。

不过莫涛实际上提出了一种更简单的处理方式：

\(\text{algorithm.3}\) 对于原序列从左到右分块，不妨设块长为 \(B\) 以询问左端点所在块的编号为第一关键字，以右端点的值为第二关键字排序，并将排序后的序列作为操作序列。

以下用数形结合的方式证明该算法的复杂度：

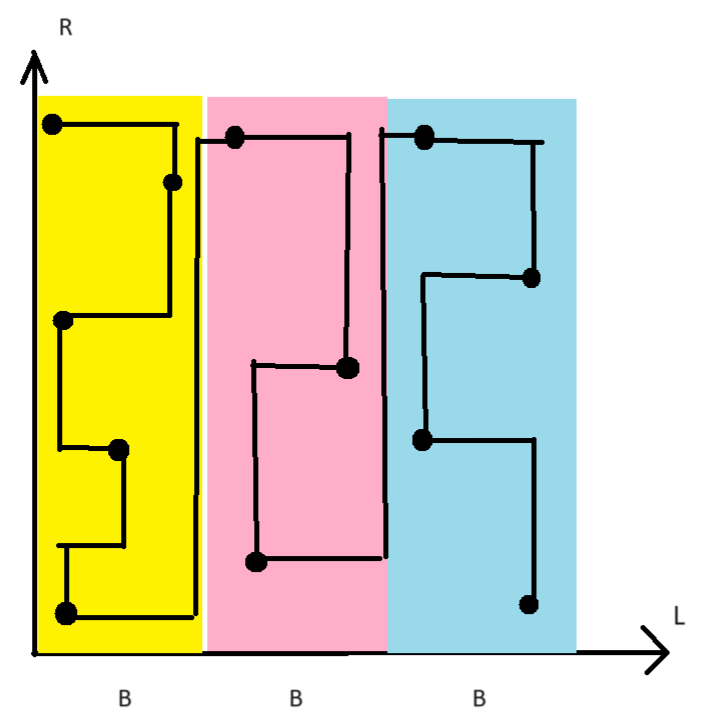
平面上的黑点是我们所要的若干个询问，
不同颜色的区间是对于序列分的不同的块，
黑色的线条是指针移动的路径

我们需要统计指针移动次数的规模，等价于该图上黑色线段的总长度，分为两部分计算：
\(1.\) 移动 \(r\) 指针的复杂度，体现为图中的竖线，显然在单个块内移动不超过 \(O(n)\)，总共分了 \(\frac{n}{B}\) 个块，这部分的复杂度是 \(O(n\times\frac{n}{B})\)
\(2.\) 移动 \(l\) 指针的复杂度，体现为图中的横线，显然由一个点到下一个点的横坐标差不超过 \(O(B)\) 总共有 \(q\) 个询问，这部分的复杂度为 \(O(q\times B)\)

总体复杂度为 \(O(q\times B + n\times\frac{n}{B})\) 显然在 \(B=\frac{n}{\sqrt q}\) 时最优取得 \(O(n\sqrt q)\)

\(\text{Lemma.1 algorithm.3}\) 的时间复杂度为 \(O(n\sqrt q)\)

综上，我们已经证明了后者实现的复杂度并不会比前者更劣。

四. 扩展和一些简单应用

\(1.\) 有关复杂度的扩展

以上的探讨基于更新答案的复杂度为 \(O(1)\)，推广之：我们设更新答案的复杂度为 \(O(A)\)，仿照 \(\text{Lemma.1}\) 的证明我们易于得到一下引理：

\(\text{Lemma.2}\) 若单词更新答案的复杂度是 \(O(A)\)，使用莫队算法的时间复杂度是 \(O(n\sqrt{q}A)\)

\(2.\) 适用范围
\((1).\) 显然，莫队是一种离线算法，不能解决强制在线问题。
\((2).\) 统计的答案一定与区间有关。

\(3.\) 高维莫队

我们不妨来考虑一个更复杂的问题

\(\text{prob.3}\) 在问题一的基础上，在询问中插入单点修改若干个修改操作，注意单次修改会对后面所有的询问有影响。\(^{(5)}\)，默认操作规模和序列规模同阶。

与问题一不同，问题二的一个询问形如 \([l,r,t]\)，分别表示左端点，右端点，时间（处于第几次修改操作之后）。而且显然，三个维度的修改都可以 \(O(1)\) 修改答案，具有可以使用莫队算法的性质。

我们是否可以仿照莫队的一般做法，来解决这样的问题？

答案是可以的，我们把一组询问 \([l,r,t]\) 视为三维空间上的一个点，问题等价于是要求得更优的策略遍历顺序使得指针在三维空间上的移动次数尽可能少，由此我们可以设计出如下算法：

\(\text{algorithm.4}\) 将所有的询问以 \(l\) 所在块的编号为第一关键字，\(r\) 所在块的编号为第二关键字，\(t\) 为第三关键字排序，将排序后的序列作为操作序列。

仿照 \(\text{Lemma.1}\) 的证明，令 \(B\) 表示分块的块长，复杂度为 \(O(qB+\frac{n^2}{B})\)，显然在 \(B=\frac{n}{\sqrt[3]{q}}\) 是有最优复杂度 \(O(n\times q^{\frac{2}{3}})\)\(^{(6)}\)。

发现性质，我们显然可以用比 \(O(n^2)\) 的复杂度更优的做法解决若干维度上的问题：

具体地，我们推广：

在解决 \(k\) 维莫队的问题时，设块长为 \(B\)，在最终的复杂度分析中令 \(k\) 为常数。

前 \(k-1\) 维按照块编号排序，最后一维直接排序，总共有 \(\frac{n^{k-1}}{B^{k-1}}\) 种所在块的情况，块内移动的复杂度时 \(O(n)\)，这部分是 \(O(\frac{n^k}{B^{k-1}})\)
处理询问之间的转移时，单维的复杂度是 \(O(B)\)，总共有 \(O(q)\) 的询问，要挪动 \(k-1\) 维，这部分是 \(O((k-1)\times nq)\)。

显然有总复杂度为 \(O(\frac{n^k}{B^{k-1}}+(k-1)\times nq)\)。

使用均值不等式，显然有当 \(B=\frac{n}{\sqrt[k]{q}}\) 时取得最优复杂度为 \(O(n\times q^{\frac{k-1}{k}})\)。

\(\text{Lemma.3}\) 使用莫队算法解决 \(k\) 维问题的理论最优时间复杂度为 \(O(n\times q^{\frac{k-1}{k}})\)，此时有莫队的块长为 \(\frac{n}{\sqrt[k]{q}}\)。

注：具体实现时，可能会因为各维度规模不同等对常数有一定影响，需要对细节做一定处理。但是莫队算法的复杂度显然正确，作为理论上界存在\(^{(6)}\)。

\(4.\) 莫队二次离线

我们来考虑这么一个问题：

\(\text{prob.4}\) 给定长为 \(n\) 的序列 \(a\)，\(q\) 次询问区间 \([l,r]\) 的逆序对数\(^{(7)}\)。

仿照一般的二维莫队，使用树状数组或者值域分块来统计答案，可以做分别到 \(O(n\sqrt{q}\log n)\) 与 \(O(n^2)\)，较劣复杂度来源于更新区间时，我们必须知道区间内数的有关信息。尝试寻找更优的算法，以右端点向右扩展为例。

不妨设更新前的区间为 \([l,r-1]\)，我们需要知道原区间中比 \(a_r\) 大的元素个数，形式化地，我们设 \(f(a,b,x)\) 为区间 \([a,b]\) 内，比 \(a_x\) 大的元素个数，即要求 \(f(l,r-1,r)\)。

发现该式显然等于 \(f(1,r-1,r)-f(1,l-1,r)\) 的差分。不妨将这样的贡献式也离线下来。前者显然便于统计，相当于原序列一个长为 \(r\) 的前缀的逆序对数，固定左端点，右端点向右移动，显然有 \(O(n\log n)\) 或 \(n\sqrt{n}\)。取决于使用树状数组或是值域分块。

考虑后者如何计算，\(f\) 函数的形式形如前缀对点的贡献，考虑对前缀的长度扫描线，从左到右扫过一遍，统计与这个前缀有关的所有右端点的贡献。显然只需要 \(O(n)\) 次更新数据结构，计算共 \(n\sqrt{q}\) 种贡献，可以使用 \(O(\sqrt{n})\) 更新，\(O(1)\) 查询的值域分块，则只需要 \(O(n\sqrt{n}+n\sqrt{q})\)。显然左右端点的左移与右移都可以差分成为这样的贡献式，我们可以用 \(O(n\sqrt{n}+n\sqrt{q})\) 的复杂度解决\(^{(8)}\)。

回顾上面的过程，我们可以总结得到以下算法。

\(\text{algorithm.5}\) 对于一类莫队问题，如果所统计的答案与区间元素有关且可差分，我们可以把贡献式拆开并离线计算。若存在做法使得更新答案的复杂度为 \(O(A)\)，查询的复杂度是 \(O(B)\)一般莫队的复杂度为 \(O(n\sqrt{q}A+qB)\)，通过莫队二次离线的做法，时间复杂度应为 \(O(nA + n\sqrt{q}B)\)。

参考资料：

\(1:\) 来源：OI-WIKI （https://oi-wiki.org/misc/mo-algo-intro/）
\(2:\) 来源：Luogu （https://www.luogu.com.cn/problem/solution/P1972）
\(3:\) 来源：CSDN (https://blog.csdn.net/qq_41848675/article/details/99887230)
\(4:\) 来源：OI-WIKI （https://oi-wiki.org/misc/mo-algo/#复杂度分析）
\(5:\) 来源：Luogu （https://www.luogu.com.cn/problem/P1903）
\(6:\) 具体证明即调整策略：Luogu （https://www.luogu.com.cn/blog/lzqy/k-mo-dui）
\(7:\) 来源：Luogu （https://www.luogu.com.cn/problem/P5047）
\(8:\) 参考：Luogu （https://www.luogu.com.cn/blog/Soulist/solution-p5047）