[Machine Learning] 使用经典线性回归模型实现房价预测
一、内容实现概述
本文主要讲述使用scikit-learn库内置的线性回归模型,实现房价预测
预测房价实现过程如下:
- 导入所需库:预先导入pandas、matplotlib以及scikit-learn库
- 导入数据:使用pandas库的文件解析方法read_csv(),读取房价文件数据
- 数据预处理:对房价数据进行预处理,获得特征数据与目标数据
- 数据分割:使用sklearn库的数据分割方法对步骤3中的数据进行比例分割,得到训练集和测试集数据
- 构建线性回归模型:调用sklearn库的线性模型类LinearRegression构建模型
- 训练模型:调用sklearn库的fit()方法对训练集数据进行训练
- 预测模型:调用sklearn库的predict()方法对测试集数据进行预测
- 绘制预测结果:调用matplotlib库的plot()与show()进行绘制并展示预测结果
- 评估模型:由于该模型是回归模型,所以调用sklearn库的均方误差评估方法
mean_squared_error()进行评估
注:
- 在Python中使用(导入)pandas库时,需要先安装,本实现使用的是pip命令安装 pip install pandas
- 在Python中使用(导入)matplotlib库时,需要先安装,本实现使用的是pip命令安装 pip install matplotlib
- 在Python中使用(导入)scikit-learn框架时,需要先安装,本实现使用的是pip命令安装 pip install -U scikit-learn
- 预先准备好的房价数据BostonHousing.csv
- Scikit-Learn官方教程
二、代码实现
注:源代码地址
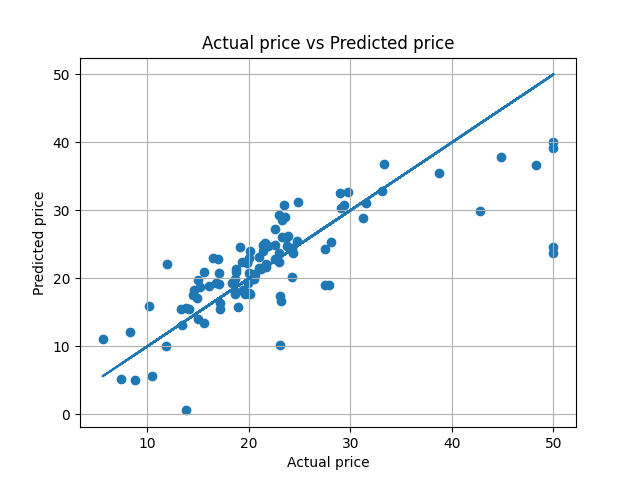
# 主题:使用线性回归实现波士顿房价预测 # 任务:找到这些指标(特征)与房价(目标)之间的关系 import pandas as pd import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error # 第一步:导入房价数据 # r为转义字符 house_data = pd.read_csv(r"regression\\linear-regression\\boston-house-prediction\\BostonHousing.csv") # 第二步:数据预处理 features = house_data.drop("medv", axis=1) prices = house_data['medv'] # 第三步:分割数据 # 设置这个随机状态(random_state)是为了保证数据集的数据“不随机” # 因为设置random_state的目的就是确保每次运行分割程序时,获得完全一样的训练集和测试集。否则,同样的算法模型在不同的训练集和测试集上的效果不一样。如果每次都随机抽样,那么在确定模型和初始参数后,你会发现,模型每运行一次,就会得到不同的预测准确率(因为模型性能通常都对训练集敏感),从而使得调参无法有效进行 # 可以这样理解,每个随机状态(random_state,即某个整数值)都代表一批不同的训练集和测试集。如果它的值不变,无论程序运行多少次,获取的都是固定的一批训练集和测试集,这种稳定性为我们进行模型调参提供了方便 # 一旦模型调参完毕,这个值就不需要设置了。如果不设置这个值,就会启用它的默认值None。一旦这个值被设置为None,就启用np.random作为随机种子,即默认以系统时间为随机种子。我们知道,时光荏苒,每时每刻的系统时间都不同,反而让样本的抽取更趋近随机抽样状态。 X_train, X_test, y_train, y_test = train_test_split(features, prices, test_size=0.2, random_state=0) # 第四步:导入线性回归模型 model = LinearRegression() # 第五步:训练模型 model.fit(X_train, y_train) # 第六步:预测模型 y_pred = model.predict(X_test) print("特征权重:", model.coef_) print("截距:", model.intercept_) # 第七步:绘制预测结果 plt.scatter(y_test, y_pred) plt.xlabel("Actual price") plt.ylabel("Predicted price") plt.title("Actual price vs Predicted price") plt.grid() plt.plot(y_test, y_test) plt.show() # 第八步:评估模型 # 由于回归分析的目标值是连续值,因此我们不能用准确率之类的评估标准来衡量模型的好坏,而应该比较预测值(Predict)和实际值(Actual)之间的差异程度。 # 其中,均方误差(mean-square error,简称MSE)是最常见的评估标准之一,具体公式见该目录下的'mean_squared_error.png' mse = mean_squared_error(y_test, y_pred) print("MSE = ", mse)
三、运行结果



 浙公网安备 33010602011771号
浙公网安备 33010602011771号