slam十四讲(二)李群李代数
李群
群(Group)是一种集合加上一种运算的代数结构。我们把集合记作 A,运算记作 ·,G = (A, ·)
性质:
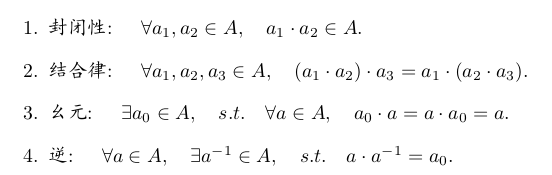
特殊正交群 SO(n) 也就是所谓的旋转矩阵群,其中 SO(2) 和 SO(3) 最为常见。
特殊欧氏群 SE(n) 也就是前面提到的 n 维欧氏变换,如 SE(2) 和 SE(3)。
李代数:
李代数由一个集合 V,一个数域 F 和一个二元运算 [, ] 组成。如果它们满足以下几条
性质,称 (V, F, [, ]) 为一个李代数,记作 g。
性质:
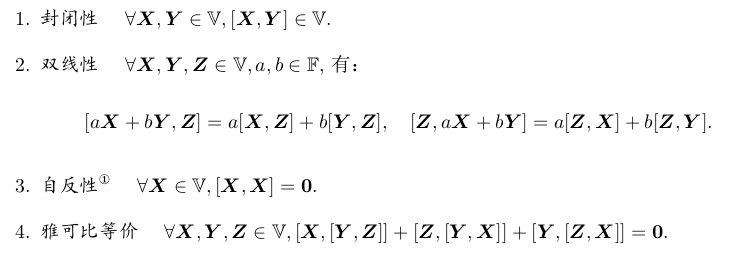
so(3):
SO(3) 对应的李代数是定义在 R 3上的向量,我们记作 φ。
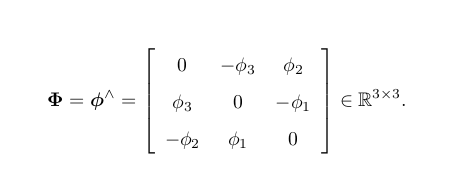
在此定义下,两个向量 φ 1 , φ 2 的李括号为:
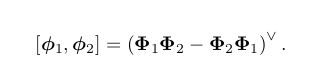
所以
so(3) = {φ ∈ R 3 , Φ = φ ∧ ∈ R 3×3 .}
它与 SO(3) 的关系由指数映射给定:
R = exp(φ ∧ ).
se(3):
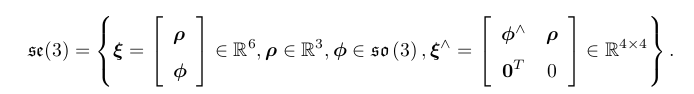
[ξ 1 , ξ 2 ] = (ξ 1 ∧ ξ 2 ∧ − ξ 2 ∧ ξ 1 ∧ ) .
SO(3) 上的指数映射:
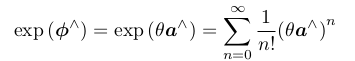
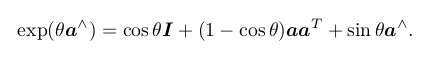
so(3) 实际上就是由所谓的旋转向量组成的空间,而指数映射即罗德里格斯公式。通过它们,我们把
so(3) 中任意一个向量对应到了一个位于 SO(3) 中的旋转矩阵。反之,如果定义对数映射,
我们也能把 SO(3) 中的元素对应到 so(3)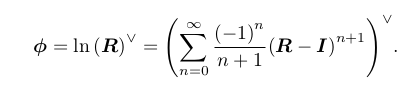
SE(3) 上的指数映射:
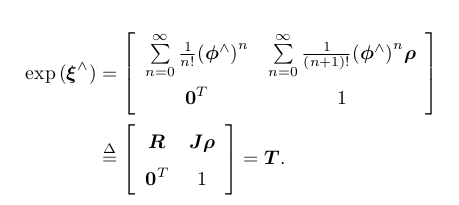
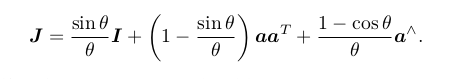
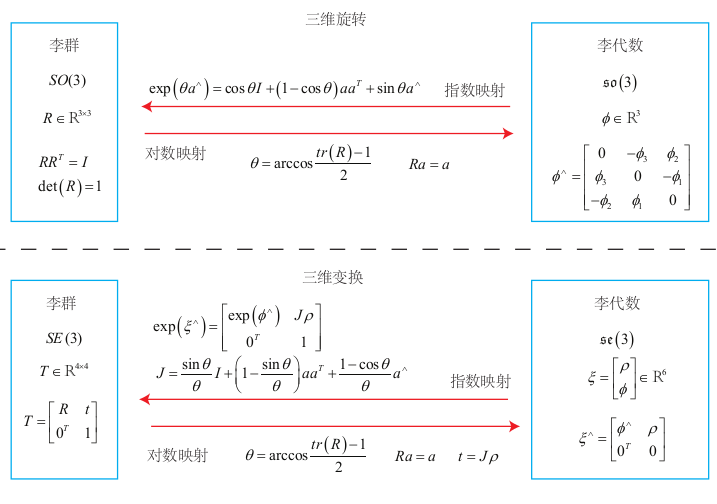
SO(3), SE(3), so(3), se(3) 的对应关系:
李代数求导与扰动模型
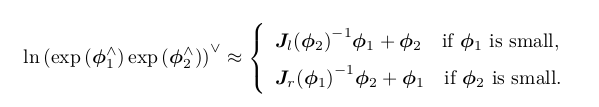
该式告诉我们,当对一个旋转矩阵 R 2 (李代数为 φ2 )左乘一个微小旋转矩阵 R 1 (李代数为 φ 1 )时,可以近似地看作,在原有的李代数 φ 2 上,加上了一项 J l (φ 2 )−1φ 1 。同理,第二个近似描述了右乘一个微小位移的情况。于是,李代数在 BCH近似下,分成了左乘近似和右乘近似两种,在使用时我们须加注意,使用的是左乘模型还是右乘模型。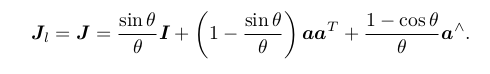
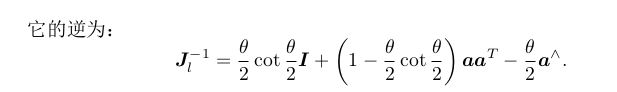
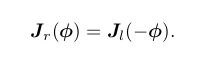
假定对某个旋转 R,对应的李代数为 φ。我们给它左乘一个微小旋转,记作 ∆R,对
应的李代数为 ∆φ。那么,在李群上,得到的结果就是 ∆R · R,而在李代数上,根据 BCH
近似,为:J l −1 (φ)∆φ + φ。合并起来,可以简单地写成:
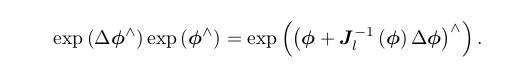
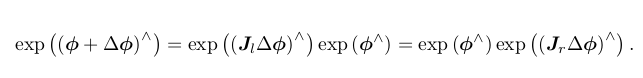
同样的,对于 SE(3),亦有类似的BCH 近似公式:
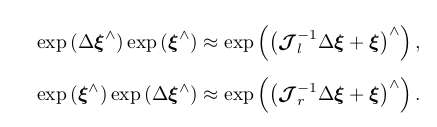
李代数求导:
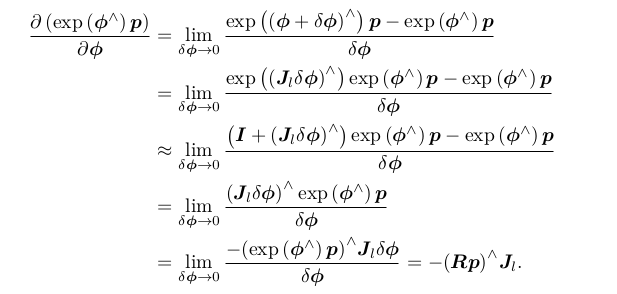
扰动模型(左乘)求导:
我们以左扰动为例。设左扰动 ∆R 对应的李代数为φ。然后,对 φ 求导,即:
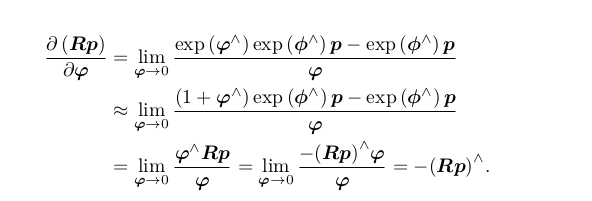
优点:不用计算Jl
SE(3) 上的李代数求导:
假设某空间点 p 经过一次变换 T (对应李代数为 ξ),得到 T p ¬ 。现在,给 T 左乘一个扰动
∆T = exp (δξ ∧ ),我们设扰动项的李代数为 δξ = [δρ, δφ] T ,那么: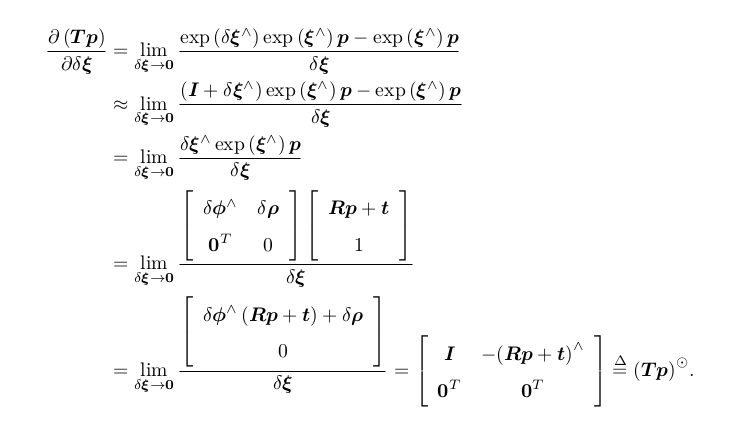



 浙公网安备 33010602011771号
浙公网安备 33010602011771号