机器学习-Logistic回归

Logistic回归

假设陈述

 　　

　　是最通用的二分分类算法。识别一张图片，结果对则1，否则0.

　　若图是64X64像素，有三个矩阵分别为图的红绿蓝像素表示，将之合成一个特征向量则为64X64X3=12288大小。

　　用n_x=12288来表示输入的特征向量x的维度。要输出预测结果y。

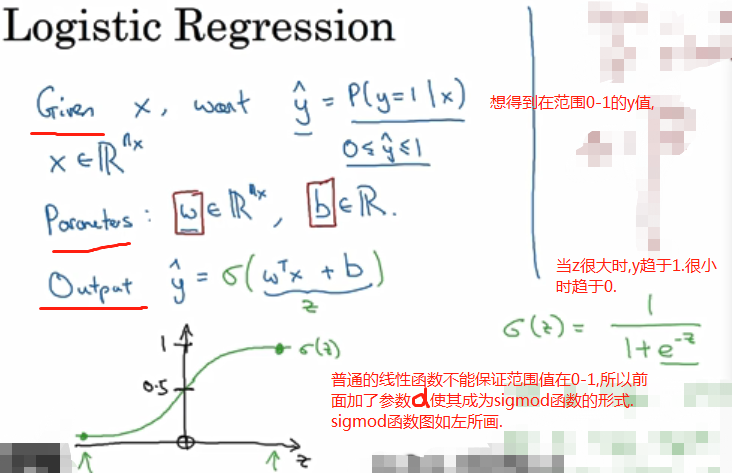　　要训练w和b。

决策界限

　　

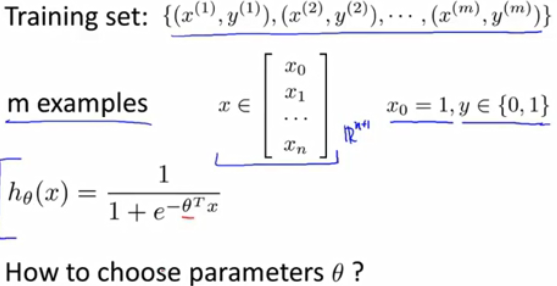
代价函数

　　   

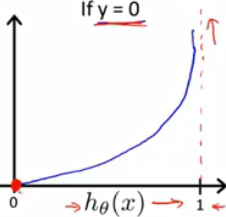
　　普通的平方误差函数在以后的优化中可能是一个非凸函数，即有好多局部最优解，歪歪扭扭，为了得到凸函数使函数更平滑，会用其他代价函数：（注意损失函数是在单个样本上定义的，测试单个样本训练结果；成本函数用于衡量w和b的效果）

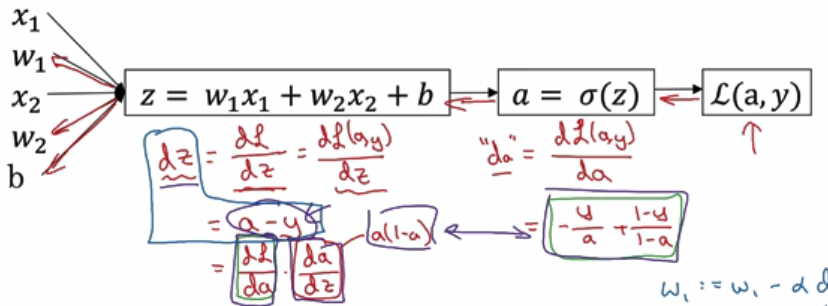
Logistic回归的梯度下降法

　　梯度下降法：学习训练集上的w，b

 　　  

　　

　　

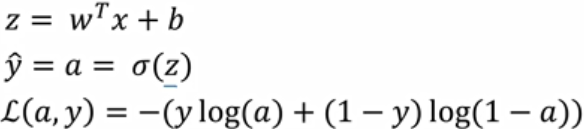
　　求导后算式如下：

 

　　同理，对d也是重复计算类似过程。

　　微积分中，若有多个变量求导，则用偏导数符号α表示，只有一个变量，导数用d表示。

　　适用于梯度下降的特征缩放也适用于logistic回归。

　　 

　　M个样本的梯度下降

 　　

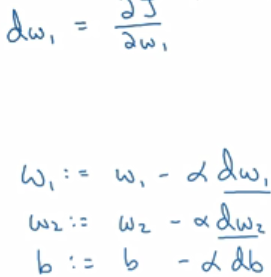
向量化：

   　　　　　　  

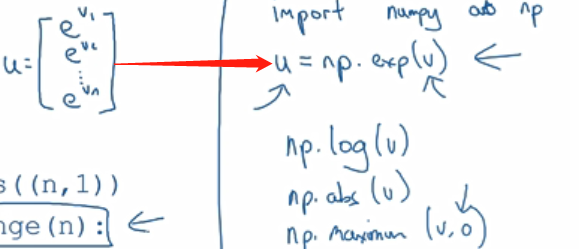
　　向量化方法快了几百倍。尽量避免用for，先看是否能用numpy库中的内置函数。

　　将向量化应用到logistic回归梯度下降算法实现：

　　 　　

 　　　　

 　　　　

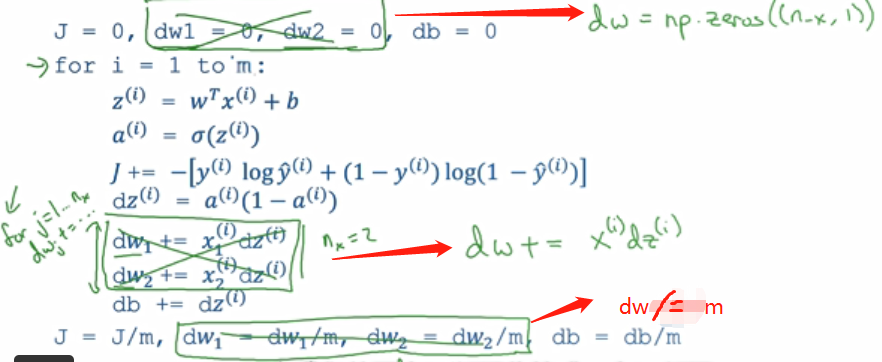
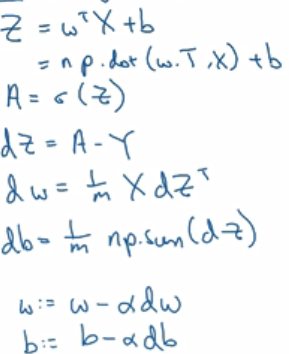
高级优化

　　是回归速度更快，比梯度下降更好。

　　 

　　

 

　　代码：

　　Cmd运行：

　　 

 　　

 　　

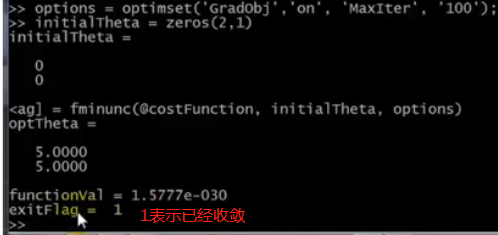
　　注意：θ维度必须〉=2

　　 

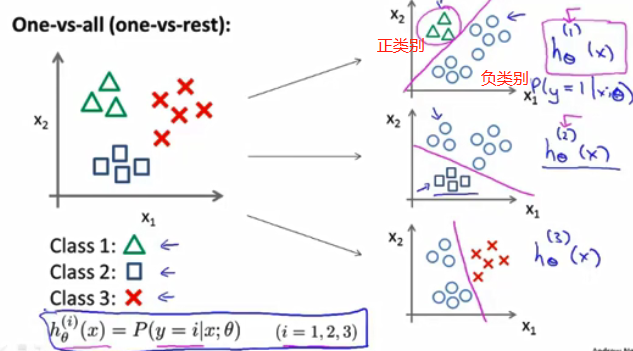
多元分类：一对多

　　一对多分类，有时也称为一对余。