机器学习-线性回归（单变量，多变量）

单变量线性回归

模型描述

 　　

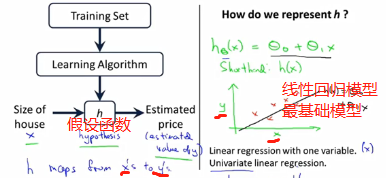
代价函数。

　　即讨论如何选择预测函数中的参数θ0和θ1，使得函数与实际数据点尽量好的拟合。使平方差尽量小。

　　m指训练集的样本容量。改变θ0和θ1求代价函数J（θ0，θ1）函数的最小值。也叫平方误差函数或平方误差代价函数。

　　

　　若只有一个参数得到的代价函数是一个碗状图。两个参数得到的是三维空间的碗状图，一般用等高线图表示，即下图第二图。

　　             

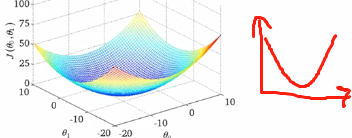
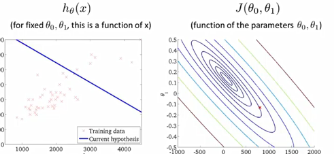
　　中心是最小值点。

梯度下降

　　一种可以自动找到使函数J最小的θ0，θ1算法。使函数最小化，不止适用于线性函数。

　　 

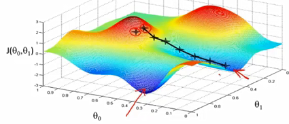
　　原理：选中一点，环顾360度，找到最快下山的那个方向点，迈一步，不断重复，直到找到最低点或局部最低点。

　　特点：若从不同点出发下山，很可能会得到不同的局部最优解。

　　数学原理：

　　α表示学习率，即每次要迈多大的步子。当接近局部最低点时，梯度函数会自动逐渐缩小步伐。

　　：=在计算机中是赋值操作，=是判断是否等于。

　　θ0，θ1是同步更新，注意下图四个步骤地顺序。

 　　

线性回归的梯度下降算法

 　　　

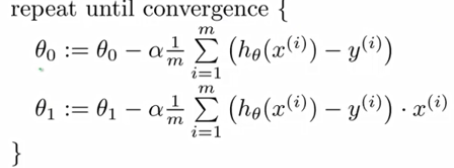
　　只有全局最优。也叫Batch梯度下降：每一步梯度下降都遍历了整个训练集样本。

　　高数上有正规方程组方法可以求出代价函数最小值。不过梯度下降算法适用于大的数据集。

线性代数回顾

　　4x3的矩阵指某一个矩阵。R^4x3指所有4x3矩阵的集合。大写字母表示矩阵，小写表示数字。

　　向量是只有一列的矩阵，n维向量。R⁴指所有4维向量的集合

 　　

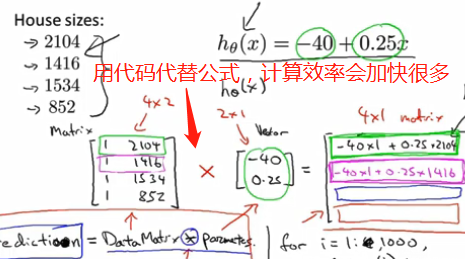
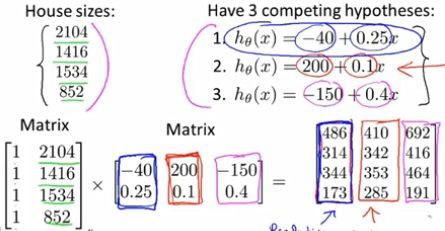
　　矩阵相乘可以用来解决线性回归问题中参数θ0和θ1的计算问题。而不需要梯度下降算法等迭代算法。矩阵乘法不可交换，可组合律。单位矩阵Inxn

 　　

　　逆矩阵：两者相乘=单位矩阵。 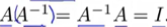方阵才有逆矩阵。

　　　　Condave软件的pinv（A），好多软件也有公式直接求逆矩阵。

　　　　不存在逆矩阵的矩阵可以理解为奇异矩阵或退化矩阵。

　　矩阵转置：i行变第i列。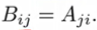

多变量线性回归

多功能

　　    

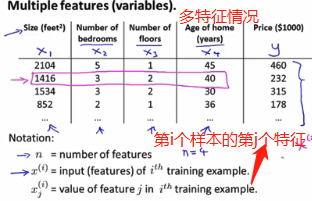
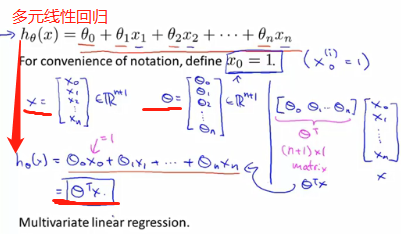
多元梯度下降法

　 　　　　　       

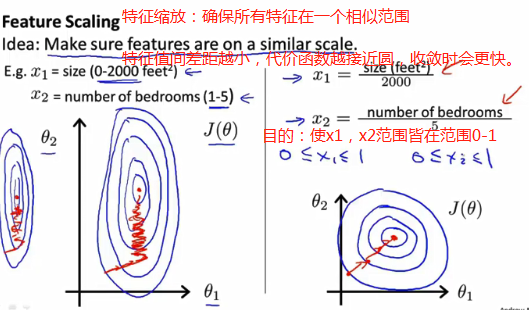
　　使梯度下降算法使用技巧一：均值归一化，使收敛加快。

 　　

　　使梯度下降算法使用技巧二：学习率α，算法更新规则之一。以确保梯度下降正常工作。

　　希望找到一个θ能最小化代价函数J(θ)。但若下图曲线是往上或者上下浮动，说明学习率太大，越过最低点了，要尽量使学习率低点。

 　　

特征和多项式回归

　　有时通过定义新特征会得到更好的模型。例：预测房价，有两个参数，房子长与深度，若认为一个特征x = 房子长*房子深，可以决定房子价格，则最终可以认为h（θ）=θ₀+θ₁x。

 　　

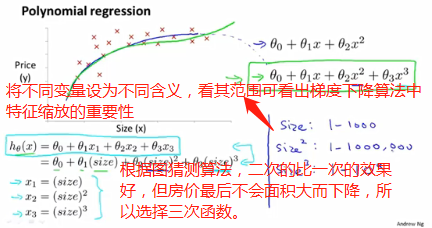
　　上图除了三次函数还有其他选择：

　　要学会寻找特征，函数的多选择性。

正规方程

 　　

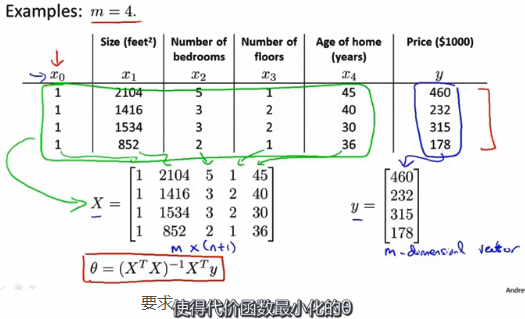
　　上图方程若是遇到不可逆矩阵怎么办？计算机有两个计算逆的方法：pinv和inv，pinv即使处理非可逆矩阵，也会出来结果，称为伪逆。两者区别，是进阶知识。

　　若矩阵是奇异矩阵或不可逆，则先看特征里面是否有多余的特征，若多余则删除；再看是否有过多的特征，可以删不必要的特征或使用正规化。

 　　

　　交作业流程：

　　先看pdf文件，明确要求并编写代码。再在Octave中运行，

　　代码：A = eye（5）；输出一个标准矩阵。