62(持续更新中)

概念

生成树：对于一个无向连通图，边带有权，求具有全部n个定点，n-1条边的连通子图，这一个子图就是生成树。

最小生成树：在所有的子图中，边的权值之和最小的哪一个子图。

算法

Kruskal算法

定理：

在一个无向连通边带权图中，任意一个最小生成树必定包含边的权值最小的哪一个边。

如果不包含，连上这一条边，去掉环上的另一条边，最终得到的权值会更优。假设不成立，原命题成立。

kruskal中，由于定理成立，所以一定包含最小权值的哪一个边，由《离散数学》知：树中不能有环。所以已经连接成的点一定不能在内部再连接了。这个时候，可以把已经连接的一个块看成一个点（如果是块中的不同点，由于已经连接，所以不同点也是相连的。所以可以把连接在这一个块上的所有边都看做是连在块上），再进行最小生成树算法重复之前的步骤（选一个最小的边....）

程序实现：

在实际的程序中，并不需要进行缩点。而是把边进行排序，从小到大进行试，如果是已经连接在一起的点，那么就忽略，否则选择这一条边。

算法的时间复杂度：\(O(mlog_2m)\)

#include <bits/stdc++.h>
using namespace std;
#define N 310
#define M 505
int fa[N];
struct edge{
    int x, y, z;
}a[M];
bool operator < (const edge & u, const edge &v) {
    return u.z < v.z;
}
int get(int x)
{
    if(x == fa[x]) return x;
    else return fa[x] = get(fa[x]);
}
int main()
{
    int ans = 0;
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++)
    {
        scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].z);
    }
    sort(a+1, a+1+m);
    for(int i = 1; i <= n; i++) fa[i] = i;
    for(int i = 1; i <= m; i++)
    {
        int x = get(a[i].x);
        int y = get(a[i].y);
        if(x == y) continue;
        ans += a[i].z;
        fa[x] = y;
    }
    printf("%d", ans);
    return 0;
}

prim算法

严格证明：

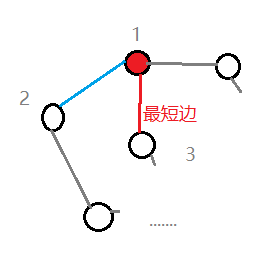
从某一个点出发，有许多边可以进行选择。一定要选择最小的边。

如果不选择最小的边：

假设选择了除了红色边以外的，与1邻接的边。那么到了最后，所有都会连通。假设从1到3经过蓝色边，那么连接红色边，成为一个环，然后去除蓝色边，达到最优的结果。

故假设不成立，原命题成立！

如果在开始不选红色边，到最后可能阴差阳错地选了红色边，这时候答案仍然是最优，但是很离谱。

所以应该选择权值最小的边。

之后，由于：

1. 已经连接的不能再连接（由树的定义不能有环）
2. 块里面的任意两个点是连通的

所以进行缩点，然后再重复进行求解。

#include <bits/stdc++.h>
using namespace std;
#define N 305
int a[N][N];
int d[N];
bool v[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    memset(a, 0x3f, sizeof(a));
    //for(int i = 1; i <= n; i++) a[i][i] = 0;这一句话其实没有什么用
    for(int i = 1; i <= m; i++)
    {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        a[x][y] = a[y][x] = min(z, a[y][x]);
    }
    memset(d, 0x3f,sizeof(d));
    memset(v, 0, sizeof(v));
    d[1] = 0;
    for(int i = 1; i <= n-1; i++)
    {
        int x = 0;
        for(int j = 1; j <= n; j++)
            if(!v[j] && (x == 0 || d[j] < d[x])) x = j;
        v[x] = 1;
        for(int y = 1; y <= n; y++)
        {
            if(!v[y] && d[y] > a[x][y]) d[y] = a[x][y];
        }
    }
    int ans = 0;
    for(int i = 1; i <= n; i++) ans += d[i];
    printf("%d\n", ans);
    return 0;
}

解释：由于在没有被选择之前，d值会被更新，但是在选择之后，d值保持不变。所以到最后，d里面存的就是这一个点被选中的会后的d（代价）

在这里所使用的图的存储方法是邻接表，时间复杂度是\(n^2\).

两种方法的选择

如果是稠密图，那么就选择prim算法。

如果是稀疏图，那么就选择kruskal算法。

AcWing346. 走廊泼水节

给定一棵 N 个节点的树，要求增加若干条边，把这棵树扩充为完全图，并满足图的唯一最小生成树仍然是这棵树。

求增加的边的权值总和最小是多少。

注意： 树中的所有边权均为整数，且新加的所有边权也必须为整数。

输入格式

第一行包含整数 t，表示共有 t 组测试数据。

对于每组测试数据，第一行包含整数 N。

接下来 N−1 行，每行三个整数 X,Y,Z，表示 X 节点与 Y 节点之间存在一条边，长度为 Z。

输出格式

每组数据输出一个整数，表示权值总和最小值。每个结果占一行。

数据范围

1≤N≤6000

1≤Z≤100

输入样例：

2
3
1 2 2
1 3 3
4
1 2 3
2 3 4
3 4 5 

输出样例：

4
17 

在这一道题目中有两种方法：

方法一：根据点进行考虑（\(O(n^3)\)）

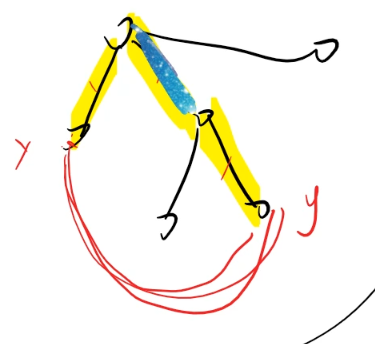
如图，除了红色边以外，其余部分就是最初的那一棵树。如果红色的边比从x到y的线段中的一条小，那么就可以把某一条去掉，加上红色边。

所以任意两点之间的边的权值一定大于这生成树中这两个点之间的路径上的最大边。

不妨取最大边的权值+1.

如果是这样的话，那么由最后的完全图所得到的生成树中有一个就是最初的树。如果进行替换，那么结果一定不是最优。所以原来这一棵树就时唯一的最小生成树。

具体实现需要枚举每一个点，同时对树进行一次遍历。

总共的时间复杂度是（\(O(n^3)\)）。

方法二：考虑使用kruskal算法。

把生成树的边进行从小到大排序。这也就是完全图得到生成树所拓展的边。

当有两个集合，两个集合中两两都有边相连。那么把这两个集合合并之后，并且把这两个集合中的$ \forall x\in A, \forall y\in B$，x与y之间添加一条边。那么这一个集合也是两两之间有边的。

对于枚举到的边（x, y, z），左右是两个集合，那么这两个集合之间连边，边的长度就取z+1.

#include <bits/stdc++.h>
using namespace std;
#define N 6005
int fa[N], sz[N];
struct edge{int x, y, z;}a[N];
inline bool operator < (const edge &x, const edge &y)
{
    return x.z < y.z;
}
int get(int x)
{
    if(x == fa[x]) return x;
    return fa[x] = get(fa[x]);
}
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        int ans = 0;
        int n;
        scanf("%d", &n);
        for(int i = 1; i <= n-1; i++)
        {
            scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].z);
        }
        sort(a+1, a+n);
        for(int i = 1; i <= n; i++) fa[i] = i, sz[i] = 1;
        for(int i = 1; i <= n-1; i++)
        {
            int x = get(a[i].x);
            int y = get(a[i].y);
            fa[x] = y;
            ans += (sz[x]*sz[y]-1) * (a[i].z+1);
            sz[y] += sz[x];
        }
        printf("%d\n", ans);
    }
    return 0;
}

AcWing347. 野餐规划

一群小丑演员，以其出色的柔术表演，可以无限量的钻进同一辆汽车中，而闻名世界。

现在他们想要去公园玩耍，但是他们的经费非常紧缺。

他们将乘车前往公园，为了减少花费，他们决定选择一种合理的乘车方式，可以使得他们去往公园需要的所有汽车行驶的总公里数最少。

为此，他们愿意通过很多人挤在同一辆车的方式，来减少汽车行驶的总花销。

由此，他们可以很多人驾车到某一个兄弟的家里，然后所有人都钻进一辆车里，再继续前进。

公园的停车场能停放的车的数量有限，而且因为公园有入场费，所以一旦一辆车子进入到公园内，就必须停在那里，不能再去接其他人。

现在请你想出一种方法，可以使得他们全都到达公园的情况下，所有汽车行驶的总路程最少。

输入格式

第一行包含整数 n，表示人和人之间或人和公园之间的道路的总数量。

接下来 n 行，每行包含两个字符串 A、B 和一个整数 L，用以描述人 A 和人 B 之前存在道路，路长为 L，或者描述某人和公园之间存在道路，路长为 L。

道路都是双向的，并且人数不超过 20，表示人的名字的字符串长度不超过 10，公园用 Park 表示。

再接下来一行，包含整数 s，表示公园的最大停车数量。

你可以假设每个人的家都有一条通往公园的道路。

输出格式

输出 Total miles driven: xxx，其中 XXX 表示所有汽车行驶的总路程。

输入样例：

10
Alphonzo Bernardo 32
Alphonzo Park 57
Alphonzo Eduardo 43
Bernardo Park 19
Bernardo Clemenzi 82
Clemenzi Park 65
Clemenzi Herb 90
Clemenzi Eduardo 109
Park Herb 24
Herb Eduardo 79
3

输出样例：

Total miles driven: 183

方法一

这道题目里面重点是要把开车的总路程和一条隐形的路进行关联。

在这里，我们忽略具体是那一辆车出发，只关心最终车走的轨迹。

由题意知道，所有的小丑必须到达广场，这意味中每一个点在汽车轨迹的引导下都是连通的。

要让所有的汽车走过的路最少，由此想到了最小生成树的做法。

但是 公园的停车场能停放的车的数量有限 并且 所以一旦一辆车子进入到公园内，就必须停在那里（这个是防止把车子开进去再开出来，再把其他车子开进去这类神仙操作）

park的 度 需要进行控制。

1. 最小生成树的park点的入度小于等于s，则可行。
2. 如果大于s，那么就需要删去这一条边，把割出去的连通块与除了park的其他点进行连接。
   
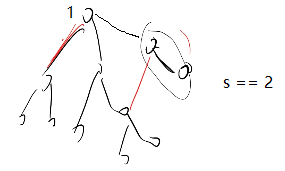
   这时候需要删除一条边。可能删除三个中的任意一条。这时候应该枚举这三条边，然后找到把连通块与除park以外的点相连的最短路径。把三个路径长度取最小值，选择这一种方案。
   如果s==1，那么就删除两次。每一次删除都是取得最小值。
   证明：如果到最后还没有选取最小值，那么可以通过这一种方案进行替换，使得结果更优。

#include <bits/stdc++.h>
using namespace std;
#define N 50
int m, n, s;//n表示点数，m表示边数，s表示停车场最大允许的车辆
int a[N][N], b[N][N];//a是原来的图。b是生成树的图
int v[N];
int ans = 0;
int deg;//1号点的度
void read()
{
    static map<string, int >mp;
    n = 1, mp["Park"] = 1;//注意P是大写
    scanf("%d", &m);
    memset(a, 0x3f, sizeof(a));
    for(int i = 1; i <= m; i++)
    {
        char sx[12], sy[12];
        int z;
        scanf("%s%s%d", sx, sy, &z);
        if(mp[sx] == 0) mp[sx] = ++n;
        if(mp[sy] == 0) mp[sy] = ++n;
        int x = mp[sx], y = mp[sy];
        a[x][y] = a[y][x] = min(z, a[x][y]);
    }
    scanf("%d", &s);
    //for(auto x : mp) cout << x.first << "  " << x.second << endl;
}
void prim()
{
    static int d[N];
    static int conn[N];//保留信息，以构建生成树（表示与x相连的点是conn[x]）
    memset(v, 0, sizeof(v));
    memset(d, 0x3f, sizeof(d));
    d[1] = 0;
    for(int i = 1; i <= n-1; i++)
    {
        int x = 0;
        for(int j = 1; j <= n; j++)
            if(!v[j] && (x == 0 || d[j] < d[x])) x = j;
        v[x] = 1;
        for(int y = 1; y <= n; y++) 
            if(!v[y] && (d[y] > a[x][y])) d[y] = a[x][y], conn[y] = x;
    }
    for(int i = 1; i <= n; i++) ans += d[i];
    memset(b, 0x3f, sizeof(b));
    for(int i = 2; i <= n; i++)
    {
        int x = conn[i], y = i;
        b[x][y] = b[y][x] = d[i];
        if(x == 1) deg++;
    }
}
void dfs(int x)//找到连通块
{
    if(v[x]) return;
    v[x] = 1;
    for(int i = 2; i <= n; i++) if(b[i][x] < 0x3f3f3f3f)
        dfs(i);
}
void solve()
{
    int min_val = 0x3f3f3f3f;
    int mx = 0, my = 0, mini = 0;//注意要有着三个值。
    for(int k = 2; k <= n; k++) if(b[k][1]<0x3f3f3f3f)//注意不要写的重复了。我最一开始这个也是使用i进行循环
    {
        memset(v, 0, sizeof(v));
        v[1] = 1;//强制不让拜访
        dfs(k);
        for(int i = 2; i <= n; i++) if(!v[i])
            for(int j = 2; j <= n; j++) if(v[j])
            {
                if(a[i][j]-b[1][k] < min_val)
                {
                    min_val = a[i][j]-b[1][k];
                    mx = i, my = j, mini = k;
                }
            }
    }
    ans += min_val;
    b[mx][my] = b[my][mx] = a[mx][my];//不是b[mx][my] = a[mx][my];
    b[1][mini] = b[mini][1] = 0x3f3f3f3f;
    deg --;
}
int main()
{
    read();
    /*
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)
            printf("%d  ", a[i][j]);
        puts("");
    }
    */
    //cout << n;
    prim();
    while(deg > s) 
        solve();
    printf("Total miles driven: %d", ans);
    return 0;
}

一定要整理好思路，然后写代码，否则DEBUG很辛苦。

方法二