KNN算法详解

    简单的说，K近邻算法是采用不同特征值之间的距离方法进行分类。

   该方法优点：精确值高、对异常值不敏感、无数据输入假定

   缺点：计算复杂度高、空间复杂度高

   适用范围：数据型和标称型

   现在我们来讲KNN算法的工作原理：存在一个样本数据集，也称作训练样本集，并且样本中每条数据都存在标签。将新输入的没有标签的数据与训练样本数据集中每条数据进行距离计算，选择前K个最小距离。并统计出现次数最多的分类。将该分类作为新数据的标签。

  例如：使用k-近邻算法分类爱情片和动作片。

            训练样本数据集如下：

            

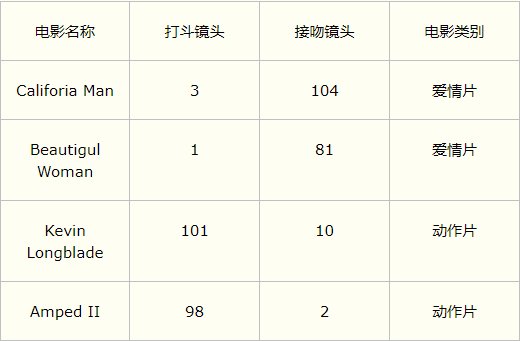
           此时给定一部电影的统计数据：打斗镜头：18，接吻镜头：90，判断该电影属于哪种类型？

          分别计算该条数据与样本集中各条数据的距离：

          

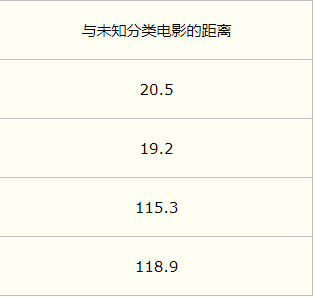
         假设K=3，将距离从小到大排列，选择前三条数据，并统计出该三条数据中所属类别最多的类别。并将该类别赋值给新输入数据。如上所属，该输入数据的类别为爱情片。

        K-近邻算法的一般流程：

       （1）收集数据

       （2）准备数据：距离计算所需的数值，最好是结构欧化数据格式

       （3）分析数据

       （4）训练数据：此步骤不适用与K-近邻算法

       （5）测试数据：计算错误率

       （6）使用数据：首先需要输入样本数据和结构化数据的输出结果，然后运用K近邻算法判断输入数据分别属于哪一类，最后应用对计算出的分类执行后续处理

        实现代码如下：

       

import numpy as np
import operator
from os import listdir

def createDateSet():
    group=np.array([[1,1.1],[1,1],[0,0],[0,0.1]])
    labels=['A','A','B','B']
    return group,labels
#分类
def classify(inX,dataSet,labels,k):
    dataSetSize=dataSet.shape[0]
    diffMat=np.tile(inX,(dataSetSize,1))-dataSet
    sqDiffMat=diffMat**2
    sqDistances=sqDiffMat.sum(axis=1)
    distances=sqDistances**0.5
    ##argsort()根据元素的值从大到小对元素进行排序，返回下标
    sortedDistance=distances.argsort()
    classCount={}
    for i in range(k):
        voteIlabel=labels[sortedDistance[i]]
        classCount[voteIlabel]=classCount.get(voteIlabel,0)+1
    sortedClassCount=np.sort(classCount.items(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]
#获取数据
def filematrix(filename):
    fr=open(filename)
    arrayLine=fr.readlines()
    numberOfLines=len(arrayLine)
    returnMat=np.zeros((numberOfLines,3))
    classLabelVector=[]
    index=0
    for line in arrayLine:
        line=line.strip().split('\t')
        returnMat[index,:]=line[0:3]
        classLabelVector.append(int(line[-1]))
        index+=1
    return returnMat,classLabelVector
#归一化数据
def autoNorm(dataSet):
    minVals=dataSet.min(0) #0表示列
    maxVals=dataSet.max(0)
    ranges=maxVals-minVals
    normDataSet=np.zeros(np.shape(dataSet))
    m=dataSet.shape[0]
    normDataSet=dataSet-np.tile(minVals,(m,1))
    normDataSet=normDataSet/np.tile(ranges,(m,1))
    return normDataSet,ranges,minVals

def datingClassTest():
    hoRatio=0.10
    datingDataMat,datingLabels=filematrix('../data/testSet.txt')
    normMat,rangs,minVals=autoNorm(datingDataMat)
    m=normMat.shape[0]
    numTestVecs=int(m*hoRatio)
    errorCount=0.0
    for i in range(numTestVecs):
        classifierResult=classify(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
        print("预测类别为：",classifierResult,"实际类别：",datingLabels[i])
        if(classifierResult!=datingLabels[i]):
            errorCount+=1
    print("总的错误率：",(errorCount/float(numTestVecs)))

def img2vector(filename):
    returnVect=np.zeros((1,1024))
    fr=open(filename)
    for i in range(32):
        lineStr=fr.readlines()
        for j in range(32):
            returnVect[0,32*i+j]=int(lineStr[j])
    return returnVect

def handwritingClassTest():
    hwLabels = []
    trainingFileList = listdir('trainingDigits')           #load the training set
    m = len(trainingFileList)
    trainingMat = np.zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        hwLabels.append(classNumStr)
        trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
    testFileList = listdir('testDigits')        #iterate through the test set
    errorCount = 0.0
    mTest = len(testFileList)
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
        classifierResult = classify(vectorUnderTest, trainingMat, hwLabels, 3)
        print ("the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr))
        if (classifierResult != classNumStr): errorCount += 1.0
    print ("\nthe total number of errors is: %d" % errorCount)
    print ("\nthe total error rate is: %f" % (errorCount/float(mTest)))