树的遍历 Shaass the Great : CodeForces294E
题目:CodeForces - 294E
题意:
有一棵树,切断某条边之后,重造一条长度一样的边连接两个新子树,使得新子树所有点到所有点的距离和最小。
思路:
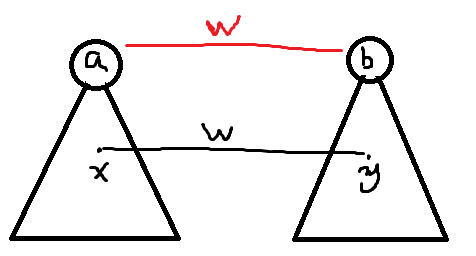
枚举切断的边,如图,红色为删除的边,这条被删除边的两个顶点不妨直接设为两颗新树的根节点.
x->y为期望添加的边,表示成黑色,长度相同.
假设新生成的子树为tree1和tree2。再将tree1中的x点连接到tree2的y点上,长度为w。记子树1中所有点到所有点的距离和为Sum1,子树2为Sum2。子树1中所有点到x点的距离和为Sx,子树2中所有点到y点的距离和为Sy。子树1的节点个数为size1,子树2的节点个数为size2。
则新子树的距离和为\(sum1+sum2+w*size1*size2+Sx*size2+Sy*size1\)
易知\(sum1+sum2+w*size1*size2\)为定值,这道题的关键是如何选取x和y使得Sx和Sy最小,而这两个又是独立的问题,我们拿其中之一讨论即可。
不妨直接将w路径上的左端点a作为子树1的根,我们可以通过DFS求出子树1中所有点的Sx,即在DFS的同时得出每个点u到根a的距离\(S_{u,a}\),以及该点u往下的节点个数\(size_u\),最后累加\(S_{u,a}\)即为Sa。即所有点到根节点a的距离和.
得到Sa后,相邻节点u的Su=Sa-\(W_{u,a}*size_u+W_{u,a}*(size_{tot}-size_u)\)。\(W_{u,a}\)为u到a的距离.即可算出子树1上所有点的Sx.
累加Sx即为Sum1,通过DFS就可以得到所有所需的变量值了,后面就是枚举求最小了.
代码:
别人写的短代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
#define forw(i,x) for(int i=fir[x];i;i=ne[i])
#define M 20001
#define N M
LL C[M];
int cnt=1,ne[M],fir[M],to[M],from[M];
int n;
LL f[N];
int S[N];
LL ans =1e18;
int x,y;
LL z;
void dfs(int x,int fa)
{
f[x]=0;S[x]=1;
forw(i,x)
{
int V=to[i];
if(V!=fa)
{
dfs(V,x);
S[x]+=S[V];
f[x]+=f[V]+C[i]*S[V];
}
}
}
void add(int x,int y,LL z)
{
to[++cnt]=y;C[cnt]=z;ne[cnt]=fir[x];fir[x]=cnt;from[cnt]=x;
}
void DFS(int x,int fa,LL &p,int sum)
{
p=min(p,f[x]);
forw(i,x)
{
int V=to[i];
if(V!=fa)
{
f[to[i]]=f[x]+C[i]*(sum-S[V]*2);
DFS(V,x,p,sum);
}
}
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
cin>>x>>y>>z;
add(x,y,z);
add(y,x,z);
}
for(int i=2;i<=cnt;i+=2)
{
int U=from[i];int V=to[i];
dfs(U,V);
dfs(V,U);
LL p1=1e18,p2=1e18;
DFS(U,V,p1,S[U]);DFS(V,U,p2,S[V]);
long long dance=0;
for(int j=1;j<=n;j++) dance+=f[j];
long long it;
it=dance+2*(S[U]*S[V]*C[i]+p1*S[V]+p2*S[U]);
ans=min(ans,it);
}
cout<<ans/2;
return 0;
}
#pragma GCC optimize(3)
#include<cstdio>
#include<algorithm>
#define M 20000
using namespace std;
long long f[6666],si[6666],g[6666],ans;
int a[M],c[M],fi[M],ne[M],la[M],n,x,y,z,tot;
void add(int x,int y,int z){
a[++tot]=y;c[tot]=z;
!fi[x]?fi[x]=tot:ne[la[x]]=tot;la[x]=tot;
}
void dfs(int x,int fa){
f[x]=0;si[x]=1;
for(int i=fi[x];i;i=ne[i])if(a[i]!=fa){
dfs(a[i],x);
si[x]+=si[a[i]];
f[x]+=si[a[i]]*c[i]+f[a[i]];
}
}
void find(int x,int fa,long long &p,int num){
p=min(p,f[x]);
// printf("f[%d]=%lld\n",x,f[x]);
for(int i=fi[x];i;i=ne[i])if(a[i]!=fa){
f[a[i]]=f[x]+(num-2*si[a[i]])*c[i];
find(a[i],x,p,num);
}
}
int main(){
scanf("%d",&n);
tot=1;
for(int i=1;i<=n-1;i++){
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
int i=0;ans=1e18;
while(i<=tot){
i+=2;
if(i>tot)break;
dfs(a[i],a[i^1]);
dfs(a[i^1],a[i]);
long long p1=1e18,p2=1e18;
find(a[i],a[i^1],p1,si[a[i]]);
find(a[i^1],a[i],p2,si[a[i^1]]);
// printf("%d %d %lld %lld\n",a[i],a[i^1],p1,p2);
long long sum=0;
for(int j=1;j<=n;j++)sum+=f[j];
// printf("%lld\n",sum);
ans=min(ans,sum+2*(si[a[i]]*si[a[i^1]]*c[i]+p1*si[a[i^1]]+p2*si[a[i]]));
}
printf("%I64d",ans/2);
}
我自己写的长代码...
#include <bits/stdc++.h>
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
const int MAX_N = 5000 + 3;
struct Node {
int u,w;
bool f;//0输入的边 1反向边
};
vector<Node> tree[MAX_N];
int size[MAX_N],fa[MAX_N];
bool vis[MAX_N];
long long s[MAX_N];
int N,r1,r2,rt;
long long ANS,sum1,sum2,sx,sy;
void dfs(int u,long long sr)
{
size[u] = 1;
s[u] = sr;
vis[u]=true;
per(i,tree[u].size()-1,0) {
int v = tree[u][i].u;
int w = tree[u][i].w;
if (!vis[v]) {
dfs(v,sr+w);
size[u]+=size[v];
s[u] += s[v];
}
}
}
void dfs1(int u,long long& sum,long long& sx)
{
sum+=s[u];
sx = min(sx,s[u]);
vis[u]=true;
per(i,tree[u].size()-1,0) {
int v = tree[u][i].u;
int w = tree[u][i].w;
if (!vis[v]) {
s[v] = s[u] + (long long)w*(size[rt]-2*size[v]);
dfs1(v,sum,sx);
}
}
}
void task(int w)
{
memset(vis,0,sizeof(vis));
vis[r1]=vis[r2]=true;
fa[r1] = fa[r2] = 0;
dfs(r1,0);
dfs(r2,0);
rt=r1;
sum1 = sum2 =0;
sx = sy =0x7fffffffffffffff;
memset(vis,0,sizeof(vis));
vis[r1]=vis[r2]=true;
dfs1(r1,sum1,sx);
rt=r2;
dfs1(r2,sum2,sy);
long long tmp = (sum1>>1)+(sum2>>1)+sx*size[r2]+sy*size[r1]+(long long)w*size[r1]*size[r2];
ANS = min(ANS,tmp);
}
int main()
{
scanf("%d",&N);
rep(i,1,N-1) {
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
Node tmp;
tmp.u = b;
tmp.w = w;
tmp.f = false;
tree[a].push_back(tmp);
tmp.u = a;
tmp.f = true;
tree[b].push_back(tmp);
}
ANS=0x7fffffffffffffff;
rep(i,1,N) {
for(int j=tree[i].size()-1; j>=0; --j) {
Node tmp = tree[i][j];
if (!tmp.f) {
r1 = i;
r2 = tmp.u;
task(tmp.w);
}
}
}
printf("%lld",ANS);
return 0;
}
附上一个裸的求树的重心代码:(和本题关系不大,求树的重心代码本质也是同样的树的遍历)
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
using namespace std;
const int N = 50005;
const int INF = 1<<30;
int head[N];
int son[N];
bool vis[N];
int cnt,n;
int num,size;
int ans[N];
struct Edge
{
int to;
int next;
};
Edge edge[2*N];
void Init()
{
cnt = 0;
num = 0;
size = INF;
memset(vis,0,sizeof(vis));
memset(head,-1,sizeof(head));
}
void add(int u,int v)
{
edge[cnt].to = v;
edge[cnt].next = head[u];
head[u] = cnt++;
}
void dfs(int cur)
{
vis[cur] = 1;
son[cur] = 0;
int tmp = 0;
for(int i=head[cur];~i;i=edge[i].next)
{
int u = edge[i].to;
if(!vis[u])
{
dfs(u);
son[cur] += son[u] + 1;
tmp = max(tmp,son[u] + 1);
}
}
tmp = max(tmp,n-son[cur]-1);
if(tmp < size)
{
num = 1;
ans[0] = cur;
size = tmp;
}
else if(tmp == size)
{
ans[num++] = cur;
}
}
int main()
{
while(~scanf("%d",&n))
{
Init();
for(int i=1;i<=n-1;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
dfs(1);
sort(ans,ans+num);
for(int i=0;i<num;i++)
printf("%d ",ans[i]);
puts("");
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号