leetcode 834 树中距离之和

题目要求：求一个无向、连通的树状图中每个节点与其他节点的距离之和

输入：N = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]

输出：[8,12,6,10,10,10]

题解：

方法 1 ：

def solveI(N,edges):
    g=[[] for _ in range(N)]
    ans=[0]*N
    for i,j in edges:
        g[i].append(j)
        g[j].append(i)
    def dist(u):
        Sum=[0]*N
        Size=[1]*N
        def recur(cur, parent):
            for child in g[cur]:
                if child==parent: continue
                recur(child,cur)
                Sum[cur]+=Sum[child]+Size[child]
                Size[cur]+=Size[child]
        recur(u,-1)
        return Sum[u]
    return [dist(u) for u in range(N)]

Sum[i] 表示节点 i 到其子树中的每一个节点的距离之和，Size[i] 表示节点 i 和其子树的节点个数，有Sum[i] = ∑（Sum[child] + Size[child]），回溯结束可以发现根节点的Sum[root] 就是它与其他节点的距离之和。因此只要把各个节点都当作根节点进行 dfs，就能得到答案。

时间复杂度：O(n²)

方法 2 ：

方法1 复杂度高的原因在于每个节点都要被当作根节点进行 dfs，对大量的 Sum[i] 做了重复计算：如下图步骤 2 中所示：当 1 做根时，2、3、4的 Sum 都是没有变化的，只有 1 和其父节点 0 发生变化。

假设 p 为当前的根， c 是 p 的一个子节点，当 c 做根时 Sum 列表发生如下变化：（结合步骤 2 中的图形更好理解）

Sum[p] -= Sum[c] + Size[c]
Size[p] -= Size[c]
Sum[c] += Sum[p] + Size[p]
Size[c] += Size[p]

　　此时 Sum[c] 就是 c 节点与其他节点的距离之和，因此我们在 O(1) 时间内求出了一个解，将复杂度降为 O(N)+O(N) ~ O(N)。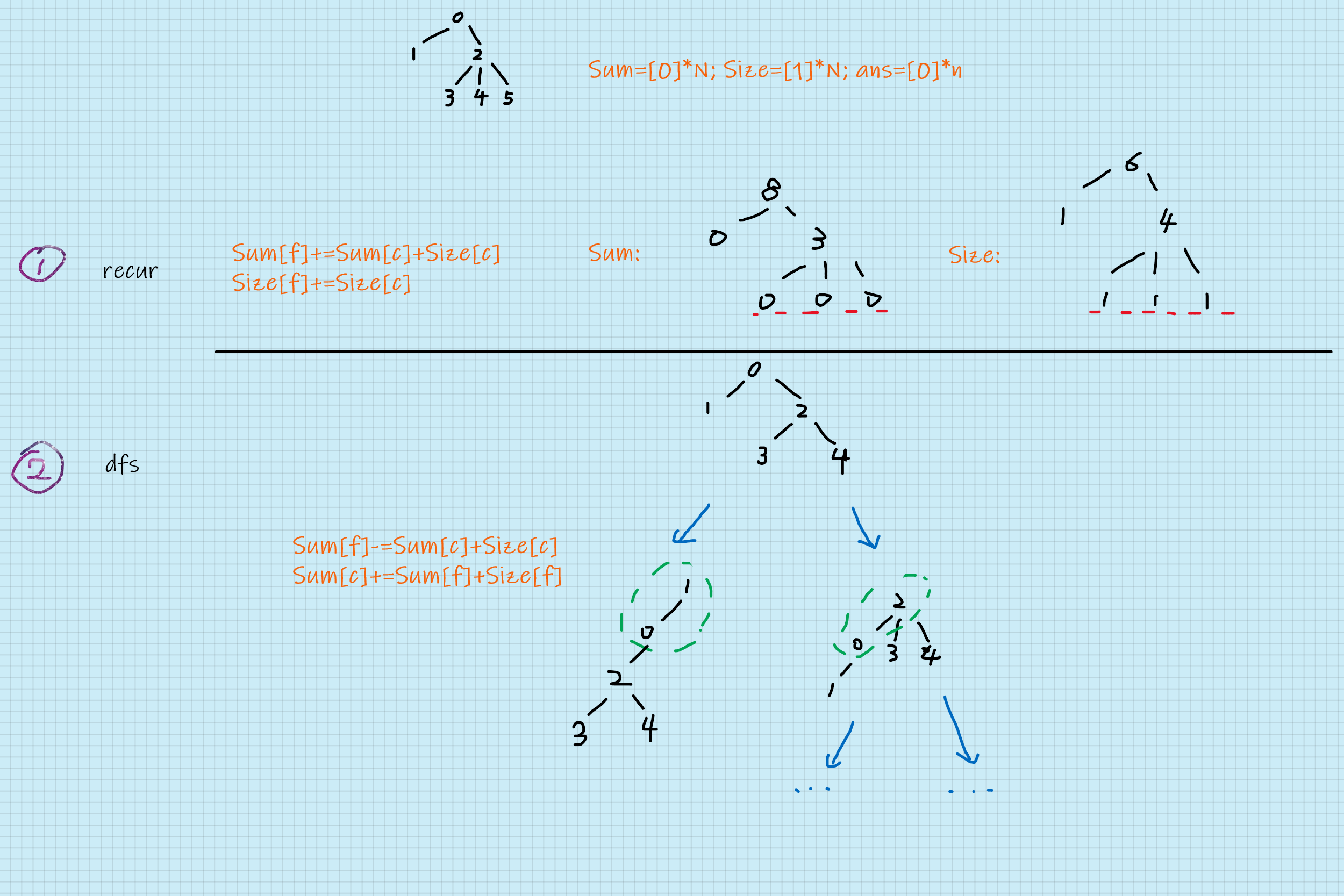

def solveII(N,edges):
    g=[[] for _ in range(N)]
    Sum=[0]*N
    Size=[1]*N
    ans=[0]*N
    for i,j in edges:
        g[i].append(j)
        g[j].append(i)
    def recur(cur, parent):
        for child in g[cur]:
            if child==parent: continue
            recur(child,cur)
            Sum[cur]+=Sum[child]+Size[child]
            Size[cur]+=Size[child]
    def dfs(cur, parent):
        ans[cur]=Sum[cur]
        Smc, Szc=Sum[cur], Size[cur]
        for child in g[cur]:
            if child==parent: continue
            Smch, Szch=Sum[child], Size[child]
            Sum[cur]-=Sum[child]+Size[child]    # modify tree
            Size[cur]-=Size[child]  # modify tree
            Sum[child]+=Sum[cur]+Size[cur]    # modify tree
            Size[child]+=Size[cur]  # modify tree
            dfs(child,cur)
            Sum[cur], Size[cur]=Smc, Szc    # switch back
            Sum[child], Size[child]=Smch, Szch  # switch back
    recur(0,-1)
    dfs(0,-1)
    return ans