背包问题（01背包，完全背包，多重背包（朴素算法&&二进制优化））
写在前面：我是一只蒟蒻~~~
今天我们要讲讲动态规划中最最最最最简单的背包问题
1. 首先，我们先介绍一下
01背包
大家先看一下这道01背包的问题
题目
有m件物品和一个容量为n的背包。第i件物品的大小是w[i]，价值是k[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。
题目分析：
我们刚刚看到这个题目时，有的人可能会第一想到贪心，但是经过实际操作后你会很~~神奇~~的发现，贪心并不能很好的解决这道题（没错，本蒟蒻就是这么错出来的）。这个时候就需要我们非常强大的动态规划（DP）出马。
我们可以看出，本题主要的一个特点就是关于物品的选与不选。这时候我们就会想如何去处理，才可以使我们装的物品价值总和最大，而且这道题的物品只有一个，要么选一个，要么不选。所以这个时候我们就可以推出它的状态转移方程（啥！你不知道啥是状态转移方程？那你自行理解吧）。
我们设f[i][j]为其状态。就有了以下式子
1 f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+k[i]);
i表示件数，j表示空间大小。
f[i][j]就表示i件物品下背包空间为j的状态。
f[i-1][j]表示在i-1件时背包空间为j的状态（在这中间则代表了在i件时不取这件物品）。
f[i-1][j-w[i]]+k[i]表示取这件物品后该背包的空间为j-w[i]，而总价值则增加了k[i]。
可能会有人问，这个式子跟我的贪心式子比有什么不一样的吗？
当然，这个式子能切掉这道题而贪心不行（这不是废话吗！！！）
嗯，说重点，这个式子只是牵扯到i-1件物品的问题，与其他无关，所以这就很好的解决了贪心对全局的影响。
可以显而易见的是其时间复杂度O（mn）（m是件数，n是枚举的空间）已经很优秀了，但是它的空间复杂度还是比较高，所以我们就可以使用一维数组进行优化，具体怎样优化，我们下面再说。
好了，说完这一题的核心码我们就可以得出f[m][n]所得到的是最优解。（为什么？？！！，如果你还不理解的话那我建议你上手动模拟一下，当然你也可以进入这里看一下是怎么操作的。
嗯，这道题就结束了，我们来一道确切存在的题目（洛谷）P1060 开心的金明
下面就是这道题的AC代码（如果你看懂了上面，代码就不难理解了）
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m; 4 int f[30][30007],w[30],v[30],k[30];//根据题目要求设置变量，f就表示状态 5 void dp(){ 6 memset(f,0,sizeof(f));//初始化（一般可忽略） 7 for(int i=1;i<=m;i++){//枚举物品数量 8 for(int j=w[i];j<=n;j++){//枚举背包空间 9 if(j>=w[i]){//如果背包空间能够装下下一件物品进行状态转移 10 f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+k[i]);//转移方程 11 } 12 } 13 } 14 } 15 int main(){ 16 scanf("%d%d",&n,&m); 17 for(int i=1;i<=m;i++){ 18 cin>>w[i]>>v[i]; 19 k[i]=w[i]*v[i];//读入+处理 20 } 21 dp();//进行处理 22 printf("%d",f[m][n]); 23 return 0; 24 }
这里对于01背包的讲解基本就结束了，下面给大家推荐几道题来练习，P1164 小A点菜 P1048 采药 P1049 装箱问题 。
最后，我来填一下我上面留下来的坑，如何优化二维01背包的空间复杂度。
很简单，就是把二维变为一维（啥！你说不明白？）这难道不是很显然的事情吗？你从f[i][j]变为f[i]直接缩小一维，空间不就小了一维吗。好了，下面，我们就谈谈如何实现的减维。
我们知道枚举从1~i来算出来f[i][j]的状态。所以，我们是不是可以用一个f[j]来表示每地i次循环结束后是f[i][j]的状态，而f[i][j]是由max(f[i-1][j],f[i-1][j-w[i]]+k[i])递推出来的，而我们只有从j=n到0的顺序进行枚举，这样才能保证推f[j]时f[j-w[i]]保存的是f[i-1][j-w[i]]的状态值。
核心代码
1 for(int i=1;i<=m;i++){ 2 for(int j=n;j>=w[i];j--){ 3 f[j]=max(f[j],f[j-w[i]]+k[i]); 4 } 5 }
这是一种比较好的写法，但还有的人（~~比如说我~~）就喜欢这样写（因为我很~~勤奋~~）
1 for(int i=1;i<=m;i++){ 2 for(int j=n;j>=0;j--){ 3 if(j>=w[i]){ 4 f[j]=max(f[j],f[j-w[i]]+k[i]); 5 } 6 } 7 }
这样我们都可以达到我们优化空间复杂度的目的（当然，我推荐大家写第一种，这样就不用担心判断大小的问题了）。
掌握这个优化其实十分重要的，有的题会卡二维数组的空间，这样我们只能用一维数组进行解题。
嗯，01背包就讲到这里了，希望能够帮到各位Oier，如有错误，请指出，本人定改正。
----手动分割一波=^ω^= ------
2、了解完01背包，我们来看一看
完全背包
老规矩，上题。
题目(P1616 疯狂的采药)：由于本蒟蒻~~比较懒~~，请大家点开自行看题。
下面进行题目分析：
我们不难看出，完全背包与01背包只是物品数量的不同，一个是只有1个，而物品的情况也只有 取和不取。但完全背包却是有无数多个，这就牵扯到一个物品取与不取和取多少的问题。这是的时间复杂度就不再是O（nm）了。而经过一些优化（这里给大家一个地址，大家可以在这里去看一看，本蒟蒻就不再展开讲解）
既然大家都已经明白了怎样进行优化（哪来的已经啊！！！假装假装吗≥﹏≤）
不管怎么说，我们就可以得到这个转移方程
1 f[j]=max(f[j],f[j-w[i]]+c[i]);
相信大家在理解01背包后，对完全背包的状态转移方程理解容易些。
其中的思想还是和01背包是相同的。
下面贴出AC代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 int T,n,v[10007],t[10007],f[100007];//变量的定义，f[]表示状态 4 5 int main(){ 6 scanf("%d%d",&T,&n);//读入 7 for(int i=1;i<=n;i++){ 8 cin>>t[i]>>v[i]; 9 } 10 memset(f,0,sizeof(f));//初始化（一般可忽略） 11 for(int i=1;i<=n;i++)//枚举物品i 12 { 13 for(int j=t[i];j<=T;j++){//背包空间（必须从t[i]开始，由于数量是无限的，所以，我们必须要递增枚举） 14 f[j]=max(f[j],f[j-t[i]]+v[i]);//状态转移 15 } 16 } 17 cout<<f[T];//输出答案 18 }
综上，就是完全背包的讲解，由于我懒，所以就不给大家推荐题了，我相信大家一定能够练习好的，嗯！我相信大家。（相信什么相信，快点干活！！（粉笔飞来）我闪 嗯，不存在的，正中靶心。
咳咳！我们来推荐最后一道题P2918 [USACO08NOV]买干草Buying Hay这一题希望大家好好想一想，有点坑，但是并不是太难，大家加油吧！！！！！
3、下一个，本蒟蒻不会！！！！
多重背包
等我学会，再来更新~~~~~
送给大家一个博客背包九讲
hello！我又回来了，今天我就来给大家来讲一讲我上回留下来的坑。
首先，我们先介绍一下何为多重背包。
问题描述：
多重背包：有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用，每件费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。
这里，我们可以看到多重背包与完全背包和01背包多不同的在于每件物品有有限多个，所以我们就产生了一种思路，那就是：将多重背包的物品拆分成01背包~~
这样一来，我们就可以用01背包的套路来解决这个问题，而这个代码呢，也很简单：
1 for(int i=1;i<=n;i++){ 2 for(int j=1;j<=num[i];j++){ 3 a[++cnt]=v[i]; 4 } 5 }
这样一来，我们就可以十分简单的解决这道题了！！！
但是，简单归简单，我们可以看到这个时间复杂度是十分不优秀的，所以我们可以想一想如何优化，
这时候我们来考虑一下进制的方法，
二进制
首先，我们先补充一个结论，就是1~n以内的数，都能够通过n进制以内的数组合得到。
这样的话，我们就可以通过二进制的拆分来进行优化，我们把每个物品有的所有个数，分开，
就比如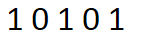
我们有这样一个数，
现在要进行二进制的拆分：
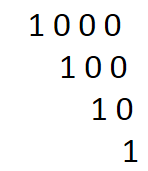
这时我们进行拆分之后发现还无法完全表示整个状态。。。所以我们就把这些都加起来：
（just like this）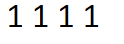
这样就OK了
核心代码：
1 for(int i=1;i<=6;i++){ 2 for(int j=1;j<=num[i];j<<=1){ 3 v[++cnt]=a[i]*j; 4 num[i]-=j; 5 } 6 if(num[i]>0)v[++cnt]=num[i]*a[i];//如果还有剩余，就全部加入 7 }
下面，我们来看一道例题：
题目描述：
POJ1742 Coins
- 总时间限制:
- 3000ms
- 内存限制:
- 65536kB
- 描述
- People in Silverland use coins.They have coins of value A1,A2,A3...An Silverland dollar.One day Tony opened his money-box and found there were some coins.He decided to buy a very nice watch in a nearby shop. He wanted to pay the exact price(without change) and he known the price would not more than m.But he didn't know the exact price of the watch.
You are to write a program which reads n,m,A1,A2,A3...An and C1,C2,C3...Cn corresponding to the number of Tony's coins of value A1,A2,A3...An then calculate how many prices(form 1 to m) Tony can pay use these coins. - 输入
- The input contains several test cases. The first line of each test case contains two integers n(1<=n<=100),m(m<=100000).The second line contains 2n integers, denoting A1,A2,A3...An,C1,C2,C3...Cn (1<=Ai<=100000,1<=Ci<=1000). The last test case is followed by two zeros.
- 输出
- For each test case output the answer on a single line.
- 样例输入
-
3 10 1 2 4 2 1 1 2 5 1 4 2 1 0 0
- 样例输出
-
8 4
这是什么意思呢？
我大概给大家翻译一下（原谅我蒟蒻的英语）
就是什么意思吧，给定N种硬币，其中第i种硬币的面值为Ai，共有Ci个。从中选出若干个硬币，把面值相加，若结果为S，则称“面值S能被拼成”。求1~M之间能被拼成的面值有多少个。
题目分析：
我们看到题目中给的是一个可行性的问题，我们只需要依次考虑每种硬币是否被用于拼成最终的面值，以“已经考虑过的物品种数”i作为dp的阶段，在阶段i时我们用f[i]表示前i种硬币能否拼成面值j。
法1：（朴素拆分发法）
代码：
1 bool f[100010]; 2 memset(f,0,sizeof(f)); 3 f[0]=1; 4 for(int i=1;i<=;i++){ 5 for(int j=1;j<=c[i];j++){ 6 for(int k=m;k>=a[i];k--){ 7 f[k]+=f[k-a[i]]; 8 } 9 } 10 } 11 int ans=0; 12 for(int i=1;i<=m;i++){ 13 ans+=f[i]; 14 } 15
这个题，这样解的话时间复杂度就太高，所以我们转换一个思路，来进行二进制拆分，
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define maxn 3004 4 int f[maxn][maxn],a[maxn],b[maxn],n; 5 6 int main(){ 7 scanf("%d",&n); 8 for(int i=1;i<=n;i++){ 9 scanf("%d",&a[i]); 10 }//读入 11 for(int i=1;i<=n;i++){ 12 scanf("%d",&b[i]); 13 } 14 for(int i=1;i<=n;i++){ 15 int val=0;//val代表f[i-1][j] 16 if(b[0]<a[i])val=f[i-1][0]; 17 for(int j=1;j<=n;j++){ 18 if(b[j]==a[i])f[i][j]=val+1; 19 else f[i][j]=f[i-1][j];//转移 20 if(b[j]<a[i])val=max(val,f[i-1][j]);//判断 21 } 22 } 23 int maxx=0; 24 for(int i=1;i<=n;i++){ 25 maxx=max(maxx,f[n][i]); 26 } 27 printf("%d\n",maxx); 28 29 return 0; 30 }
下面，我们来看一下另一道题：
划分大理石
题目描述：
描述
有价值分别为1..6的大理石各a[1..6]块，现要将它们分成两部分，使得两部分价值之和相等，问是否可以实现。其中大理石的总数不超过20000。
输入格式
有多组数据！
所以可能有多行
如果有0 0 0 0 0 0表示输入文件结束
其余的行为6个整数
输出格式
有多少行可行数据就有几行输出
如果划分成功，输出Can，否则Can't
样例输入
4 7 4 5 9 1 9 8 1 7 2 4 6 6 8 5 9 2 1 6 6 1 0 7 5 9 3 8 8 4 0 0 0 0 0 0
样例输出
Can't Can Can't Can't Can
看完这道题，我们不难看出，这是一道与P1164 小A点菜 十分相似的题，其中的不同点就是一个是01背包，一个是多重背包，所以我们就可以先用二进制进行拆分，然后再跑一遍DP即可。
代码：
#include<bits/stdc++.h> using namespace std; int num[7],a[7],dp[500007],v[100008],sum,cnt; int main(){ for(int i=1;i<=6;i++)a[i]=i; while(scanf("%d%d%d%d%d%d",&num[1],&num[2],&num[3],&num[4],&num[5],&num[6])){ if(!num[1]&&!num[2]&&!num[3]&&!num[4]&&!num[5]&&!num[6])break; sum=0; memset(v,0,sizeof(v)); memset(dp,0,sizeof(dp)); for(int i=1;i<=6;i++)sum+=(a[i]*num[i]); // printf("%d\n",sum); if(sum%2==1){ printf("Can't\n"); continue; } sum=sum/2; cnt=0; for(int i=1;i<=6;i++){ for(int j=1;j<=num[i];j<<=1){ v[++cnt]=a[i]*j; num[i]-=j; } if(num[i]>0)v[++cnt]=num[i]*a[i];//如果还有剩余，就全部加入 } dp[0]=1; for(int i=1;i<=cnt;i++){ for(int j=sum;j>=v[i];j--){ dp[j]+=dp[j-v[i]]; } } if(dp[sum])printf("Can\n"); else printf("Can't\n"); } return 0; }
2019.7.16
更新：单调队列优化多重背包
嗯，今天我们在课上学习了单调队列优化多重背包的方法（学的什么呀，都不会好吧），
首先，我们先来说一下，若使用单调队列来优化的话，时间复杂度可降至O(NM)，
首先，题面已经不再需要叙述了。
我们上一次的状态转移方程是将“阶段”这一维省略掉，
f[j]表示在前i种物品中选出若干放入到背包中体积之和为j的时候，价值的和的最大。
所以我们第一开始的状态转移的方程为：
F[i]=max1≤cnt≤Ci{F[j-cnt*vi]+cnt*Wi}
将决策换到一个数轴上表示每一个可能取值的点：如下图（从书上偷的（逃~））
当我们将j-1时得到的取值是这样的
这时，我们会发现对于j和j-1来说，转移之后所更新的内容并不快，因为两种的情况并没有重叠的部分。
我们现在考虑一下对于j和j-vi是什么情况
不难看出，这里的状态在更新时如果使用这样的更新的方式，速率会很快。
但是对于中间的这些数来说，就是相当于将j按照除以Vi的状态去分，对于每一组来说进行分别计算即可。
不难发现，这些分组的依据实现之后，我们得到的序列是单调的，这样的话我们就可以考虑来使用单调队列进行优化。
好了，今天就讲到这了。
后续背包推荐题目（ 持续更新……）：洛谷P1156（最优可将状态降至一维） ，洛谷P1417（背包加排序的组合） ，洛谷P5020 （经数学证明后，实质为完全背包） ，
