双栈计算算数表达式的值

一朋友去有道面试，面试官提了这样一个问题“如何从字符串形式的算术表达式中求出其值”。面试完后和几个朋友讨论后一开始认为需要采用双栈法，后来发现双栈法有缺陷，后来提出采用中缀转后缀的方法。在总结两种方法后得出了本文中的解法。

首先说一下中缀转后缀，引用http://blog.csdn.net/sgbfblog/article/details/8001651

一、后缀表达式求值

后缀表达式也叫逆波兰表达式，其求值过程可以用到栈来辅助存储。假定待求值的后缀表达式为：6  5  2  3  + 8 * + 3  +  *，则其求值过程如下：

1）遍历表达式，遇到的数字首先放入栈中，此时栈如下所示：

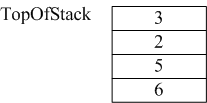
2）接着读到“+”，则弹出3和2，执行3+2，计算结果等于5，并将5压入到栈中。

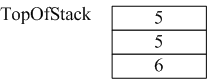
3）读到8，将其直接放入栈中。

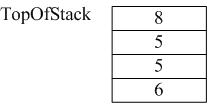
4）读到“*”，弹出8和5，执行8*5，并将结果40压入栈中。而后过程类似，读到“+”，将40和5弹出，将40+5的结果45压入栈...以此类推。最后求的值288。

 

 

二、中缀表达式转后缀表达式

2.1）规则

中缀表达式a + b*c + (d * e + f) * g，其转换成后缀表达式则为a b c * + d e * f  + g * +。

转换过程需要用到栈，具体过程如下：

1）如果遇到操作数，我们就直接将其输出。

2）如果遇到操作符，则我们将其放入到栈中，遇到左括号时我们也将其放入栈中。

3）如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。

4）如果遇到任何其他的操作符，如（“+”， “*”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到" ) "的情况下我们才弹出" ( "，其他情况我们都不会弹出" ( "。

5）如果我们读到了输入的末尾，则将栈中所有元素依次弹出。

 

2.2）实例

规则很多，还是用实例比较容易说清楚整个过程。以上面的转换为例，输入为a + b * c + (d * e + f)*g，处理过程如下：

1）首先读到a，直接输出。

2）读到“+”，将其放入到栈中。

3）读到b，直接输出。

此时栈和输出的情况如下：

 

4）读到“*”，因为栈顶元素"+"优先级比" * " 低，所以将" * "直接压入栈中。

5）读到c，直接输出。

此时栈和输出情况如下：

 

6）读到" + "，因为栈顶元素" * "的优先级比它高，所以弹出" * "并输出， 同理，栈中下一个元素" + "优先级与读到的操作符" + "一样，所以也要弹出并输出。然后再将读到的" + "压入栈中。

此时栈和输出情况如下：

 

7）下一个读到的为"("，它优先级最高，所以直接放入到栈中。

8）读到d，将其直接输出。

此时栈和输出情况如下：

 

9）读到" * "，由于只有遇到" ) "的时候左括号"("才会弹出，所以" * "直接压入栈中。

10）读到e，直接输出。

此时栈和输出情况如下：

 

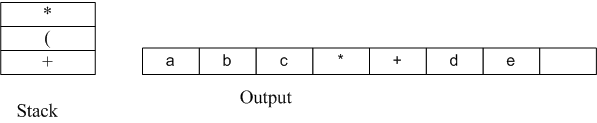
11）读到" + "，弹出" * "并输出，然后将"+"压入栈中。

12）读到f，直接输出。

此时栈和输出情况：

 

 

13）接下来读到“）”，则直接将栈中元素弹出并输出直到遇到"("为止。这里右括号前只有一个操作符"+"被弹出并输出。

 

14）读到" * "，压入栈中。读到g，直接输出。

 

15）此时输入数据已经读到末尾，栈中还有两个操作符“*”和" + "，直接弹出并输出。

至此整个转换过程完成。

 

然后介绍一下双栈法，引用http://www.cnblogs.com/mantgh/p/3973038.html

概述：
     算术表达式可能是一个数、或者是由一个左括号、一个算术表达式、一个运算符、另一个算术表达式和一个右括号组成的表达式。为了简化问题，这里定义的是未省略括号的算术表达式，它明确地说明了所有运算符的操作数，形式如下：

                                                                  （1+（（2+3）*（4*5）））

 

思路：

     表达式由括号、运算符和操作数构成，我们根据以下4中情况从左至右逐个将这些实体送入栈处理：

     1.将操作数压入操作数栈；

     2.将运算符压入运算符栈；

     3.忽略左括号；

     4.在遇到右括号时，弹出一个运算符，弹出所需数量的操作数，并将运算后的结果压入操作数栈；

    在处理完最后一个右括号时，操作数栈上只会剩下一个值，它就是表达式的计算结果。这种方法咋一看难理解，但要证明它能计算得到正确的值很简单：

    每当算法遇到一个括号包围，并由一个运算符和两个操作数组成的子式时，他都将运算符和操作数运算结果压入操作数栈。这样的结果就像是在输入中用这个值代替了该子表达式，因此用这个值代替子表达式得到的结果和原表达式相同。我们可以反复应用这个规律并得到一个最终值。

 

本文中的解法在计算结果的过程中采用双栈法，在操作符入库时采用中缀转后缀的思想，代码如下：

import java.util.Stack;

public class Solution {
    public double calculate(String expr){
        Stack<Double> num = new Stack<Double>();
        Stack<Character> operator = new Stack<Character>();
        double ret = 0;
        for (int i = 0; i < expr.length();) {
            if (expr.charAt(i)>='0' && expr.charAt(i)<='9') {
                int start = i;
                while (i < expr.length()&&expr.charAt(i)>='0' && expr.charAt(i)<='9') {
                    i++;
                }
                num.push(Double.parseDouble(expr.substring(start, i)));
                continue;
            }
            
            if (expr.charAt(i) == '+' || expr.charAt(i) == '-'|| expr.charAt(i) == '*'
                    || expr.charAt(i) == '/' || expr.charAt(i) == '(' || expr.charAt(i) == ')') {
                if (expr.charAt(i) == '(') {
                    operator.push(expr.charAt(i));
                }else if(expr.charAt(i) == ')'){
                    while (!operator.isEmpty()&&operator.peek() != '(') {
                        double second = num.pop();
                        double first = num.pop();
                        ret = operator(first, second, operator.pop());
                        num.push(ret);
                    }
                    operator.pop();
                }else {
                    while (!operator.isEmpty()&&compareOperator(expr.charAt(i), operator.peek())<=0) {
                        double second = num.pop();
                        double first = num.pop();
                        ret = operator(first, second, operator.pop());
                        num.push(ret);
                    }
                    operator.push(expr.charAt(i));
                }
            }
            i++;
        }
        
        while (operator.size() > 0) {
            double second = num.pop();
            double first = num.pop();
            ret = operator(first, second, operator.pop());
            num.push(ret);
        }
        
        return num.pop();
    }
    
    private int compareOperator(char first,char second){
        if (second == '(') {
            return 1;
        }
        int firstRank = 0;
        if (first == '+' || first == '-') {
            firstRank = 0;
        }else {
            firstRank = 1;
        }
        
        int secondRank = 0;
        
        if (second == '*' || second == '/') {
            secondRank = 1;
        }else {
            secondRank = 0;
        }
        
        return firstRank - secondRank;
    }
    
    private double operator(double first,double second,char operator){
        double ret = 0;
        switch (operator) {
        case '+':
            ret = first + second;
            break;
        case '-':
            ret = first - second;
            break;
        case '*':
            ret = first*second;
            break;
        case '/':
            ret = first/second;
            break;
        default:
            break;
        }
        return ret;
    }
}