粗劣谈谈树
本文全部摘自leetcode
树的定义
首先,先定义一个数TreeNode,定义子节点TreeNode left,TreeNode right,定义值int val;
* public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
例子树:
3 / \ 9 20 / \ 15 7
求树的深度
先从最简单的求树的深度开始入手进行递归操作
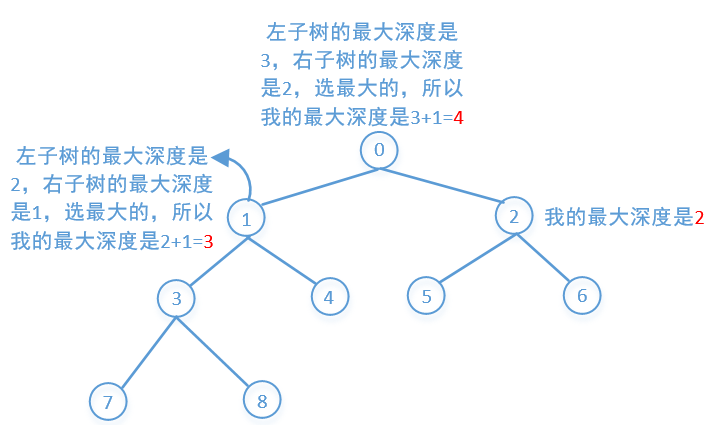
实现方案,先求root数的深度,深度为1,如果有左子节点或者右子节点,就可以使用递归,接下来,递归,递归左子树的最大深度和右子树的最大深度,并返回两者之间的最大值,加上root的深度1为树的深度,如图所示:
代码实现:
class Solution { public int maxDepth(TreeNode root) { if(root==null){return 0;} int d = Math.max(maxDepth(root.left),maxDepth(root.right))+1; return d; } }
乍一看实现起来并不难,当然还有另外的更有意思的解法:
使用队列一层一层进行遍历,也就是类似于层序遍历,遍历每一层的个数,每遍历一层,深度++,这种遍历方法还可以求出树的所有节点树。
public int maxDepth(TreeNode root) { if (root == null) return 0; //创建一个队列 Deque<TreeNode> deque = new LinkedList<>(); deque.push(root); int count = 0; while (!deque.isEmpty()) { //每一层的个数 int size = deque.size(); while (size-- > 0) { TreeNode cur = deque.pop(); if (cur.left != null) deque.addLast(cur.left); if (cur.right != null) deque.addLast(cur.right); } count++; } return count; }
树的遍历,以层序遍历为例
接下来就是我们熟悉的遍历
(1)先序遍历:FCADBEHGM:先访问根节点,再访问左子树,最后访问右子树。
(2) 后序遍历:ABDCHMGEF:先左子树,再右子树,最后根节点。
(3)中序遍历:ACBDFHEMG:先左子树,再根节点,最后右子树。
(4)层序遍历:FCEADHGBM:每一层从左到右访问每一个节点。
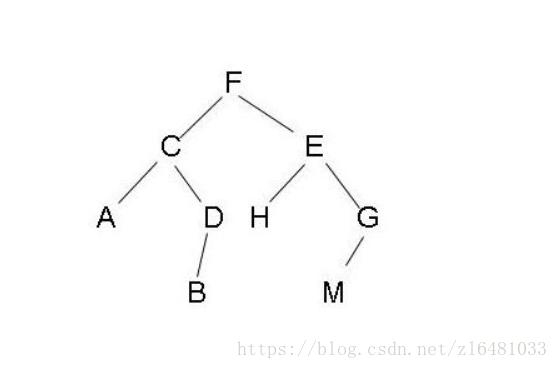
(1)先序遍历
输入:root = [1,null,2,3] 输出:[1,2,3]
使用递归进行先序遍历,注意在递归中List全文贯穿
class Solution { public List<Integer> preorderTraversal(TreeNode root) { //深度优先搜索dfs //前序遍历:先遍历root,再遍历左节点再遍历右节点 //中:左中右 //后:左右中 //使用递归,在递归中,list全递归贯穿,应该添加进参数中 List<Integer> res = new ArrayList<Integer>(); preorder(root, res); return res; } public void preorder(TreeNode root, List<Integer> res) { if (root == null) { return; } res.add(root.val); preorder(root.left, res); preorder(root.right, res); } }
(2) 中序遍历
输入:root = [1,null,2,3] 输出:[1,3,2]
跟前序遍历比,就将res.add(root.val)的位置换一下就行
public void preorder(TreeNode root, List<Integer> res) { if (root == null) { return; } preorder(root.left, res); res.add(root.val); preorder(root.right, res); }
(3) 后序遍历
同上,就将res.add(root.val)的位置换一下就行
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
public void preorder(TreeNode root, List<Integer> res) { if (root == null) { return; } preorder(root.left, res); preorder(root.right, res); res.add(root.val); }
(4) 层序遍历
以层序遍历以上例子树的结果为
[ [3], [9,20], [15,7] ]
BFS解决(广度优先搜索,对应DFS深度优先搜索)
遍历方法,使用队列进行遍历,使用队列的好处,可以保证先进先出,我上一层的内容全部出来之后,才会执行下一层的内容,也就是我必定会先遍历上一层,遍历完上一层的节点又会生成新的节点放进队列
class Solution { public List<List<Integer>> levelOrder(TreeNode root) { //边界条件判断 if (root == null) return new ArrayList<>(); //队列,使用队列的好处,可以保证先进先出,我上一层的内容全部出来之后,才会执行下一层的内容,也就是我必定会先遍历上一层,遍历完上一层的节点又会生成新的节点放进队列 Queue<TreeNode> queue = new LinkedList<>(); List<List<Integer>> res = new ArrayList<>(); //根节点入队 queue.add(root); //如果队列不为空就继续循环 while (!queue.isEmpty()) { //BFS打印,levelNum表示的是每层的结点数 int levelNum = queue.size(); //subList存储的是每层的结点值 List<Integer> subList = new ArrayList<>(); for (int i = 0; i < levelNum; i++) { //出队 TreeNode node = queue.poll(); subList.add(node.val); //左右子节点如果不为空就加入到队列中 if (node.left != null) queue.add(node.left); if (node.right != null) queue.add(node.right); } //把每层的结点值存储在res中, res.add(subList); } return res; } }
验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。有效 二叉搜索树定义如下:节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。这个问题有其他的遍历写法,不过我们使用递归,需要注意二叉树不是简单的左子树小于右子树的树,如果一开始就样子思考,就将陷入一个思想误区,无法判断以下的这种情况:
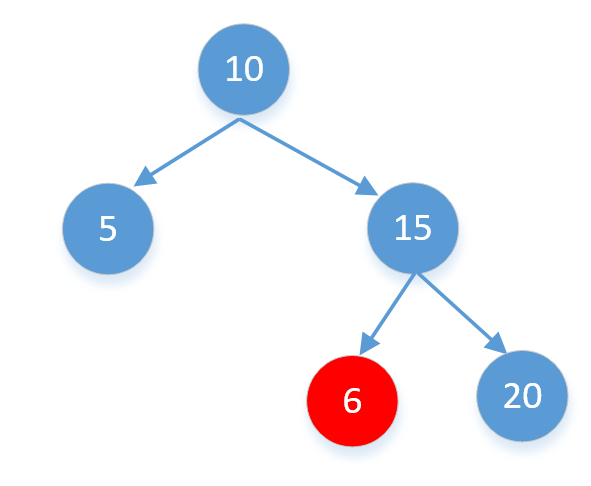
所以在实现过程中,需要注意将root节点作为一个极大极小值放进递归中进行考虑
class Solution { //验证二叉搜索树有以下必要条件 //1.左子数的所有数必须小于根节点,右子树的所有书必须大于根节点 //也就是所,在左子树中,必须出现一个最大数max为root,而在右子树中,必须出现一个最小的min为root //因此在递归中,由单参数变为了多参数,并在验证左子树的时候添加最大数max public boolean isValidBST(TreeNode root) { return isValidBST(root, null, null); } public boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) { if (root == null) { return true; } if (min != null && root.val <= min.val) { return false; } if (max != null && root.val >= max.val) { return false; } return isValidBST(root.left, min, root) && isValidBST(root.right, root, max); } }
验证对称二叉树
又称镜面二叉树,如以下二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
解决方法,递归plus,返回条件为如果左右节点都为空返回true,如果有一边为空,另一边不为空的情况,说明验证的左右节点(注意不是在一个root下的左右节点)肯定不是
对称的,进言之,如果两个的值不相等,那就一定不是对称的,依次类推,将左节点的左节点和右结点的右结点进行比较:
class Solution { public boolean isSymmetric(TreeNode root) { if(root==null){return true;} return isSymmetricHelper(root.left,root.right); } public boolean isSymmetricHelper(TreeNode left,TreeNode right){ //如果左右节点都为空,说明这个节点是叶子节点,返回true if(left==null&&right==null){return true;} //如果有一边为空,另一边不为空的情况,说明验证的左右节点(注意不是在一个root下的左右节点)肯定不是对称的, //进言之,如果两个的值不相等,那就一定不是对称的,依次类推,将左节点的左节点和右结点的右结点进行比较 if (left == null || right == null || left.val != right.val){ return false; } return isSymmetricHelper(left.left,right.right)&&isSymmetricHelper(left.right,right.left); } }
将有序数组转换为二叉搜索树
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
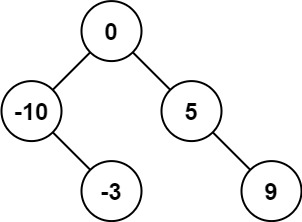
解决方案:因为是有序的数组,所以解决起来简单许多,搜索二叉树的性质为左小右大,在取root的时候应该取得中间的节点为root节点,再根据中间节点进行划分,将两边
划分为两个子树,取得子树的中间节点(start+end)>>1,也就是/2,再依次划分,左子树为对应的下标为(start,mid-1),右子树对应的下标为(mid+1,end),直到
start>end则返回空,最终得到较为平衡的二叉树:
class Solution { public TreeNode sortedArrayToBST(int[] nums) { if(nums.length==0){ return null; } return sortedTree(nums,0,nums.length-1); } public TreeNode sortedTree(int[] nums,int start,int end) { int size = nums.length; if(start>end){ return null; } //向右移动一位,/2 int mid = (end+start)>>1; //获取中间节点 TreeNode root = new TreeNode(nums[mid]); root.left = sortedTree(nums,start,mid-1); root.right = sortedTree(nums,mid+1,end); return root; } }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号