强化学习读书笔记 -- 第十三章策略梯度算法

前面介绍的强化学习算法都是根据状态价值函数或者动作价值函数来选择最优策略。 本章利用参数化方法训练一个策略模型，从而根据策略模型去选择合适的动作。记策略模型的参数为\(\theta\)，策略模型\(\pi(a|s,\theta)=\Pr\{A_t=a|S_t=s,\theta_t=\theta\}\)表示在\(t\)时刻下，给定状态\(s\)智能体选择动作\(a\)的概率。根据人为设置的评价指标\(J(\theta)\)，利用梯度法最大化\(J(\theta)\)，可得参数更新表达式为

\[\theta_{t+1}=\theta_t+\alpha\hat{\nabla J(\theta_t)} \]

这类方法被称为策略梯度法。在近似策略函数的同时近似状态价值函数，这类方法称为演员-评论家算法（actor-critic method），其中演员指的是策略模型，而评论家指的是价值函数。

1.策略模型及优点

在策略梯度法中，只要策略模型的参数是可微分的，那么策略就可以被参数化。通常策略模型是一种随机策略（与贪婪策略不同，贪婪策略是一种确定性策略），这也保证了智能体的探索能力。当动作空间是离散的且不是非常大，那么可以将状态-动作对的选择倾向进行数值化，利用参数\(\theta\)进行拟合，即\(h(s,a,\theta)\)。利用soft-max分布获得策略模型：

\[\pi(a|s,\theta)=\frac{\exp(h(s,a,\theta))}{\sum_b\exp(h(s,b,\theta))} \]

称这种策略参数化方法为动作偏好的soft-max法。这样的方式比较灵活，动作偏好参数化的方法非常多，如神经网络或线性形式，

\[h(s,a,\theta)=\theta^\Tau x(s,a), \]

其中，\(x(s,a)\)表示状态-动作对的特征向量。基于soft-max的动作偏好策略模型具有如下优点。第一，相比于随机策略\(\epsilon\)-greedy策略，它可以无限逼近确定性策略。第二，它本身还是一种随机策略。随机策略在许多实际问题当中具有更好的效果。第三，在某些问题当中，学习策略模型比学习价值函数要简单许多。例如动作空间是连续的情况，或是状态-动作空间非常庞大的情况。最后，先验知识可以植入到策略模型当中，例如将与之类似的A问题的策略模型，投入到B问题的学习中。

2.策略梯度理论

策略梯度算法具有较好的理论基础。相比于价值函数而言，策略梯度算法在学习过程中，策略模型变化更加平滑。例如在\(\epsilon\)-greedy策略中，当价值函数发生变化可能会导致贪婪动作发生变化，使得整个动作选择发生重大改变。下面介绍策略梯度理论，为了简化理论的推导过程，考虑一个不含折扣系数的回合制问题，每轮交互都从固定的初始状态\(s_0\)出发，得到准则函数：

\[J(\theta):=v_{\pi_{\theta}}(s_0) \]

其中，\(v_{\pi_\theta}\)表示在策略\(\pi_\theta\)下的状态价值函数，\(\pi_\theta\)表示在参数\(\theta\)下的策略函数。策略梯度算法的性能主要由两个方面所决定，其一是动作选择，其二是状态分布。但是在固定策略下的状态分布情况是不可知的。因此，这也是制约策略梯度算法的一个门槛。假设参数变化对于状态分布没有影响或是影响较小的情况，那么策略梯度理论是可以保证参数朝着正确的方向进行修正的。下面证明状态价值函数梯度与策略梯度有关，与状态分布梯度无关。

\[\begin{eqnarray*} \nabla v_\pi(s)&=&\nabla\left[\sum_a\pi(a|s)q_\pi(s,a)\right], \text{for all}\ s\in\mathcal{S}\\ &=& \sum_a\left[\nabla\pi(a|s)q_\pi(s,a)+ \pi(a|s)\nabla q_\pi(s,a)\right]\\ &=& \sum_a\left[\nabla\pi(a|s)q_\pi(s,a)+ \pi(a|s)\nabla \sum_{s',r}p(s',r|s,a)(r+v_\pi(s'))\right]\ 动作价值函数展开式\\ &=&\sum_a\nabla\pi(a|s)q_\pi(s,a)+\sum_a\pi(a|s)\sum_{s'}p(s'|s,a)\nabla v_\pi(s')\tag{13.1} \end{eqnarray*} \]

从上式可以看出，第二项再次出现\(\nabla v_\pi\)，而\(\sum_a\pi(a|s)p(s'|s,a)=\mu(s')\)即得到策略\(\pi\)下一次交互后的状态分布也可以记为\(\text{Pr}(s\rightarrow s',1,\pi)\)，由此可得

\[\begin{eqnarray*} \sum_a\pi(a|s)\sum_{s'}p(s'|s,a)\nabla v_\pi(s')=\sum_{s'}\text{Pr}(s\rightarrow s',1,\pi)\nabla v_\pi(s') \end{eqnarray*} \]

对式（13.1）进一步展开可得

\[\begin{eqnarray*} \nabla v_\pi(s) &=& \sum_a\nabla\pi(a|s)q_\pi(s,a)\\ &&+ \sum_a\pi(a|s)\sum_{s'}p(s'|s,a)\sum_{a'}\nabla\pi(a'|s')q_\pi(s',a')\\ &&+ \sum_a\pi(a|s)\sum_{s'}p(s'|s,a)\sum_{a'}\pi(a'|s')\sum_{s''}p(s''|s',a')\sum_{a''}\nabla\pi(a''|s'')q_\pi(s'',a'')\\ && +\cdots\cdots\\ &=&\text{Pr}(s\rightarrow s,0,\pi)\sum_a\nabla\pi(a|s)q_\pi(s,a)\\ &&+\sum_{s'}\text{Pr}(s\rightarrow s',1,\pi)\sum_{a'}\nabla\pi(a'|s')q_\pi(s',a')\\ &&+\sum_{s''}\text{Pr}(s\rightarrow s'',2,\pi)\sum_{a''}\nabla\pi(a''|s'')q_\pi(s'',a'')\\ &&+\cdots\cdots\\ &&+\sum_{s^{(n)}}\text{Pr}(s\rightarrow s'',n,\pi)\sum_{a''}\nabla\pi(a''|s'')q_\pi(s'',a'')\\ &=&\sum_{x\in\mathcal{S}}\sum_{k=0}^\infin\text{Pr}(s\rightarrow x,k,\pi)\sum_a\nabla\pi(a|x)q_\pi(x,a). \end{eqnarray*} \]

令\(\sum_{k=0}^\infin\text{Pr}(s_0\rightarrow s,k,\pi)=\eta(s)\)，考虑\(\nabla J(\theta)\)，

\[\begin{eqnarray*} \nabla J(\theta) &=& \nabla v_\pi(s_0)\\ &=&\sum_s\eta(s)\sum_a\nabla\pi(a|s)q_\pi(s,a)\\ &=&\sum_{x}\eta(x)\sum_s\frac{\eta(s)}{\sum_x\eta(x)}\sum_a\nabla\pi(a|s)q_\pi(s,a)\\ &=&\sum_x\eta(x)\sum_s\mu(s)\sum_a\nabla\pi(a|s)q_\pi(s,a) \\ &=&\text{constant}*\sum_s\mu(s)\sum_a\nabla\pi(a|s)q_\pi(s,a) \\ &\propto&\sum_s\mu(s)\sum_a\nabla\pi(a|s)q_\pi(s,a),\tag{13.2} \end{eqnarray*} \]

其中，\(\mu(s)\)表示策略\(\pi\)下的状态分布；对于回合制交互，constant等价于回合制交互的平均轨迹长度，对于无终止状态的交互，constant等于1。从上式可以看出，\(\nabla J(\theta)\)与策略梯度有关，与状态分布梯度无关。证明完毕。

3.REINFORCE算法：蒙特卡洛策略梯度算法

考虑式（13.2），常数项可以由学习率\(\alpha\)所吸收，因此，该式可以看作是基于策略\(\pi\)下的状态分布的期望，即

\[\nabla J(\theta)=E_{\pi^s}\left[\sum_aq_\pi(s,a)\nabla \pi(a|s)\right]\tag{13.3} \]

采用随机采样的方式可得，参数\(\theta_t\)的随机梯度更新式为

\[\theta_{t+1}=\theta_t+\alpha\sum_a\hat{q}_\pi(S_t,a,w)\nabla \pi(a|S_t,\theta_t), \]

其中，\(\hat{q}\)表示当前时刻下动作价值的估计。但这并不是REINFORCE算法，因为式（13.3）需要考虑所有的动作。进一步变换可得

\[\begin{eqnarray*} \sum_aq_\pi(s,a)\nabla \pi(a|s)&=&\sum_a\pi(a|S_t,\theta)q_\pi(S_t,a)\frac{\nabla\pi(a|S_t,\theta)}{\pi(a|S_t,\theta)}\\ &=&E_{\pi^a}\left[q_\pi(S_t,A_t)\frac{\nabla\pi(A_t|S_t,\theta)}{\pi(A_t|S_t,\theta)}\right]\\ &=&E_{\pi^a}\left[G_t\frac{\nabla\pi(A_t|S_t,\theta)}{\pi(A_t|S_t,\theta)}\right], as\ E_\pi[G_t|S_t,A_t]=q_\pi(S_t,A_t) \end{eqnarray*} \]

上式可以看作是基于策略\(\pi\)下的动作选择的期望。对状态和动作的随机采样可得更新式为

\[\begin{eqnarray*} \theta_{t+1}&=&\theta_t+\alpha G_t\frac{\nabla\pi(A_t|S_t,\theta_t)}{\pi(A_t|S_t,\theta_t)}\\ &=&\theta_t+\alpha G_t\nabla\ln\pi(A_t|S_t,\theta_t) \end{eqnarray*} \]

其中，\(G_t\)表示回报。这就是REINFORCE算法的核心式。简单分析一下，更新增量与回报成正比，与选择动作的概率成反比。这样的可以看出，智能体的学习倾向于回报较高的动作，对于意料中的状态-动作对的学习力度会下降。下面给出蒙特卡洛策略梯度算法的伪代码实现，这里引入折扣系数，如下图所示。

值得注意的是，基于蒙特卡洛的REINFORCE算法具有很高的方差，需要设置很小的学习率，因此收敛速度较慢。

考虑第一节中的动作偏好的soft-max法，计算\(\nabla\ln\pi(a|s,\theta)\)。已知

\[\begin{eqnarray*} \pi(a|s,\theta)&=&\frac{\exp(h(s,a,\theta))}{\sum_b\exp(h(s,b,\theta))}\\ &=&\frac{\exp(\theta^\Tau x(s,a))}{\sum_b\exp(\theta^\Tau x(s,b))}\\ &=&\frac{h_a}{\sum_bh_b} \end{eqnarray*} \]

可得\(\nabla\pi(a|s,\theta)\)为

\[\begin{eqnarray*} \nabla\pi(a|s,\theta)&=&\frac{h_ax(s,a)\sum_bh_b-h_a\sum_bh_bx(s,b)}{(\sum_bh_b)^2} \end{eqnarray*} \]

最终可得

\[\begin{eqnarray*} \nabla\ln\pi(a|s,\theta)&=&\frac{\nabla\pi(a|s,\theta)}{\pi(a|s,\theta)}\\ &=&\frac{x(s,a)\sum_bh_b-\sum_bh_bx(s,b)}{\sum_bh_b}\\ &=&x(s,a)-\sum_b\frac{h_b}{\sum_bh_b}x(s,b)\\ &=&x(s,a)-\sum_b\pi(b|s,\theta)x(s,b) \end{eqnarray*} \]

计算完毕。

4.基于基准的REINFORCE算法

根据策略梯度理论（13.2）给出基于基准的策略梯度：

\[\nabla J(\theta)\propto\sum_s\mu(s)\sum_a(q_\pi(s,a)-b(s))\nabla\pi(a|s,\theta). \]

值得注意的是，基准\(b(s)\)只要与动作\(a\)无关，则不会对策略梯度产生影响：

\[\sum_ab(s)\nabla\pi(a|s,\theta)=b(s)\nabla\sum_a\pi(a|s,\theta)=b(s)\nabla 1=0 \]

由此可得，更具一般性的基于基准的REINFORCE算法的更新式：

\[\theta_{t+1}=\theta_t+\alpha(G_t-b(S_t))\frac{\nabla\pi(A_t|S_t,\theta_t)}{\pi(A_t|S_t,\theta_t)}. \]

从期望的角度来讲，添加基准并不会影响最终结果的期望，但是却能有效的降低学习过程中的方差。\(b(s)\)的选择既可以为一个常数值，也可以通过学习状态价值函数\(\hat{v}(S_t,w)\)。下面给出基于基准的REINFORCE算法的伪代码实现，如下图所示。

在伪代码中需要分别设置状态价值函数和策略函数的学习率\(\alpha^w\)和\(\alpha^\theta\)，通常\(\alpha^w>\alpha^\theta\)。学习率\(\alpha^w\)的设置可以参考第九章第六节中的经验公式，\(\alpha^w=0.1/E[\|\nabla\hat{v}(S_t,w)\|_\mu^2 ]\)。目前没有合适的方式选择\(\alpha^\theta\)，只能采用试错法。

5.演员-评论家算法（Actor-Critic methods）

演员-评论家算法（简称AC算法）本质上与基于基准的REINFORCE算法是一致的。AC算法是一种在线算法，引入了TD算法的更新机制，用每一时刻的估计值替换状态价值或动作价值的采样值。由此可得，单步AC算法的参数更新式为

\[\begin{eqnarray*} \theta_{t+1}&=&\theta_t+\alpha(G_{t:t+1}-\hat{v}(S_t,w))\frac{\nabla\pi(A_t|S_t,\theta_t)}{\pi(A_t|S_t,\theta_t)}\\ &=&\theta_t+\alpha(R_{t+1}+\gamma\hat{v}(S_{t+1},w)-\hat{v}(S_t,w))\frac{\nabla\pi(A_t|S_t,\theta_t)}{\pi(A_t|S_t,\theta_t)}\\ &=&\theta_t+\alpha\delta_t\frac{\nabla\pi(A_t|S_t,\theta_t)}{\pi(A_t|S_t,\theta_t)} \end{eqnarray*} \]

下面给出AC算法的伪代码实现，如下图所示。

当然，可以将单步AC算法扩展至多步AC算法。需要注意的是，此时\(\theta\)的更新式需要乘上\(\gamma^n\)。另外，也可以将第12章的有效循迹引入到AC算法中。下面给出基于有效循迹的AC算法的伪代码，如下图所示。

6.连续问题下的策略梯度

前面考虑的都是回合制问题下的策略梯度算法，在连续问题中，需要引入平均奖励的设定帮助解决强化学习问题，具体细节可以回顾第十章第3节的内容。简单回顾，平均奖励定义为

\[\begin{eqnarray} J(\theta)=r(\pi)&:=&\lim_{h\rightarrow\infin}\frac{1}{h}\sum_{t=1}^h\mathbb{E}[R_t|A_{0:t-1}\sim\pi]\\ &=&\lim_{t\rightarrow\infin}\mathbb{E}[R_t|A_{0:t-1}\sim\pi]\\ &=&\sum_s\mu_\pi(s)\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)r \end{eqnarray} \]

其中，\(\mu_\pi(s)\)为策略\(\pi\)下稳定的状态分布，即\(\mu_\pi(s)=\lim_{t\rightarrow\infin}\Pr\{S_t=s|A_{0:t-1}\sim\pi\}\)。通过状态转移可得下一状态同样满足稳定的状态分布：

\[\sum_s\mu_\pi(s)\sum_a\pi(a|s)p(s'|s,a)=\mu_\pi(s')。 \]

面给出连续情况下基于有效循迹的AC算法的伪代码，如下图所示。

下面证明，连续问题下的策略梯度理论，即策略梯度仅与价值函数梯度有关，与状态分布梯度无关。在此之前，回顾一下，连续问题下的回报为

\[G_t:=R_{t+1}-r(\pi)+R_{t+2}-r(\pi)+R_{t+3}-r(\pi)+\cdots. \]

其中，\(r(\pi)\)是平均奖励，同时也是评价指标\(J(\theta)\)。

参考式（13.1）可得

\[\begin{eqnarray*} \nabla\hat{v}_\pi(s)&=&\sum_a\left[\nabla\pi(a|s)q_\pi(s,a)+\pi(a|s)\nabla\sum_{s',r}p(s',r|s,a)(r-r(\theta)+v_\pi(s'))\right]\\ &=&\sum_a\left[\nabla\pi(a|s)q_\pi(s,a)+\pi(a|s)\sum_{s',r}p(s',r|s,a)(-\nabla r(\theta)+\nabla v_\pi(s'))\right]\\ &=&\sum_a\left[\nabla\pi(a|s)q_\pi(s,a)-\pi(a|s)\nabla r(\theta)+\pi(a|s)\sum_{s'}p(s'|s,a)\nabla v_\pi(s')\right], \end{eqnarray*} \]

对上式进行整理可得，

\[\nabla r(\theta)=\sum_a\left[\nabla\pi(a|s)q_\pi(s,a)+\pi(a|s)\sum_{s'}p(s'|s,a)\nabla v_\pi(s')\right]-\nabla\hat{v}_\pi(s) \]

下面需要借助一个事实，\(r(\theta)\)与状态\(s\)无关，因此可以在上式左右两侧添加状态分布的加权平均，即\(\sum_s\mu(s)=1\)。可得

\[\begin{eqnarray*} \nabla r(\theta)&=&\sum_s\mu(s)\sum_a\nabla\pi(a|s)q_\pi(s,a)+\sum_s\mu(s)\sum_a\pi(a|s)\sum_{s'}p(s'|s,a)\nabla \hat{v}_\pi(s')-\sum_s\mu(s)\nabla\hat{v}_\pi(s)\\ &=&\sum_s\mu(s)\sum_a\nabla\pi(a|s)q_\pi(s,a)+\sum_{s'}\mu(s')\nabla\hat{v}_\pi(s')-\sum_s\mu(s)\nabla\hat{v}_\pi(s)\\ &=&\sum_s\mu(s)\sum_a\nabla\pi(a|s)q_\pi(s,a). \end{eqnarray*} \]

从上式可看出，连续问题下的策略梯度仅与价值函数梯度有关，与状态分布梯度无关。

7.连续动作空间下的策略模型

策略梯度算法不仅可以应用在离散动作空间下的强化学习问题中，也可以应用在连续动作空间的问题。连续动作空间意味着可选动作具有无数个，通常采用正太分布来拟合可选动作的分布情况。定义策略模型为

\[\pi(a|s,\theta)=\frac{1}{\sigma(s,\theta)\sqrt{2\pi}}\exp(-\frac{(a-\mu(s,\theta))^2}{2\sigma(s,\theta)^2}), \]

其中，参数\(\theta=[\theta_\mu;\theta_\sigma]\)，\(\mu\)和\(\sigma\)是关于状态\(s\)和\(\theta\)的映射函数。该函数可以采用最为简单的线性函数，如

\[\begin{eqnarray*} \mu(s,\theta)=\theta_\mu^\Tau x_\mu(s),\quad \sigma(s,\theta)=\exp(\theta_\sigma^\Tau x_\sigma(s)). \end{eqnarray*} \]

其中，\(x_\mu(s)\)和\(x_\sigma(s)\)表示状态\(s\)的特征向量。对于方差函数\(\sigma(\cdot)\)之所以采用指数的形式，可以便于计算策略模型关于\(\theta_\sigma\)的偏导，同时也能保证\(\sigma\)取正数。

下面证明

\[\nabla\ln\pi(a|s,\theta_\mu)=\frac{1}{\sigma(s,\theta)}(a-\mu(s,\theta))x_\mu(s),\\ \nabla\ln\pi(a|s,\theta_\sigma)=\left[\frac{(a-\mu(s,\theta))^2}{\sigma(s,\theta)^2}-1\right]x_\sigma(s). \]

首先计算

\[\begin{eqnarray*} \nabla_{\theta_\mu}\pi(a|s,\theta) &=& \pi(a|s,\theta)(-\frac{2(a-\mu(s,\theta))(-\nabla_{\theta_\mu}\mu(s,\theta))}{2\sigma(s,\theta)^2})\\ &=&\pi(a|s,\theta)\frac{(a-\mu(s,\theta))x_\mu(s)}{\sigma(s,\theta)^2}\\ \nabla_{\theta_\sigma}\pi(a|s,\theta)&=&\pi(a|s,\theta)(-\sigma(s,\theta)^{-1}\nabla_{\theta_\sigma}\sigma(s,\theta))+\pi(a|s,\theta)((a-\mu(s,\theta))^2\sigma(s,\theta)^{-3}\nabla_{\theta_\sigma}\sigma(s,\theta)\\ &=&-\pi(a|s,\theta)x_\sigma(s)+\pi(a|s,\theta)(a-\mu(s,\theta))^2\sigma(s,\theta)^{-2}x_\sigma(s)\\ &=&\pi(a|s,\theta)\left[\frac{(a-\mu(s,\theta))^2}{\sigma(s,\theta)^2}-1\right]x_\sigma(s) \end{eqnarray*} \]

根据

\[\nabla\ln\pi(a|s,\theta)=\frac{\nabla\pi(a|s,\theta)}{\pi(a|s,\theta)} \]

可以得到最终结果。证明完毕。

8.总结

本章主要学习了策略梯度理论，将策略进行参数化而不像之前的章节中通过对比\(Q\)函数去选择合适的动作，这样一类算法称之为策略梯度算法。学习策略模型具有很多优点：策略模型可以拟合动作选择的概率模型；策略模型是一种随机策略，可以有效平衡探索和挖掘之间的矛盾，随着训练次数的不断增加，策略模型将逐步逼近确定性策略；策略模型适用于连续的动作空间，这是常用的\(\epsilon\)-greedy随机策略很难做到的，并且相比之下，策略模型具有更好适应性。

本章主要介绍了REINFORCE算法和基于基准的REINFORCE算法，这两个算法是基于蒙特卡洛机制下实现的。还介绍了更为常用且性能更好的，“演员-评论家”算法，该算法采用TD和自举机制，具有更快的学习速度，且方差较小。

9.实验

实验1：走廊问题

考虑下图中的小走廊网格世界。在没到达终止状态前，每一步动作的奖励是\(R=−1\)，到达终止状态时，奖励\(R=0\)。在这三种非终结状态中，每种状态都只有两个动作向左和向右。这些动作在第一种和第三种状态下正常变化（如在第一种状态下，向左不会引起移动），但在第二种状态下，动作导致的状态转换是相反的（如向左会向右移动）。这个问题的困难在于，在函数近似的情况下，所有的状态的特征都是一样的。定义所有状态-动作对的特征为\(x(s,\text{right})=[1，0]^\Tau\)和\(x(s,\text{left})=[0，1]^\Tau\)。当采用\(\epsilon\)-greedy策略时，贪婪动作的概率为\(1-\epsilon/2\)，另一个动作的概率为\(\epsilon/2\)。那么智能体需要学习到一个特定的概率使得回报的期望最大。但是，如果采用确定性策略，则无法学习到解决方案。

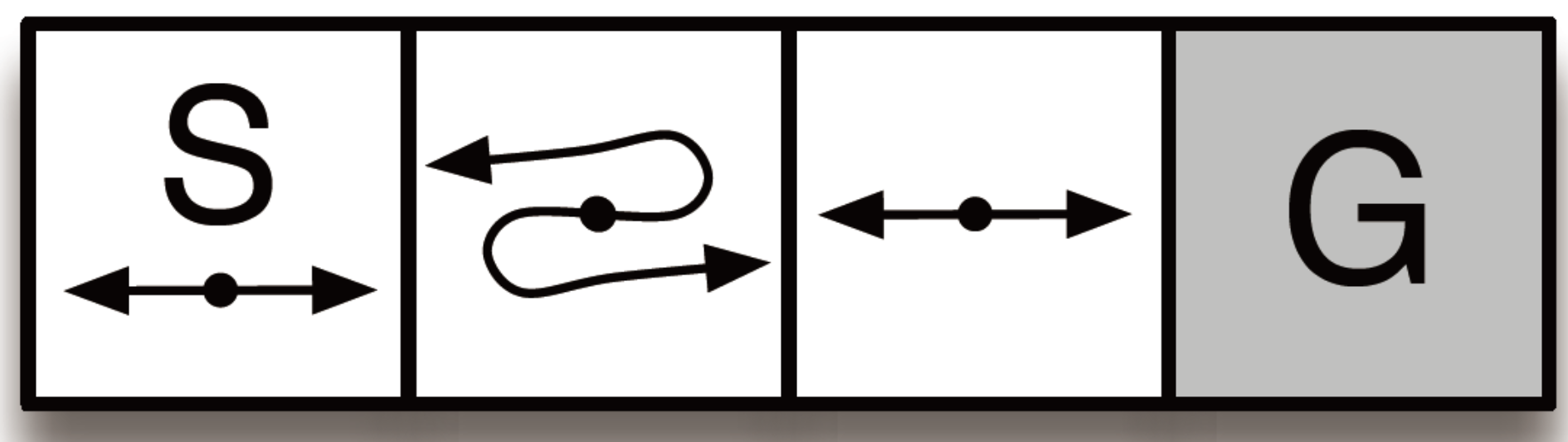
首先，计算一下最大化初值状态价值\(v_1\)的最优概率，定义选择向右动作的概率为\(p\)，利用状态价值的递推式\(v(S_t)=E[R_{t+1}+\gamma v(S_{t+1})]\)可得

\[\begin{eqnarray*} v_1&=&p(-1+v_2)+(1-p)(-1+v_1)\\ v_2&=&p(-1+v_1)+(1-p)(-1+v_3)\\ v_3&=&p(-1+v_T)+(1-p)(-1+v_2) \end{eqnarray*} \]

经过整理可得

\[\begin{eqnarray*} v_1&=&v_2-1/p\\ v_2&=&pv_1+(1-p)v_3-1\\ v_3&=&(1-p)v_2-1 \end{eqnarray*} \]

最后可得

\[v_1=\frac{(2p-4)}{p(1-p)}. \]

由此，可以分析一下状态价值\(v_1\)随\(p\)变化的曲线，如下图所示。

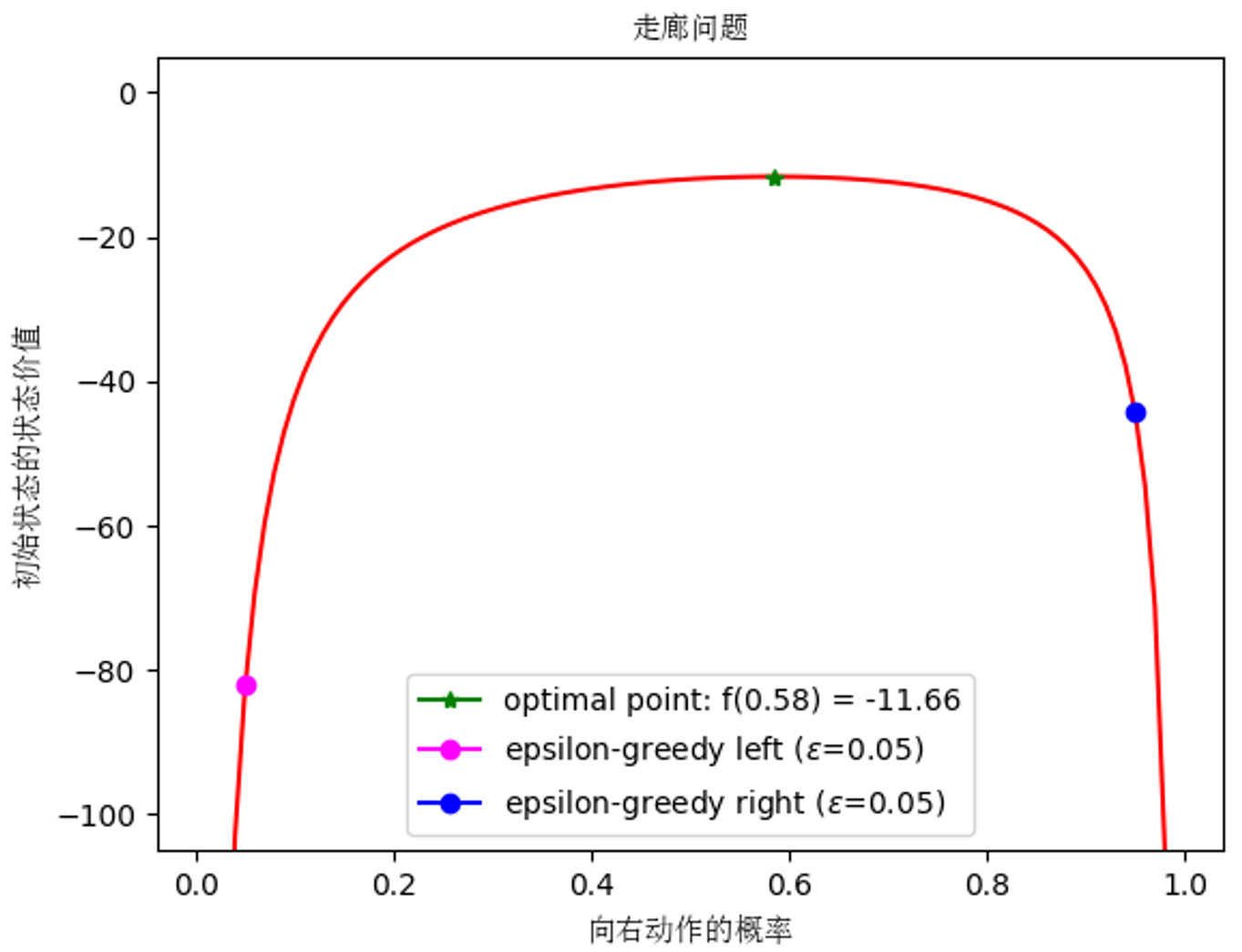
从实验结果可以看出，当向右的概率为\(p=0.58\)时，期望回报最大\(E(G)=-11.66\)，即\(\epsilon=0.84\)。这个问题是反直觉的，随机行为比确定性行为的收益要高很多。从另一种角度来看，学习行为的概率分布有时比选择最佳动作更好。当采用\(\epsilon\)-greedy策略，当\(\epsilon=0.05\)时，向右的贪婪动作明显好于向左的贪婪动作。

下面利用REINFORCE算法去解决走廊问题，其核心更新公式为

\[\theta_{t+1}=\theta_t+\alpha\gamma^tG_t\nabla\ln\pi(A_t|S_t,\theta), \]

其中，策略\(\pi\)采用动作偏好的soft-max法，即\(h(s,a,\theta)=\theta^\Tau x(s,a)\)，可得策略\(\pi\)为

\[\pi(a|s,\theta)=\frac{\exp(h(s,a,\theta))}{\sum_b\exp(h(s,b,\theta))}. \]

程序实现过程中，采用面向对象编程模式将环境、智能体和实验方法分别进行定义，即ShortCorridor类、ReinforceAgent类和trival()方法，具体代码参照随书代码第13章short_corridor.py。其中核心代码如下所示。主要展示了回报\(G_t\)的计算和参数\(\theta_t\)的更新过程。

# learn theta
G = np.zeros(len(self.rewards))
G[-1] = self.rewards[-1]

# v_t = R_{t+1}+\gamma*v_{t+1}
for i in range(2, len(G) + 1):
    G[-i] = self.gamma * G[-i + 1] + self.rewards[-i]

gamma_pow = 1

for i in range(len(G)):
    j = 1 if self.actions[i] else 0
    pmf = self.get_pi()
    # 策略梯度的计算
    grad_ln_pi = self.x[:, j] - np.dot(self.x, pmf)
    update = self.alpha * gamma_pow * G[i] * grad_ln_pi

    self.theta += update
    gamma_pow *= self.gamma

在实验过程中，初始参数为\(\theta_0=[-1.47,1.47]\)，学习率\(\alpha\)分别取\(2*10^{-3},2*10^{-4},2*10^{-5}\)，\(\gamma=1\)。最优回报期望按照上面所讨论的是\(E(G)=-11.66\)，用一条红色虚线表示。为了保证实验结果的一致性，共进行100轮重复实验，每轮实验共进行1000轮游戏。实验结果如下图所示。

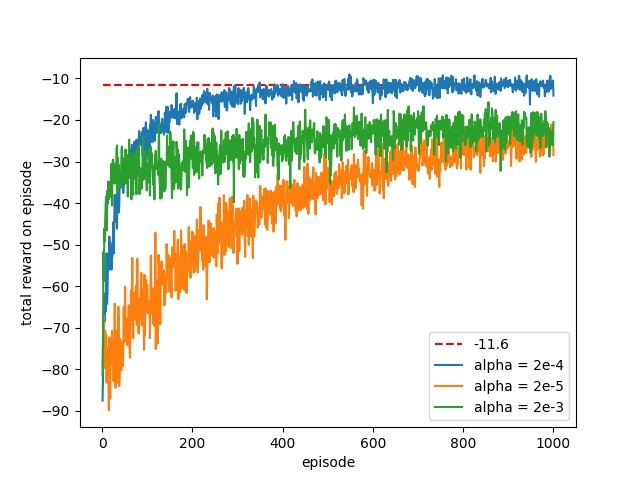
从实验结果可以看出，学习率过大使得回报采样的方差较大，智能体的学习效果就会变得不理想。采用较小的学习率，效果不理想，学习速率太慢，实验结果如下图所示（与书上的实验结果图相差很远）。

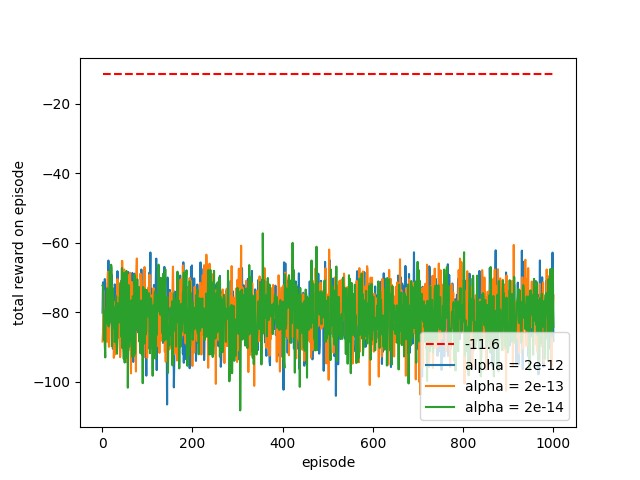
需要指出的是，初始参数的设置对结果的影响也比较大，其原因在于当初始参数设置不好导致策略变成确定性策略，使得每轮交互轨迹过长，智能体学习的效率会严重下降。在代码中，会进行一个限制操作，\(\epsilon\)最小不能小于0.05，即\(\min\pi(a)\geq0.05\)，这样使得智能体始终采用随机策略探索。当然也可以限制智能体每局的交互次数的上限，这样也能防止智能体困在交互中无法终结。

下面利用基于基准的REINFORCE算法解决走廊问题，其核心更新公式为

\[\begin{eqnarray*} w_{t+1}&=&w_t+\alpha^w\delta_t\nabla\hat{v}(S_t,w)\\ \theta_{t+1}&=&\theta_t+\alpha^\theta\gamma^t\delta_t\nabla\ln\pi(A_t|S_t,\theta)\\ \delta_t&=&G_t-\hat{v}(S_t,w) \end{eqnarray*} \]

在本实验中，因为无法区分智能体所处的状态，因此所有状态可以采用同一个状态价值估计\(\hat{v} = w\)，可得\(\nabla\hat{v}=1\)。其核心代码如下所示。

# learn theta
gamma_pow = 1

for i in range(len(G)):
    # w是状态价值的估计值
    self.w += self.alpha_w * (G[i] - self.w)
    j = 1 if self.actions[i] else 0
    pmf = self.get_pi()
    grad_ln_pi = self.x[:, j] - np.dot(self.x, pmf)
    update = self.alpha * gamma_pow * (G[i] - self.w) * grad_ln_pi

    self.theta += update
    gamma_pow *= self.gamma

实验过程中对比基于基准和没有基准的REINFORCE算法，实验结果如下图所示。

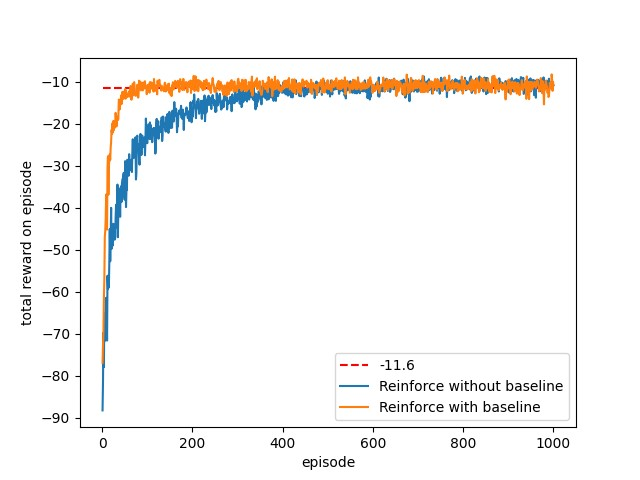
从实验结果可以看出，基于基准的REINFORCE算法的学习速度非常快，这个就是actor-critic算法架构的强大威力。需要指出的是，状态价值函数和策略函数的学习率\(\alpha^w\)和\(\alpha^\theta\)通常差1~2个数量级，\(\alpha^w>10\alpha^\theta\)。