强化学习读书笔记 -- 第十二章有效循迹

有效循迹是强化学习中的一个重要机制。几乎所有的时序差分（TD）学习方法都可以与之结合来提升学习效率，例如Sarsa算法、Q-learning算法。有效循迹方法将蒙特卡洛（MC）方法与TD方法相结合，使得MC方法同样可以采用逐步更新的方式，传统的蒙特卡洛MC方法需要到终止状态才进行更新。有效循迹方法具有较好的计算优势（因为采取递推的形式），它将短期记忆向量--有效循迹\(z_t\in\R^d\)与长期记忆向量--参数向量\(w_t\in\R^d\)相结合，例如与传统\(n\)步方法相比，有效循迹的主要计算优势在于只需要存储单个循迹向量，而不需要存储\(n\)个状态特征向量。

上面介绍了有效循迹方法的优点。这里介绍有效循迹的思想。本书前面介绍的大部分算法都是前向视角，通过估计未来一步或者多步的状态价值来更新当前的价值。但是有效循迹方法是一种后向视角算法，将数据回溯进行更新，并与前向TD算法相结合，可以得到更加强大的强化学习算法。

1.\(\lambda\)-回报

回顾\(n\)步回报的定义为

\[G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1}R_{t+n}+\gamma^n\hat{v}(S_{t+n},w_{t+n-1}),\ 0\leq t\leq T-n \]

其中，\(\hat{v}(s,w)\)表示基于参数\(w\)的状态\(s\)的估计价值。\(T\)表示终止状态的时刻。

\(\lambda\)-回报是不同步数回报的加权平均，例如\(\frac{1}{2}G_{t:t+2}+\frac{1}{2}G_{t:t+4}\)。为了保证回报统计性质不变，即\(\mathbb{E}[G_t]=v(s_t)\)，权重之和应该为1。直接将\(\lambda\)-回报替换目标状态价值，直接应用于本书前面所提到的强化学习方法中，通常称为复合更新（compound update）。当与TD算法相结合也称为\(TD(\lambda)\)算法，该算法也是前向视角。定义理想情况下的\(\lambda\)-回报为

\[\begin{eqnarray} G_t^\lambda &=& (1-\lambda)\sum_{n=1}^\infin \lambda^{n-1}G_{t:t+n}\tag{12.1}\\ &=& (1-\lambda)\sum_{n=1}^\infin \lambda^{n-1}(R_{t+1}+\gamma G_{t+1:t+n})\\ &=& R_{t+1}+\gamma(1-\lambda)\sum_{n=1}^\infin\lambda^{n-1}G_{t+1:t+n}\\ &=& R_{t+1}+\gamma(1-\lambda)(\hat{v}(S_{t+1},w)+\lambda\sum_{n=1}^\infin\lambda^{n-1}G_{t+1:t+n+1})\ (注意G_{t+1:t+1}=\hat{v}(S_{t+1},w))\\ &=& R_{t+1}+\gamma\lambda G_{t+1}^\lambda+\gamma(1-\lambda)\hat{v}(S_{t+1},w) \end{eqnarray} \]

分析一下式（12.1），复合更新只有当最长累积回报计算得到后才能进行。\(\lambda\)-回报中的权重随着步数增加而逐渐减小，其系数变化曲线如下图所示。（这里个人觉得应该倒过来更合适，因为步长越长得到的估计结果越接近蒙特卡洛采样，具有无偏性。但是不适用与无穷轨迹长度的情况，可以尝试改进。）

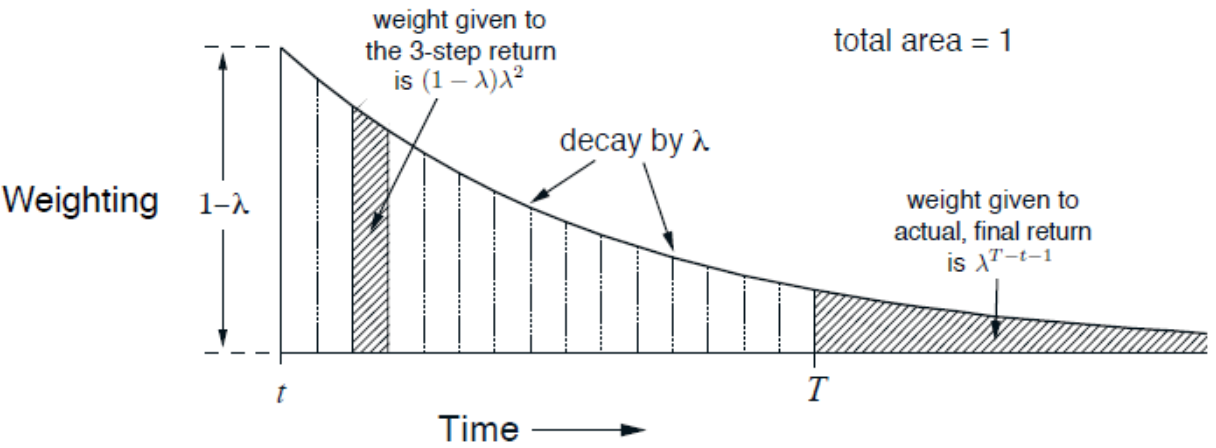
在实际应用中，为了避免更新延迟过大应该设定最大步长。定义含终止状态的\(\lambda\)-回报为

\[\begin{equation*} G_t^\lambda=(1-\lambda)\sum_{n=1}^{T-t-1}\lambda^{n-1}G_{t:t+n}+\lambda^{T-t-1}G_t \end{equation*} \]

当\(\lambda=0\)，\(G_t^\lambda=G_{t:t+1}\)即单步回报，等价于Sarsa算法。当\(\lambda=1\)，\(G_t^\lambda=G_t\)即采样回报，等价于MC算法。

2.离线\(\lambda\)-回报算法

将\(\lambda\)-回报直接应用于强化学习，称为离线\(\lambda\)-回报算法（offline \(\lambda\)-returen algorithm）。之所以是离线，因为该算法采用的是蒙特卡洛方法，即必须完成一轮交互后才能计算更新。使用半梯度方式更新参数：

\[w_{k+1}=w_k+\alpha[G_k^\lambda-\hat{v}(S_k,w_k)]\nabla\hat{v}(S_k,w_k),\ k=0,1,\ldots,T-1 \]

当\(0<\lambda<1\)，离线\(\lambda\)-回报算法相当于介于Sarsa算法和MC算法之间，在实际应用中其效果与TD(n)算法效果相当。离线\(\lambda\)-回报算法也是前向算法的一种，即当达到一个状态后，就不再需要使用之前的状态了。更形象的表现如下图所示。

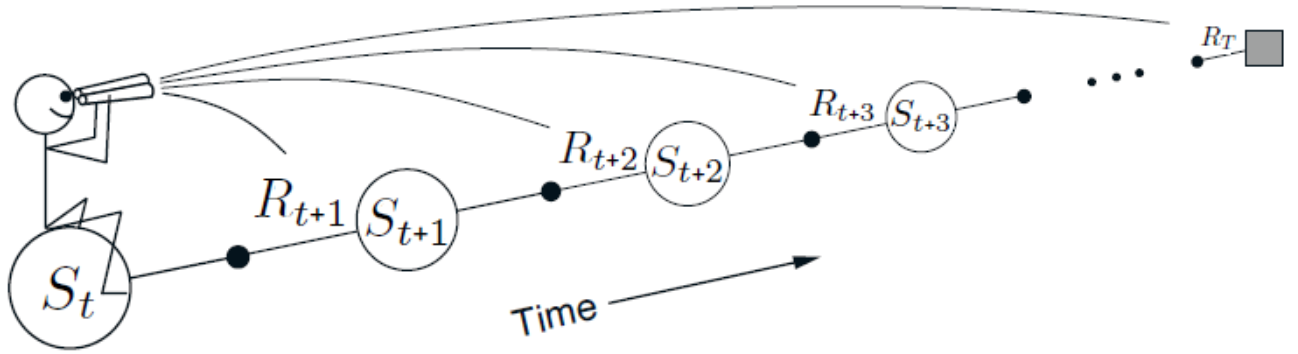
值得注意的是，离线回报算法并未引入有效循迹方法，同时它是一种前向算法。具体算法的实现和效果可以查看实验1。

3. TD(\(\lambda\))算法

TD(\(\lambda\))算法是第一个融入后向视角的强化学习算法。它在离线\(\lambda\)-回报算法的基础上做了三点改进。一是在每一步交互中都更新权重向量\(w\)；二是它的计算量均匀分配在交互的过程中，而非集中在一轮交互结束后进行；三是它可以应用在连续问题上。

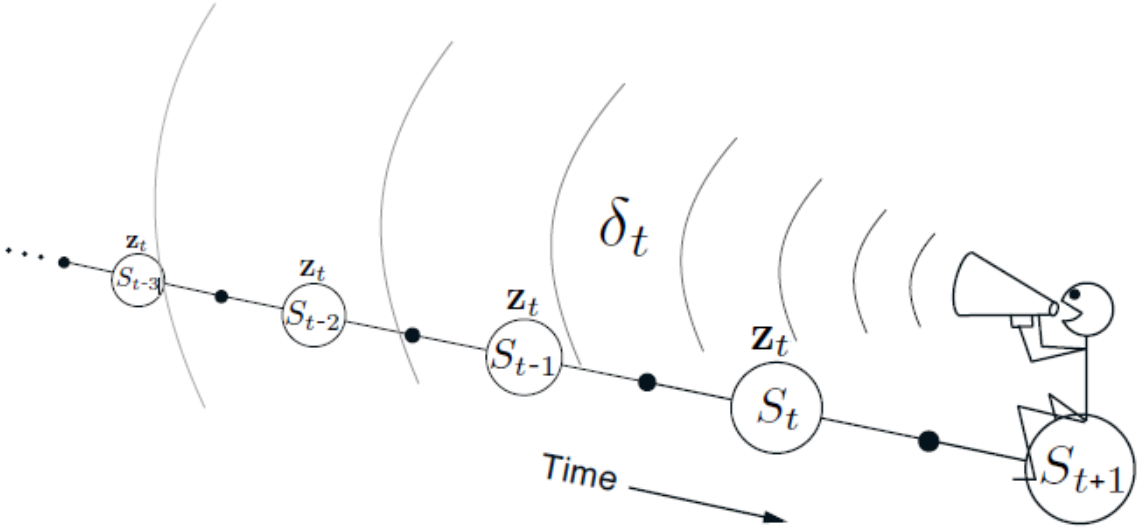
在TD(\(\lambda\))算法中，需要引入有效循迹\(z_t\)，\(z_t\)初始为0，由累加项和衰减项所构成：

\[z_t=\gamma\lambda z_{t-1}+\nabla\hat{v}(S_t,w_t),\ z_{-1}=0,\ 0\leq t\leq T. \]

有效循迹\(z_t\)的更新与动量方式是有所区别的，更像是一种梯度方向的平滑处理。\(z_t\)是一种短期记忆，旧信息随着时间的增加而逐步衰减，同时它是一种后向视角，保存了之前遇到的状态信息，如下图所示。正如本章开头所述，在函数拟合的情况下，权重向量是一个长期记忆向量，而有效循迹向量是一个短期记忆向量。

对单步TD(\(\lambda\))算法来说，TD误差为

\[\delta_t=R_{t+1}+\gamma\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t) \]

其参数更新公式为

\[w_{t+1}=w_t+\alpha\delta_tz_t. \]

综上可得总结得到TD(\(\lambda\))算法的伪代码如下图所示。具体实现和算法效果可以参照实验1。

TD(\(\lambda\))是一种典型的后向算法。当\(\lambda=1\)，循迹衰减系数只有\(\gamma\)。当\(\lambda=0\)，TD(0)算法就是Sarsa算法。

线性TD(\(\lambda\))的收敛关系为

\[\overline{VE}(w_\infin)\leq\frac{1-\gamma\lambda}{1-\gamma}\min_w\overline{VE}(w) \]

证明如下，

\[\begin{eqnarray*} G_t^\lambda-\hat{v}(S_t,w_t) &=& R_{t+1}+\gamma\lambda G_{t+1}^\lambda+\gamma(1-\lambda)\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t)\\ &=&(R_{t+1}+\gamma\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t))+\gamma\lambda(G_{t+1}^\lambda-\hat{v}(S_{t+1},w_t))\\ &=&\delta_t+\gamma\lambda(G_{t+1}^\lambda-\hat{v}(S_{t+1},w_k))\\ &=&\delta_t+\gamma\lambda\delta_{t+1}+(\gamma\lambda)^2\delta_{t+2}+\cdots\tag{12.2} \end{eqnarray*} \]

与第九章\(w_{TD}\)的稳定点一样，离线\(\lambda\)-回报算法的稳定点在于\(G_t^\lambda-\hat{v}(S_t,w_t)=0\)。根据算法渐进稳定性质，式（12.2）中\(\delta_{t+i}\approx\overline{VE}(w_\infin)\)，可得

\[\overline{VE}(w_{TD})\approx\frac{1}{1-\gamma\lambda}\overline{VE}(w_\infin) \]

结合第九章的收敛性结果，

\[\overline{\text{VE}}(w_{\text{TD}})\leq\frac{1}{1-\gamma}\min_w\overline{\text{VE}}(w) \]

可得

\[\overline{VE}(w_\infin)\leq\frac{1-\gamma\lambda}{1-\gamma}\min_w\overline{VE}(w) \]

证明完毕。

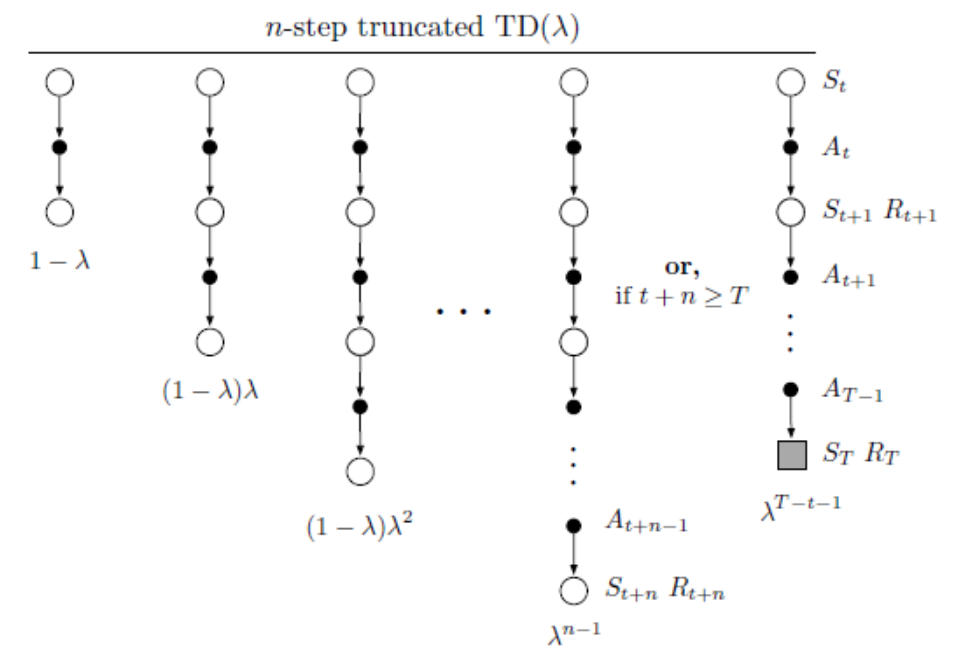
4. \(n\)步截断\(\lambda\)-回报算法

\(n\)步截断\(\lambda\)-回报算法，是对离线\(\lambda\)-回报算法的一种改进，融入了TD算法的思想，不必等到一轮交互完成后才进行更新，但不引入有效循迹方法，故而为区别TD(\(\lambda\))算法，称为TTD(\(\lambda\))算法（截断TD(\(\lambda\))）。定义截断\(\lambda\)-回报为

\[\begin{eqnarray*} G_{t:h}^\lambda&=&(1-\lambda)\sum_{n=1}^{h-t-1}\lambda^{n-1}G_{t:t+n}+\lambda^{h-t-1}G_{t:h},\ 0\leq t<h\leq T\\ &=&R_{t+1}+\gamma\lambda G_{t+1}^\lambda+\gamma(1-\lambda)\hat{v}(S_{t+1},w) \end{eqnarray*} \]

截断\(\lambda\)-回报的递推表达式推导起来比式（12.1）稍微复杂一些，下面给出大概的证明（会跳步）：

\[\begin{eqnarray*} G_{t:h}^\lambda &=& R_{t+1}+\gamma(1-\lambda)\sum_{n=1}^{h-t-1}\lambda^{n-1}G_{t+1:t+n}+\gamma\lambda^{h-t-1}G_{t+1:h}\\ &=&R_{t+1}+\gamma(1-\lambda)\hat{v}(S_{t+1},w)+\gamma\lambda(1-\lambda)\sum_{n=1}^{h-t-2}\lambda^{n-1}G_{t+1:t+n+1}+\gamma\lambda\lambda^{h-t-2}G_{t+1:h}\\ &=&R_{t+1}+\gamma\lambda G_{t+1:h}^\lambda+\gamma(1-\lambda)\hat{v}(S_{t+1},w)\\ &=& R_{t+1}+\gamma[(1-\lambda)\hat{v}(S_{t+1},w)+\lambda G_{t+1:h}^\lambda] \end{eqnarray*} \]

证明完成。从最后的式子可以看出，下一时刻的状态价值估计本质上是\(\lambda\)-回报与价值估计的加权和。

根据截断\(\lambda\)-回报可得TTD(\(\lambda\))算法的更新式为

\[w_{t+n}=w_{t+n-1}+\alpha[G_{t:t+n}^\lambda-\hat{v}(S_t,w_{t+n-1})]\nabla\hat{v}(S_k,w_{t+n-1}),\ 0\leq t<T \]

更新式的后备图如下图所示。

截断\(\lambda\)-回报\(G_{t:t+k}^\lambda\)也可以写成

\[G_{t:t+k}^\lambda=\hat{v}(S_t,w_{t-1})+\sum_{i=t}^{t+k-1}(\gamma\lambda)^{i-t}\delta'_i \]

其中，\(\delta_t'=R_{t+1}+\gamma\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t)\)。该式的证明比较简单，根据式（12.2）可得

\[\begin{eqnarray*} G_{t:t+k}^\lambda-\hat{v}(S_t,w_{t-1}) &=&\delta_t+\gamma\lambda\delta_{t+1}+(\gamma\lambda)^2\delta_{t+2}+\cdots+(\gamma\lambda)^{k-1}\delta_{t+k-1} \end{eqnarray*} \]

证明完毕。

TTD(\(\lambda\))算法采用传统的TD更新式，只是将目标价值用截断\(\lambda\)-回报代替，未引入有效循迹。

5. 计划更新：在线\(\lambda\)-回报算法

截断\(\lambda\)-回报算法需要选择合适的\(n\)值，当\(n\)值较大时，类似于离线\(\lambda\)-回报算法，但是响应速度较慢。当\(n\)选择较小的时候，类似于TD算法，但每个数据只使用一次，数据的利用效率不高。为了综合两者的优势，采用改进方式为在每次交互后，根据交互轨迹从开始时刻重新计算目标价值进行更新。例如，首次交互时得到交互轨迹\(\{S_0,R_1,S_1\}\)，计算截断\(\lambda\)-回报\(G_{0:1}^\lambda\)进行更新；2次交互时得到交互轨迹\(\{S_0,R_1,S_1,R_2,S_2\}\)，分别计算截断\(\lambda\)-回报\(G_{0:2}^\lambda\)和\(G_{1:2}^\lambda\)进行更新；3次交互时得到交互轨迹\(\{S_0,R_1,S_1,R_2,S_2,R_3,S_3\}\)，分别计算截断\(\lambda\)-回报\(G_{0:3}^\lambda\)、\(G_{1:3}^\lambda\)和\(G_{2:3}^\lambda\)进行更新。具体方法如下所示：

\[\begin{eqnarray*} \begin{array}{l} h=1: && w_1^1=w_0^1+\alpha[G_{0:1}^\lambda-\hat{v}(S_0,w_0^1)]\nabla\hat{v}(S_0,w_0^1),\\ h=2: && w_1^2=w_0^2+\alpha[G_{0:2}^\lambda-\hat{v}(S_0,w_0^2)]\nabla\hat{v}(S_0,w_0^2),\\ && w_2^2=w_1^2+\alpha[G_{1:2}^\lambda-\hat{v}(S_1,w_1^2)]\nabla\hat{v}(S_1,w_1^2),\\ h=3: && w_1^3=w_0^3+\alpha[G_{0:3}^\lambda-\hat{v}(S_0,w_0^3)]\nabla\hat{v}(S_0,w_0^3),\\ && w_2^3=w_1^3+\alpha[G_{1:3}^\lambda-\hat{v}(S_1,w_1^3)]\nabla\hat{v}(S_1,w_1^3),\\ && w_3^3=w_2^3+\alpha[G_{2:3}^\lambda-\hat{v}(S_2,w_2^3)]\nabla\hat{v}(S_2,w_2^3) \end{array} \end{eqnarray*} \]

此处需要注意的是，在更新过程中，每次截断\(\lambda\)-回报的计算都是基于最新的参数估计\(w\)。总结可得其一般表达式为

\[\begin{eqnarray*} w_{t+1}^h &=& w_t^h+\alpha[G_{t:h}^\lambda-\hat{v}(S_t,w_t^h)]\nabla\hat{v}(S_t,w_t^h),\ 0\leq t<h\leq T,\\ G_{t:h}^\lambda &=& (1-\lambda)\sum_{n=1}^{h-t-1}\lambda^{n-1}G_{t:t+n}+\lambda^{h-t-1}G_{t:h} \end{eqnarray*} \]

该方法被称为在线\(\lambda\)-回报算法，相比于离线\(\lambda\)-回报算法，它在每一次交互后都会进行参数更新，具有实时响应的能力，其缺点在于计算复杂度更高，但效果也会更好。尤其是在数据不足的情况下，数据的利用效率较高。

在线\(\lambda\)-回报算法相比TTD(\(\lambda\))算法，区别在于能够重复利用已采集的数据，此处也并未显式的引入有效循迹。

6. 真在线TD(\(\lambda\))算法

上一节介绍的在线\(\lambda\)-回报算法随着交互次数的不断增加，每次参数更新的次数也会相应的呈线性增长趋势，如下图所示。

在某些特殊情况下，如线性函数拟合\(\hat{v}(s,w)=w^\Tau x(s)\)，通过推导可以直接得到从\(w_0^h\)到\(w_h^h\)的更新公式，从而获得真正意义上的在线算法：

\[\begin{eqnarray*} w_{t+1} &=& w_t+\alpha\delta_tz_t+\alpha(w_t^\Tau x_t-w_{t-1}^\Tau x_t)(z_t-x_t),\tag{12.3}\\ z_t &=& \gamma\lambda z_{t-1}+(1-\alpha\gamma\lambda z_{t-1}^\Tau x_t)x_t,\tag{12.4} \end{eqnarray*} \]

其中，\(\alpha, \gamma, \lambda\)分别为学习率、折扣系数和回报权重，\(\delta_t = R_{t+1}+\gamma\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t)\)为状态价值估计误差，\(x_t=x(S_t)\)为状态特征，\(z_t\)为有效循迹（也称为荷兰循迹，dutch trace），但区别于前面所提的有效循迹。下文会给出式（12.3）--（12.4）在蒙特卡洛学习下的推导方式，更具体的过程可以参考论文 “van Seijen, H. (2016). Effective multi-step temporal-difference learning for non-linear function approximation. ArXiv:1608.05151”。 值得注意的是，此处的荷兰循迹同样是后向视角的一种策略，但并非人为设置的，而是计划更新策略下所隐含的。上述的更新式的前置条件是采用线性函数拟合，若采用非线性函数拟合则只能回归到第5节所介绍的方法。后向视角的策略根植于参数\(w_t^h\)的横向更新过程中。

综上所述，可得真在线TD(\(\lambda\))算法具体实现的伪代码，如下图所示。具体代码实现和算法效果可以参考实验1。

为了与第3节TD(\(\lambda\))算法所采用的有效循迹做区分，本节的有效循迹称为荷兰循迹。TD(\(\lambda\))算法使用的有效循迹称为累积循迹（accumulating trace），原因在于\(z_t=\gamma\lambda z_{t-1}+\nabla\hat{v}(S_t,w_t)\)是将每次更新的梯度方向乘一个衰减系数累积起来。当线性函数拟合采用瓦片编码时，因为其状态特征为二值向量，每次更新只需要替换二值向量中为1的元素所对应的参数\(w_{i,t}\)，因此该有效循迹也称为替换循迹（replacing trace），即

\[z_{i,t}=\left\{ \begin{array}{l} 1, && \text{if}\ x_{i,t}=1\\ \gamma\lambda z_{i,t-1}, && \text{otherwise} \end{array} \right. \]

由此可以看出，替换循迹是荷兰循迹的一种特例。一般来说，累积循迹主要应用于非线性拟合的情况。

下面对荷兰循迹在蒙特卡洛（MC）算法中的应用进行理论分析，从中也能看出式(12.3)--(12.4)的部分推导过程。回顾一下MC算法的参数更新式为

\[w_{t+1}=w_t+\alpha[G-w_t^\Tau x_t]x_t,\quad 0\leq t<T. \]

之所以选择MC算法，是因为它更加简单。首先，MC算法的更新只发生在到达终止状态之后，因此，目标价值\(G\)为标量。其次，假设折扣系数\(\gamma=1\)，交互过程中\(R=0\)，仅在最后才获得奖励。我们将最后一次更新的计算量，分摊到每一次交互之后，即

\[\begin{eqnarray*} w_T&=&w_{T-1}+\alpha(G-w_{T-1}^\Tau x_{T-1})x_{T-1}\\ &=&(I-\alpha x_{T-1}x_{T-1}^\Tau)w_{T-1}+\alpha Gx_{T-1}. \end{eqnarray*} \]

定义\(F_t=(I-\alpha x_tx_t^\Tau)\)，进一步可得

\[\begin{eqnarray*} w_T&=&F_{T-1}(F_{T-2}w_{T-2}+\alpha Gx_{T-2})+\alpha G x_{T-1}\\ &=&F_{T-1}F_{T-2}w_{T-2}+\alpha G(F_{T-1}x_{T-2}+x_{T-1})\\ &\vdots&\\ &=&\underbrace{F_{T-1}F_{T-2}\cdots F_0w_0}_{a_{T-1}}+\alpha G\underbrace{\sum_{k=0}^{T-1}F_{T-1}F_{T-2}\cdots F_{k+1}x_k}_{z_{T-1}}\\ &=&a_{T-1}+\alpha Gz_{T-1} \end{eqnarray*} \]

通过上式可得，只要在每次交互之后更新向量\(a_t\)和\(z_t\)，最后得到回报\(G\)就可以完成参数向量\(w\)的更新。向量\(z_t\)就是荷兰循迹，可得其递推形式为

\[\begin{eqnarray*} z_t &=& \sum_{k=0}^tF_tF_{t-1}\cdots F_{k+1}x_k\\ &=&F_t\sum_{k=0}^{t-1}F_{t-1}F_{t-2}\cdots F_{k+1}x_k+x_t\\ &=&F_tz_{t-1}+x_t\\ &&代入F_t，整理可得\\ &=&z_{t-1}-\alpha x_tx_t^\Tau z_{t-1}+x_t\\ &=&z_{t-1}+(1-\alpha z_{t-1}^\Tau x_t)x_t \end{eqnarray*} \]

对比式（12.4），等价于\(\gamma=\lambda=1\)，与第1节对\(\lambda\)的分析是一致的。向量\(a_t\)的递推形式较为简单，即

\[a_t=F_tF_{t-1}\cdots F_0w_0=F_ta_{t-1}=a_{t-1}-\alpha x_tx_t^\Tau a_{t-1}, \]

其中，\(a_0=w_0\)。

7.Sarsa(\(\lambda\))算法

可以将TD(\(\lambda\))算法扩展到Sarsa(\(\lambda\))算法，即将状态价值函数扩展为动作价值函数（状态-动作价值函数），可得其更新式为

\[\begin{eqnarray*} w_{t+1} &=& w_t+\alpha\delta_tz_t,\\ z_t &=& \gamma\lambda z_{t-1}+\nabla\hat{q}(S_t,A_t,w_t),\quad z_{-1}=0, \end{eqnarray*} \]

其中，动作价值误差\(\delta_t = R_{t+1}+\gamma\hat{q}(S_{t+1},A_{t+1},w_t)-\hat{q}(S_t,A_t,w_t)\)。其备份图如下图所示。

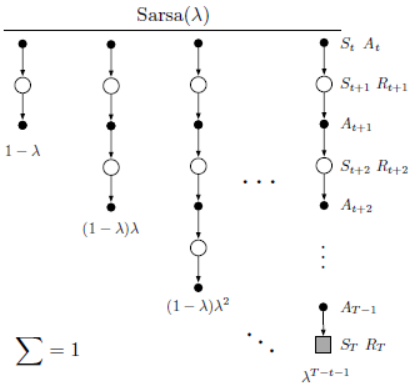
下面给出基于瓦片编码的Sarsa(\(\lambda\))算法的伪代码实现过程，如下图所示。

下面给出有效循迹之所以可以提高算法的学习效率的直观解释。假设在一个网格世界中生成了一段轨迹，初始动作价值估计为零，除到达标记的目标位置G获得正奖励外，其他交互的奖励为零。不同算法下的状态价值变化轨迹如下图所示。

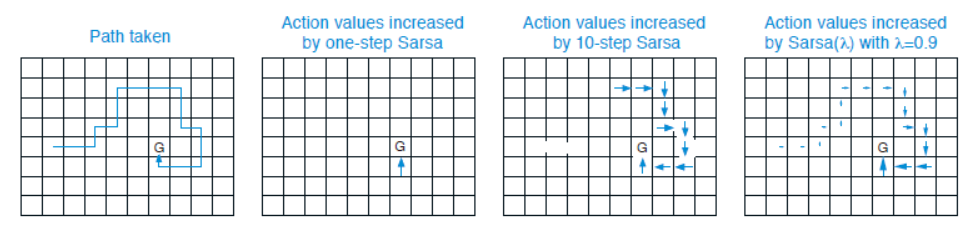
第一张图显示了智能体在一轮交互中的轨迹。其他图片的箭头显示了，当智能体达到目标时，哪些动作价值会增加，以及增加多少。Sarsa算法将只增加最后一个动作价值，而Sarsa(\(n\))算法会同等地增加最后\(n\)个动作的价值。Sarsa(\(\lambda\))算法将更新所有的动作价值，但是按照不同的权重，随着时间的延伸而逐渐衰减。通常衰落策略的效果是最好的。

当然，真在线TD(\(\lambda\))算法也可以扩展为真Sarsa(\(\lambda\))算法，其伪代码如下图所示。

8. \(\lambda\)-回报的一般形式

前面将折扣系数\(\gamma\)和权重\(\lambda\)定义为常量，在本节考虑更为一般的形式，将\(\gamma\)和\(\lambda\)作为函数：

\[\gamma_t=\gamma(S_t),\ \lambda_t=\lambda(S_t,A_t). \]

由此可以得到\(t\)时刻回报的一般表达为

\[\begin{eqnarray*} G_t &=& R_{t+1} + \gamma_{t+1}G_{t+1}\\ &=& R_{t+1} + \gamma_{t+1}R_{t+2}+\gamma_{t+1}\gamma_{t+2}R_{t+3}+\cdots\\ &=&\sum_{k=t}^\infin\left(\prod_{i=t+1}^k\gamma_i\right)R_{k+1} \end{eqnarray*} \]

根据第1节的\(\lambda\)-回报，可得广义\(\lambda\)-回报的递推表达式为

\[G_t^{\lambda s}=R_{t+1}+\gamma_{t+1}[(1-\lambda_{t+1})\hat{v}(S_{t+1},w_t)+\lambda_{t+1}G_{t+1}^{\lambda s}], \]

此处上标增加字符's'表示回报自举采用的是状态价值估计。若上标为'a'表示回报自举采用的是动作价值函数，即

\[G_t^{\lambda a}=R_{t+1}+\gamma_{t+1}[(1-\lambda_{t+1})\hat{q}(S_{t+1},A_{t+1},w_t)+\lambda_{t+1}G_{t+1}^{\lambda a}]. \]

当然，动作价值估计也可以采用期望的形式：

\[\begin{eqnarray*} G_t^{\lambda a}&=&R_{t+1}+\gamma_{t+1}[(1-\lambda_{t+1})\bar{Q}(S_{t+1},w_t)+\lambda_{t+1}G_{t+1}^{\lambda a}],\\ \bar{Q}(S_{t+1},w_t)&=&\sum_a\pi(a|S_{t+1})\hat{q}(S_{t+1},a,w_t). \end{eqnarray*} \]

9.基于控制变量的离线策略有效循迹

根据第7章第4节，结合重要性采样和控制变量可得\(\lambda\)-回报的递推式为

\[G_t^{\lambda s}=\rho_t\left(R_{t+1}+\gamma_{t+1}[(1-\lambda_{t+1})\hat{v}(S_{t+1},w_t)+\lambda_{t+1}G_{t+1}^{\lambda s}]\right)+(1-\rho_t)\hat{v}(S_t,w_t), \]

其中，\(\rho_t=\frac{\pi(A_t|S_t)}{b(A_t|S_t)}\)。根据第4节截断\(\lambda\)-回报的完成式：

\[G_{t:t+k}^\lambda=\hat{v}(S_t,w_{t-1})+\sum_{i=t}^{t+k-1}(\gamma\lambda)^{i-t}\delta'_i, \]

可得离线策略下的，\(G_t^{\lambda s}\)的完成式为

\[G_t^{\lambda s}\approx\hat{v}(S_t,w_t)+\rho_t\sum_{k=t}^\infin\delta_k^s\prod_{i=t+1}^k\gamma_i\lambda_i\rho_i, \]

其中，TD误差\(\delta_t^s=R_{t+1}+\gamma_{t+1}\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t)\)。将\(G_t^{\lambda s}\)代入TD算法的更新式中可得

\[\begin{eqnarray*} w_{t+1}&=&w_t+\alpha(G_t^{\lambda s}-\hat{v}(S_t,w_t))\nabla\hat{v}(S_t,w_t)\\ &\approx& w_t+\alpha\rho_t\left(\sum_{k=t}^\infin\delta_k^s\prod_{i=t+1}^k\gamma_i\lambda_i\rho_i\right)\nabla\hat{v}(S_t,w_t). \end{eqnarray*} \]

从上式可以看出这是一种前向更新方式，不断从各个时刻开始向前计算TD误差。但是乘积项\(\prod_{i=t+1}^k\gamma_i\lambda_i\rho_i\)像是一种有效循迹（对照\(\alpha\delta_tz_t\)）。下面给出其隐含有效循迹的证明：

\[\begin{eqnarray*} w_\infin-w_t&=&\sum_{t=1}^\infin (w_{t+1}-w_t)\\ &\approx& \sum_{t=1}^\infin\sum_{k=t}^\infin\alpha\rho_t\delta_k^s\nabla\hat{v}(S_t,w_t)\prod_{i=t+1}^k\gamma_i\lambda_i\rho_i\\ &&利用累加规则\ \sum_{t=x}^y\sum_{k=t}^y = \sum_{k=x}^y\sum_{t=x}^k\\ &=&\sum_{k=1}^\infin\alpha\delta_k^s\sum_{t=1}^k\rho_t\nabla\hat{v}(S_t,w_t)\prod_{i=t+1}^k\gamma_i\lambda_i\rho_i, \end{eqnarray*} \]

上式中第二项累加和就是一种后向视角，具体可得

\[\begin{eqnarray*} z_k&=&\sum_{t=1}^k\rho_t\nabla\hat{v}(S_t,w_t)\prod_{i=t+1}^k\gamma_i\lambda_i\rho_i\\ &=&\sum_{t=1}^{k-1}\rho_t\nabla\hat{v}(S_t,w_t)\prod_{i=t+1}^k\gamma_i\lambda_i\rho_i+\rho_k\nabla\hat{v}(S_k,w_k)\\ &=&\gamma_k\lambda_k\rho_k\sum_{t=1}^{k-1}\rho_t\nabla\hat{v}(S_t,w_t)\prod_{i=t+1}^{k-1}\gamma_i\lambda_i\rho_i+\rho_k\nabla\hat{v}(S_k,w_k)\\ &=&\rho_k(\gamma_k\lambda_kz_{k-1}+\nabla\hat{v}(S_k,w_k)) \end{eqnarray*} \]

总结可得，\(z_t=\rho_t(\gamma_t\lambda_tz_{t-1}+\nabla\hat{v}(S_t,w_t))\)，这是累积循迹。同理可以将\(G_t^{\lambda s}\)扩展到\(G_t^{\lambda a}\)，这里就不再赘述了。TD(\(\lambda\))算法是一种在线算法，相当于\(\rho_t=1\)（因为目标策略等同于交互策略），因此可以看作是离线策略的一种特例。值得注意的是，在上述证明中\(z_t\)的估计都是基于参数估计\(w_t\)，相当于离线算法只在最后一次交互时才进行参数更新，但可以将计算量分摊至之前的每一次交互。当\(\lambda=1\)，\(\lambda\)-回报离线算法等价于蒙特卡洛算法，上述讨论与之相同。当\(\lambda<1\)，此时需要注意死亡三元素，\(\lambda\)-回报离线算法适用于列表法，但不适合于函数近似法。

10. Watkins's \(Q(\lambda)\)到树备份（TB(\(\lambda\))）算法

有一些方法可以将有效循迹应用到Q-learning方法中。最初的方法便是Watkins's Q(\(\lambda\))算法，当交互轨迹为一连串的贪婪动作时，有效循迹与TD(\(\lambda\))算法中的一样随着交互的增加而逐步衰减。但是当动作为非贪婪动作时，有效循迹则被设置为0，即累积循迹遇到非贪婪动作时则停止累积。Q(\(\lambda\))算法的备份图如下图所示。

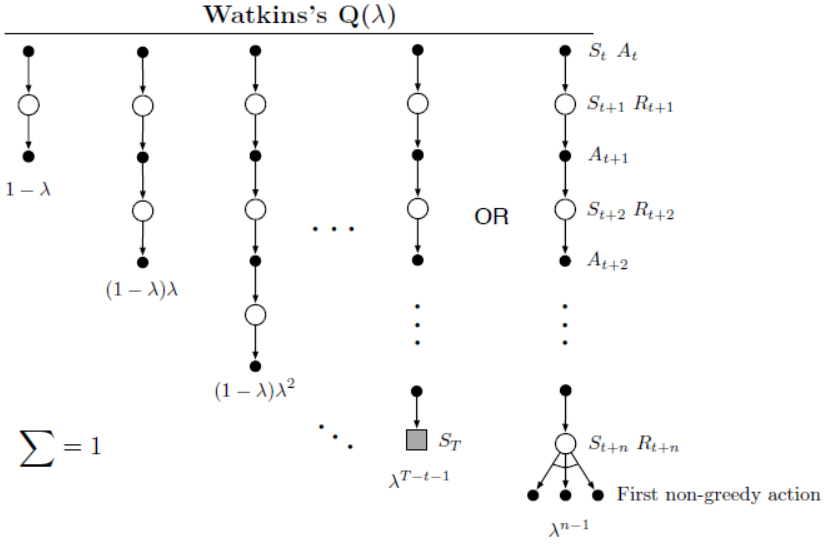
Q-learing算法是一种较为特殊的离线策略算法。与之相比，树备份算法是一种离线策略算法且不需要引入重要性采样。将有效循迹应用到树备份算法，也称为TB(\(\lambda\))算法。其备份图如下图所示。

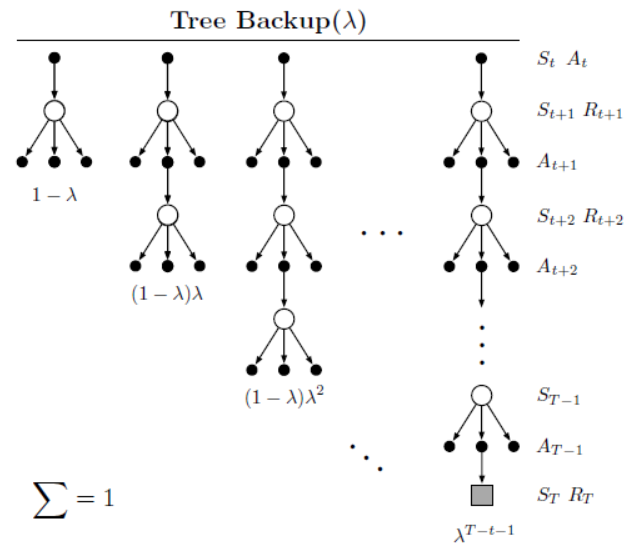
根据第8节中的广义\(\lambda\)-回报的递推表达式，可得树备份算法下的\(\lambda\)-回报的递推式为

\[\begin{eqnarray*} G^{\lambda a}_t &=& R_{t+1}+\gamma_{t+1}\left((1-\lambda_{t+1})\bar{Q}(S_{t+1},w_t)+\lambda_{t+1}(\sum_{a\neq A_{t+1}}\pi(a|S_{t+1})\hat{q}(S_{t+1},a,w_t)+\pi(A_{t+1}|S_{t+1})G_{t+1}^{\lambda a})\right)\\ &=&R_{t+1}+\gamma_{t+1}\left(\bar{Q}(S_{t+1},w_t)+\lambda_{t+1}\pi(A_{t+1}|S_{t+1})(G_{t+1}^{\lambda a}-\hat{q}(S_{t+1},A_{t+1},w_t))\right) \end{eqnarray*} \]

根据第2节式（12.2）的推导，类比可得\(G_t^{\lambda a}\)的一次完成式，

\[G_t^{\lambda a}\approx\hat{q}(S_t,A_t,w_t)+\sum_{k=t}^\infin\delta_k^a\prod_{i=t+1}^k\gamma_i\lambda_i\pi(A_i|S_i), \]

其中，TD误差\(\delta_k^a=R_{t+1}+\gamma_{t+1}\bar{Q}(S_{t+1},w_t)-\hat{q}(S_t,A_t,w_t)\)。

参照第9节的推导，可得TB(\(\lambda\))算法中隐含的有效循迹：

\[z_t=\gamma_t\lambda_t\pi(A_t|S_t)z_{t-1}+\nabla\hat{q}(S_t,A_t,w_t) \]

跟其他的半梯度算法相同，TB(\(\lambda\))算法在死亡三要素的情况下也不能保证稳定与收敛。

11.基于有效循迹的稳定离线方法

在第11章中介绍了真正意义上的随机梯度算法GTD算法，在实际应用过程中会引入辅助向量\(v_t\)，得到真正可以使用的TDC算法。将有效循迹应用于TDC算法，称为TDC(\(\lambda\))算法。需要注意的是，TDC算法的整个实现过程是基于线性函数拟合的，对于非线性函数则不适用。下面直接给出TDC(\(\lambda\))算法参数更新公式为

\[\begin{eqnarray*} w_{t+1}&=&w_t+\alpha\delta_t^sz_t-\alpha\gamma_{t+1}(1-\lambda_{t+1})(z_t^\Tau v_t)x_{t+1},\\ v_{t+1}&=&v_t+\beta\delta_t^sz_t-\beta(v_t^\Tau x_t)x_t, \end{eqnarray*} \]

其中，TD误差\(\delta_t^s=R_{t+1}+\gamma_{t+1}\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t)\)，有效循迹\(z_t=\rho_t(\gamma_t\lambda_tz_{t-1}+\nabla\hat{v}(S_t,w_t))\)。这里需要说明，该更新公式博主并未进行推理确认，比较好奇为何会出现\((1-\lambda_{t+1})\)这一项。后面有精力了会将证明补上。

TDC(\(\lambda\))算法考虑的是状态价值，将其思想扩展到动作价值可得GQ(\(\lambda\))算法。其目标在于学习动作价值函数\(\hat{q}(s,a,w_t)=w_t^\Tau x(s,a)\approx q_\pi(s,a)\)。当目标策略采用\(\epsilon\)-greedy策略或是贪婪策略时，GQ(\(\lambda\))算法可以作为控制算法。其参数更新公式为

\[\begin{eqnarray*} w_{t+1}&=&w_t+\alpha\delta_t^az_t-\alpha\gamma_{t+1}(1-\lambda_{t+1})(z_t^\Tau v_t)\bar{x}_{t+1},\\ v_{t+1}&=&v_t+\beta\delta_t^az_t-\beta(v_t^\Tau x_t)x_t,\\ z_t &=& \gamma_t\lambda_t\rho_tz_{t-1}+\nabla\hat{q}(S_t,A_t,w_t), \end{eqnarray*} \]

其中，

\[\begin{eqnarray*} \bar{x}_t &=& \sum_a\pi(a|S_t)x(S_t,a),\\ \delta_t^a &=& R_{t+1}+\gamma_{t+1}w_t^\Tau\bar{x}_{t+1}-w_t^\Tau x_t. \end{eqnarray*} \]

下面将GTD(\(\lambda\))和TD(\(\lambda\))相结合，TD(\(\lambda\))更为简单快速，但GTD(\(\lambda\))是真正意义上的随机梯度算法，具有无偏稳定的特点，两者相结合称之为HTD(\(\lambda\))（hybrid TD）算法：

\[\begin{eqnarray*} w_{t+1}&=&w_t+\alpha\delta_t^sz_t+\alpha\left((z_t-z_t^b)^\Tau v_t\right)(x_t-\gamma_{t+1}x_{t+1}),\\ v_{t+1}&=&v_t+\beta\delta_t^sz_t-\beta({z_t^b}^\Tau v_t)(x_t-\gamma_{t+1}x_{t+1}),\ \text{with}\ v_0=0,\\ z_t&=&\rho_t(\gamma_t\lambda_tz_{t-1}+x_t),\ \text{with}\ z_{-1}=0,\\ z_t^b&=&\gamma_t\lambda_tz_{t-1}^b+x_t,\ \text{with}\ z_{-1}^b=0,\\ \end{eqnarray*} \]

此处博主也有疑惑，首先\((1-\lambda_{t+1})\)这项为何不见了，其次两个算法是如何结合的，是基于GTD的原理，然后将TD(\(\lambda\))算法代入到其中的期望项中吗？当然，从算式本身来看，当目标策略与交互策略相同时，算法就退化称为TD(\(\lambda\))算法，这显然是正确的。

最后，将有效循迹扩展至重要性TD算法，得到E-TD(\(\lambda\))算法：

\[\begin{eqnarray*} w_{t+1}&=&w_t+\alpha\delta_tz_t,\\ \delta_t&=&R_{t+1}+\gamma_{t+1}w_t^\Tau x_{t+1}-w_t^\Tau x_t,\\ z_t &=&\rho_t(\gamma_t\lambda_tz_{t-1}+M_tx_t),\\ M_t &=&\lambda_tI_t+(1-\lambda_t)F_t,\\ F_t &=& \rho_{t-1}\gamma_tF_{t-1}+I_t,\quad F_0与状态S_0有关 \end{eqnarray*} \]

这里需要提及的是，有研究论文表明TD(\(\lambda\))算法的收敛性仅在\(\lambda\)为常数的时候才能得到保证。而第11节提到的算法没有这个限制。

12. 小结

本章主要介绍了有效循迹的思想和方法，引入有效循迹的方式有两种，一种是人为设定，例如TD(\(\lambda\))算法；另一种是引入\(\lambda\)-回报或者截断\(\lambda\)-回报，结合计划更新方式或者是其他离线策略算法，使得扩展后的算法中隐含了有效循迹的方式。有效循迹是一种后向视角的策略，它保存了之前交互得到的轨迹信息。这与以往的学习策略有本质区别，以往的学习策略是通过向前预测其状态价值或者动作价值，从而更新参数或是策略。本章后面几小节涉及的算法没有给出相应的推导细节。

12 .实验

实验1：Random Walk问题

考虑一个马尔可夫奖励过程（Markov reward process, MRP），每轮交互都从中心状态开始，每个状态可以随机选择向左或者向右两种动作，两个动作的选择概率为50%。每轮交互的结束状态位于最左端和最右端，当智能体到达最右端获得奖励\(R=+1\)，到达最左端获得奖励\(R=-1\)，其他状态转移的奖励均为\(R=0\)。本次MRP过程共有19个状态，分别利用离线\(\lambda\)-回报算法、TD(\(\lambda\))算法和真在线TD(\(\lambda\))算法估计状态价值，并对比这三个算法性能。

因为实验的MRP过程的状态较少，因此采用状态聚集的线性近似方法，将每个状态作为一类，即状态特征是一个二值向量，每个时刻向量中有且只有一个元素为1，其余元素为0。可得状态价值估计\(v(S_i)=w^\Tau x(S_i)=w_i\)。

对于离线\(\lambda\)-回报算法，其核心公式为

\[\begin{eqnarray*} G_t^\lambda&=&(1-\lambda)\sum_{n=1}^{T-t-1}\lambda^{n-1}G_{t:t+n}+\lambda^{T-t-1}G_t\\ w_{k+1}&=&w_k+\alpha[G_k^\lambda-\hat{v}(S_k,w_k)]\nabla\hat{v}(S_k,w_k),\ k=0,1,\ldots,T-1 \end{eqnarray*} \]

代码实现过程中，需要先计算\(G_{t:t+n}\)，核心代码如下。

def n_step_return_from_time(self, n, time):
    # gamma=1 仅当到达终止状态奖励才不为0
    end_time = min(time + n, self.T)
    returns = self.value(self.trajectory[end_time])
    if end_time == self.T:
        returns += self.reward
    return returns

然后计算\(G_t^\lambda\)，当交互轨迹较长时，\(\lambda^n\)会特别小对\(\lambda\)-回报的贡献度贡献度可以忽略，因此会添加一个截断阈值来加快计算，核心代码如下。

def lambda_return_from_time(self, time):
    returns = 0.0
    lambda_power = 1
    for n in range(1, self.T - time):
        returns += lambda_power * self.n_step_return_from_time(n, time)
        lambda_power *= self.rate
        if lambda_power < self.rate_truncate:
        # 当系数过小时，则截断
            break
    returns *= 1 - self.rate
    if lambda_power >= self.rate_truncate:
        returns += lambda_power * self.reward
    return returns

参数更新就比较简单了，因为采用的是二值特征，因此每次迭代只需要更新对应状态的权重，核心代码如下。

def off_line_learn(self):
    for time in range(self.T):
        # update for each state in the trajectory
        state = self.trajectory[time]
        delta = self.lambda_return_from_time(time) - self.value(state)
        delta *= self.step_size
        self.weights[state] += delta

在实验过程中，初始参数为\(w=0_{19}\)，\(\alpha\in(0,1]\)，\(\gamma=1\)。\(\lambda\in[0.0, 0.4, 0.8, 0.9, 0.95, 0.975, 0.99, 1]\)。当\(\lambda\)较大时，学习率较大会导致算法发散。考察离线\(\lambda\)-回报算法的瞬时性能，计算状态价值估计与真实状态价值的均方误差，共进行10轮交互。为了保证实验结果的一致性，共进行50轮重复实验。具体代码参照随书代码第12章random_walk.py，实验结果如下图所示。

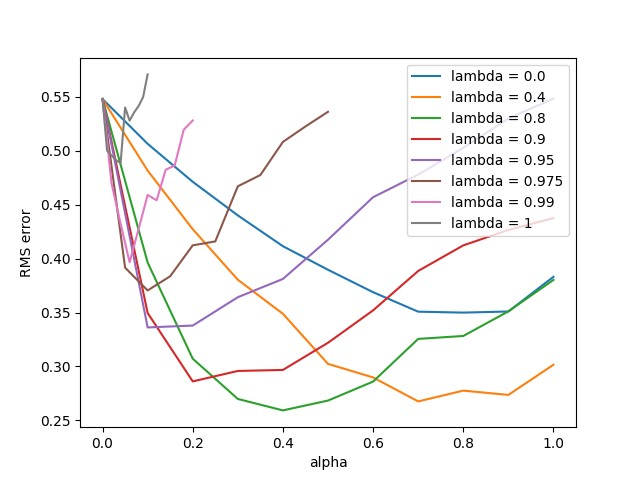
对于TD(\(\lambda\))算法而言，其核心公式为

\[\begin{eqnarray*} w_{t+1}&=&w_t+\alpha\delta_tz_t,\\ z_t&=&\gamma\lambda z_{t-1}+\nabla\hat{v}(S_t,w_t),\\ \delta_t &=& R_{t+1}+\gamma\hat{v}(S_{t+1},w_t)-\hat{v}(S_t,w_t) \end{eqnarray*} \]

与TD(0)算法相比，由于有效循迹的存在，使得每次交互所有状态的权重都会得到更新。实验过程和上述过程保持一致。实验结果如下图所示。

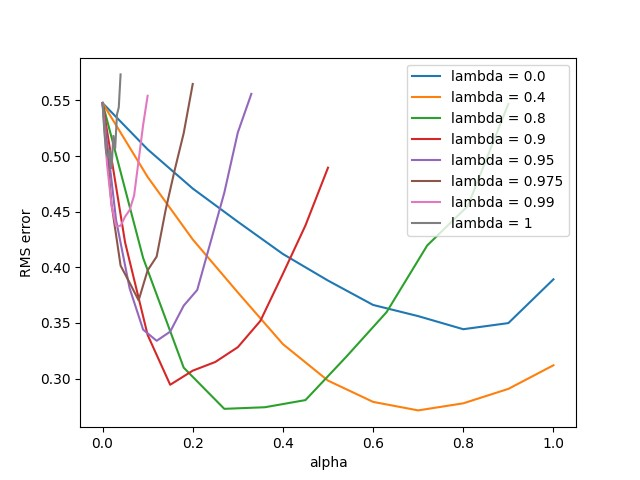
对于真在线TD(\(\lambda\))算法而言，其核心公式为

\[\begin{eqnarray*} w_{t+1} &=& w_t+\alpha\delta_tz_t+\alpha(w_t^\Tau x_t-w_{t-1}^\Tau x_t)(z_t-x_t)\\ &=& w_t + \alpha(\delta_t+V(S_t)-V_{old}(S_t))z_t-\alpha(V(S_t)-V_{old}(S_t))x_t\\ z_t &=& \gamma\lambda z_{t-1}+(1-\alpha\gamma\lambda z_{t-1}^\Tau x_t)x_t,\\ \delta_t&=&R_{t+1}+\gamma V(S_{t+1})-V(S_t). \end{eqnarray*} \]

这里需要注意的是，核心公式中涉及三个状态价值估计，尤其是基于上一时刻的权值估计计算得到的状态价值\(V_{old}(S_t)\)，在代码实现过程中容易搞错。实验过程和上述过程保持一致。实验结果如下图所示。

对比上面三张图，真在线TD(\(\lambda\))算法的算法性能略低于离线\(\lambda\)-回报算法，但是比TD(\(\lambda\))算法要好。原因在于，真在线TD(\(\lambda\))算法是采用自举的方式进行更新，存在有偏估计，但是它能重复利用数据，因此效果的得到了提升。从运算速度方面而言，TD(\(\lambda\))算法是最快的，因为它的计算量小，其次是真在线TD(\(\lambda\))算法。从响应速度方面而言，离线\(\lambda\)-回报算法无法做到实时响应，它需要完成一轮交互之后才能进行更新，因此在实际应用当中有很大限制。真在线TD(\(\lambda\))算法的整体性能更加均衡，在保证响应速度情况下，重复利用数据，提升了性能。最后，附上第七章TD(n)算法的瞬时性能效果图。

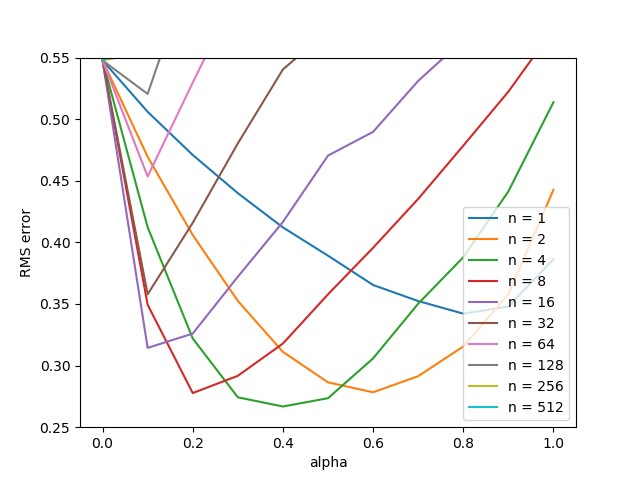
对比可以看出，引入有效循迹之后，算法对学习率的变化不再那么敏感。从算法性能上而言，也是引入有效循迹的算法能好一些。

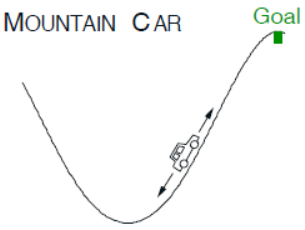
实验2：汽车爬坡任务

实验2 采用与第十章实验1相同的实验环境。这里做简要的描述，考虑驾驶一辆动力不足的汽车沿着陡峭的山路行驶的任务，如下图所示。小车的动作有三种行为\(A_t\)，分别是向前（\(+1\)），向后（\(-1\)）和不踩油门（0）。汽车在达到目标位置之前的每一步的奖励都是\(R=-1\)。

爬坡任务的状态包含汽车的位置\(x_t\)和车速\(\dot{x}_t\)，其更新方式为

\[\begin{eqnarray} x_{t+1}&=&bound[x_t+\dot{x}_{t+1}]\\ \dot{x}_{t+1}&=&bound[\dot{x}_t+force*A_t-gravity*cos(3x_t)] \end{eqnarray} \]

其中，位置范围限制在\([-1.2,0.5]\)和速度范围限制在\([-0.07,0.07]\)。加速系数\(force=0.001\)，重力系数\(gravity=0.0025\)。每一轮游戏开始，小车的速度为0，随机位置\(x_0\in[-0.6,-0.4]\)。采用瓦片编码方式近似动作价值函数，利用Sarsa(\(\lambda\))算法估计最优策略。超参数选择\(\gamma=1\)，瓦片数量\(=8\)，哈希表大小=\(2048\)，学习率\(\alpha=0.3\)。动作选择采用过估计的方式，因此\(\epsilon=0\)。

利用Sarsa(\(\lambda\))算法的核心公式为

\[\begin{eqnarray*} w_{t+1} &=& w_t+\alpha\delta_tz_t,\\ z_t &=& \gamma\lambda z_{t-1}+\nabla\hat{q}(S_t,A_t,w_t),\quad z_{-1}=0, \end{eqnarray*} \]

需要注意的是，核心公式中的有效循迹采用的是累积循迹的效果并不理想。其原因可能在于轨迹采样的有偏性，使得状态空间中的感兴趣区域被不断访问，累积循迹\(z_t\)的某些元素会被不断增强，当更好策略出现时难以进行纠正。后面会针对不同的循迹方式进行比较实验，引入替换循迹、带修正的替换循迹和荷兰循迹。

考察Sarsa(\(\lambda\))算法的瞬时性能，记录每轮游戏的交互次数，共进行50轮交互，最后计算得到每轮游戏平均交互次数。实验采用替换循迹，为了保证实验结果的一致性，共进行100轮重复实验。具体代码参照随书代码第12章mountain_car.py，实验结果如下图所示。

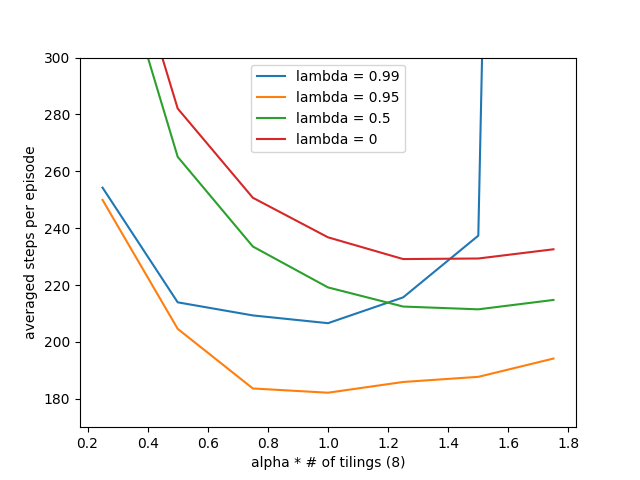
从实验结果可以看出，\(\lambda\)越小Sarsa(\(\lambda\))算法对学习率的敏感度越低，这与第一节的理论分析是一致的。当\(\lambda\)越小，\(\lambda\)-回报就越接近于单步Sarsa回报，而Sarsa(0)算法对学习率的敏感度就比较低，可以参考与第10章的实验1的结果。当\(\lambda\)越大，那么更长轨迹会被纳入考量，这时学习率过大会导致算法不稳定。

下面比较累积循迹、替换循迹、带修正的替换循迹和荷兰循迹的瞬时性能。

• 累积循迹

  核心公式为\(z_t = \gamma\lambda z_{t-1}+\nabla\hat{q}(S_t,A_t,w_t)\)，正如前面所说，轨迹采样存在有偏会导致算法不稳定。当\(\lambda\)取值较小时，纳入考量的轨迹长度也会变小，此时算法就可以稳定了。

• 替换循迹

  核心公式为

  \[z_{i,t}=\left\{ \begin{array}{l} 1, && \text{if}\ x_{i,t}=1\\ \gamma\lambda z_{i,t-1}, && \text{otherwise} \end{array} \right. \]

  替换循迹的好处在于限制了循迹的最大值，从而增强了智能体的探索能力。在本实验中表现也是比较好的。类似的可以扩展到Cart-Pole模型。

• 带修正的替换循迹

  核心公式为

  \[z_{i,t}=\left\{ \begin{array}{l} 1, && \text{if}\ x_{i,t}=1\\ 0, && \text{if}\ x_{i,t}=x_i(S_t,a_t),\ a_t为未被选中的动作\\ \gamma\lambda z_{i,t-1}, && \text{otherwise} \end{array} \right. \]

  将未被选中的动作的循迹进行清空，即将未选中的状态-动作所对应的瓦片编码的循迹设置为0。这里相当于做了一个假设，若动作未被选中则表示该动作不值得加强。当然，这样也有一个缺点，当采用\(\epsilon\)-greedy策略时，贪婪动作可能得不到加强，智能体的探索能力加强了，但是挖掘能力减弱了。在本实验中，带修正的替换循迹的瞬时表现不如替换循迹，这也可以理解，因为前者的挖掘能力相对弱一些，但是更有可能找到最优策略。

• 荷兰循迹

  核心公式为

  \(z_t = \gamma\lambda z_{t-1}+(1-\alpha\gamma\lambda z_{t-1}^\Tau x_t)x_t\)

  荷兰循迹的表现是最好的，在探索和挖掘之间找到了更好平衡。计算量虽然会大一些，但是效果会好很多。不得不说这是一个非常强大的算法，唯一不足在于荷兰循迹是针对线性函数拟合的，不适用于非线性函数拟合。

为了保证实验结果的一致性，共进行50轮重复实验。参数选择\(\lambda=0.95\)，共交互30轮。具体代码参照随书代码第12章mountain_car.py，实验结果如下图所示。

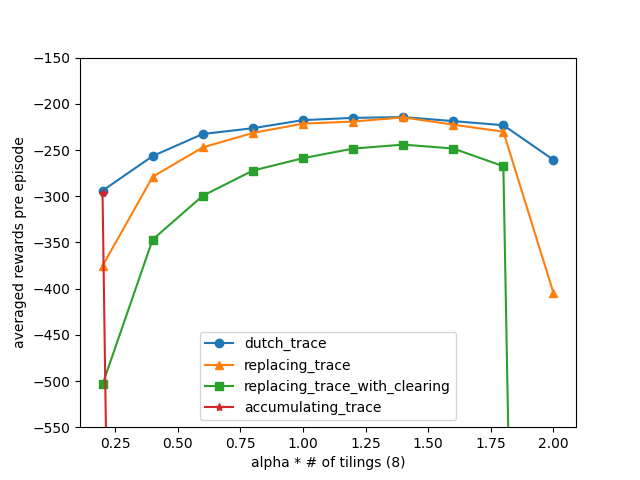
实验结果于上面的分析是一致的。

实验3：有效循迹的优势

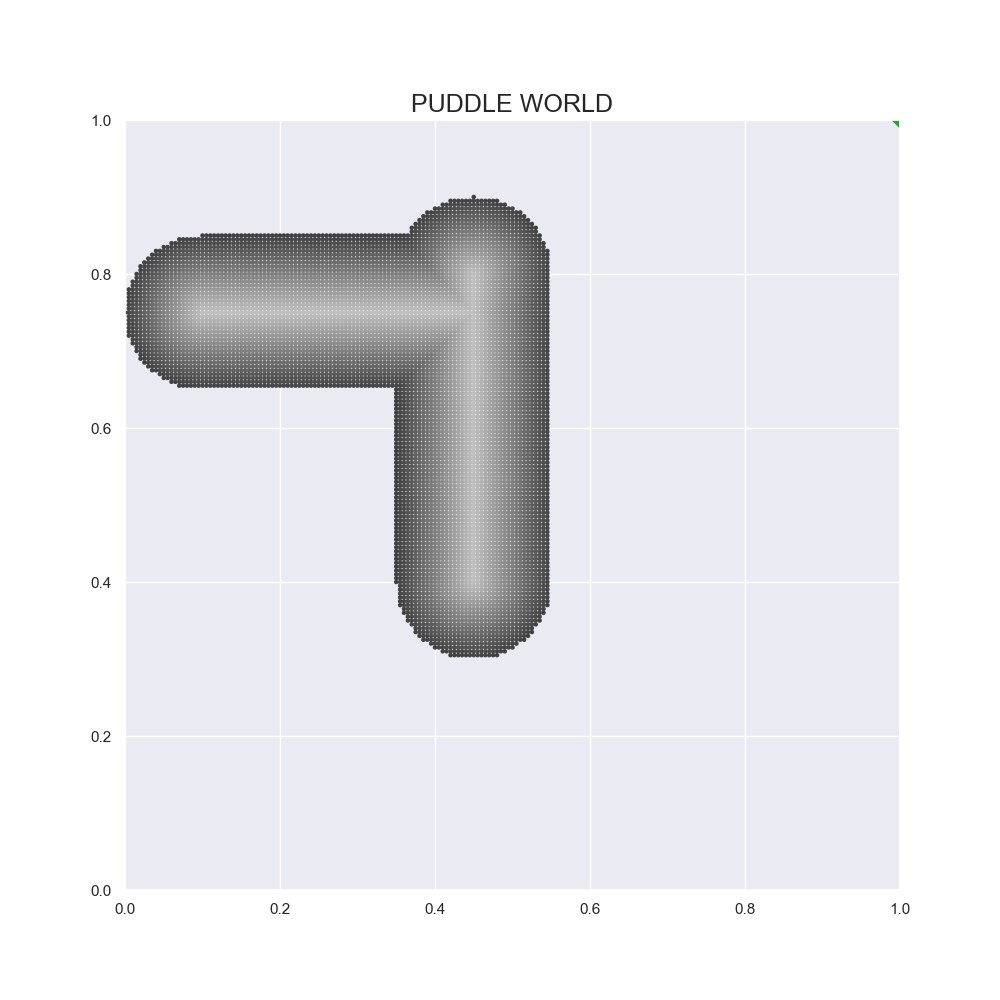
本实验针对四种环境进行有效循迹算法的测试，分别为随机游走任务（参考第九章实验2）、汽车爬坡任务（参考第十章实验1）、Cart-Pole任务和水坑世界任务。其中，水坑世界任务如下图所示，智能体总是从左上角出发寻找一条路径前往右上角。灰色部分为水坑，当智能体踩到水坑时会受到惩罚得到较大的负奖励，负奖励的程度与智能体踩入水坑的程度有关。只要没达到终点，每一次交互的奖励都是\(R=-1\)。

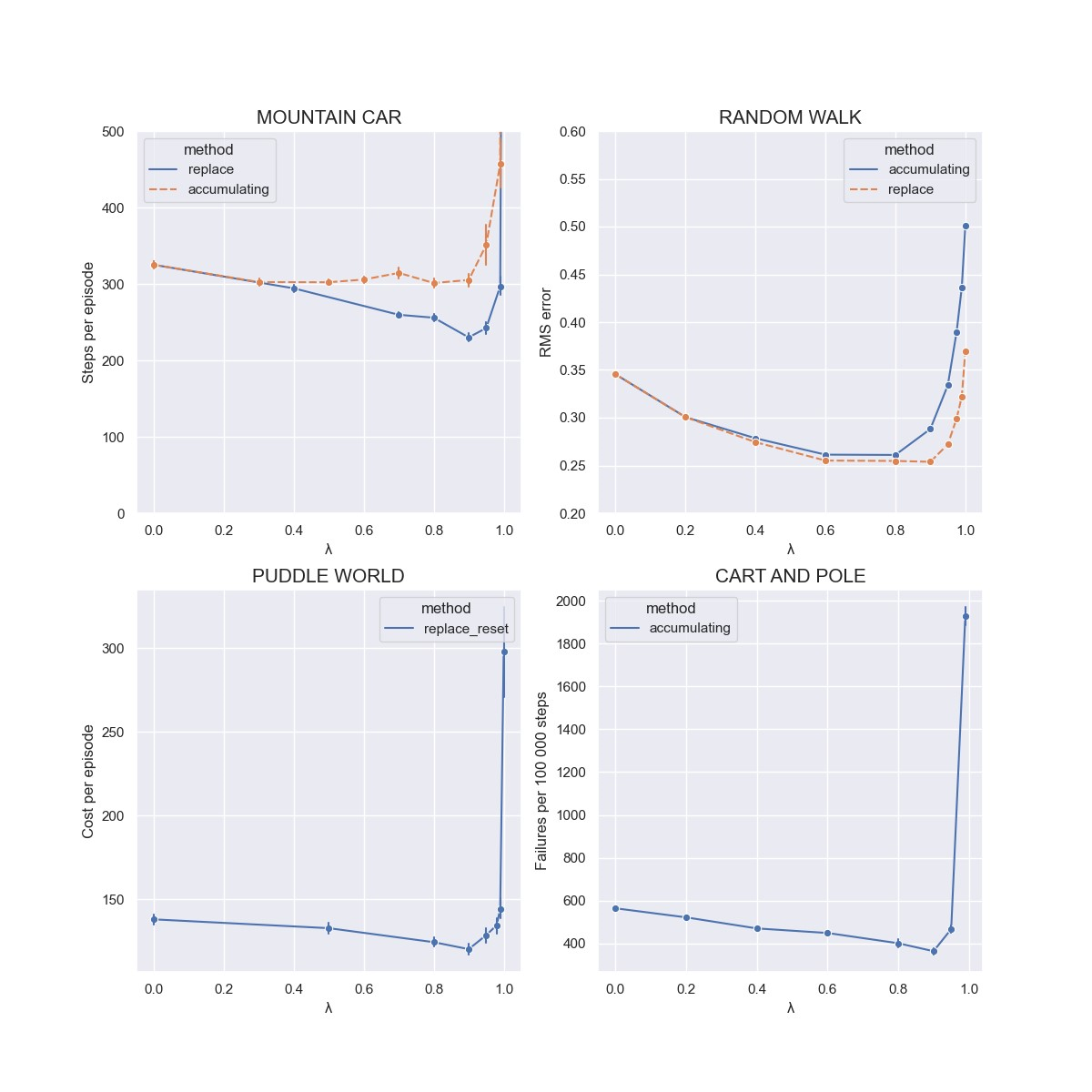
考察有效循迹对TD(\(\lambda\))或Sarsa(\(\lambda\))算法的瞬时性能的影响，不同环境记录的评价指标是不同的，随机游走任务记录的是状态价值估计与真实状态价值的均方误差；汽车爬坡任务记录的是每局的平均交互次数；Cart-Pole任务记录的是在给定最大交互次数内，智能体平均失败次数；水坑世界任务记录的是每局的平均累积奖励。

具体代码参照随书代码第12章lambda_effect.py，代码非常的长，主要将有效循迹的计算部分单独定义出来从而增加代码灵活性，详见函数update_trace_vector。每个环境设置了三个类分别是环境类、智能体类和任务类，例如随机游走任务中RandomWalkEnvironment类用于定义随机游走任务环境；RandomWalkAgent类用于定义智能体及其学习方式run_td_lambda()；RandomWalk类用于定义任务，包括记录数据和训练。

值得一提的是，在记录大量实验数据的过程中，灵活应用pandas库记录不同\(\lambda\)不同有效循迹策略下的评价指标，利用dataframe.groupby()函数实现对不同条件下的评价指标的均值的计算。这个技巧非常有用。

最后，实验结果如下图所示。