强化学习读书笔记 -- 第七章n步自举法

本章将会把蒙特卡洛（Monte Carlo, MC）算法和单步时序差分（one-step temporal-difference, TD(0)）方法相结合。MC算法需要完成一轮交互才进行更新，而TD(0)算法则是每一步都进行更新，两者都比较极端。n步TD算法综合了这两者的特点，它可以允许交互\(n\)次再进行更新。在许多应用中，虽然希望策略更新的速度越快越好以适应环境的任何变化，但是自举方法效果最好的方式往往是隔上一段时间，当一个状态发生显著变化后触发更新。

1. n步TD预测

n步TD算法作为介于TD(0)与MC算法中间的方法，累积一定数量的奖励后更新价值函数。其表现形式如下图所示。

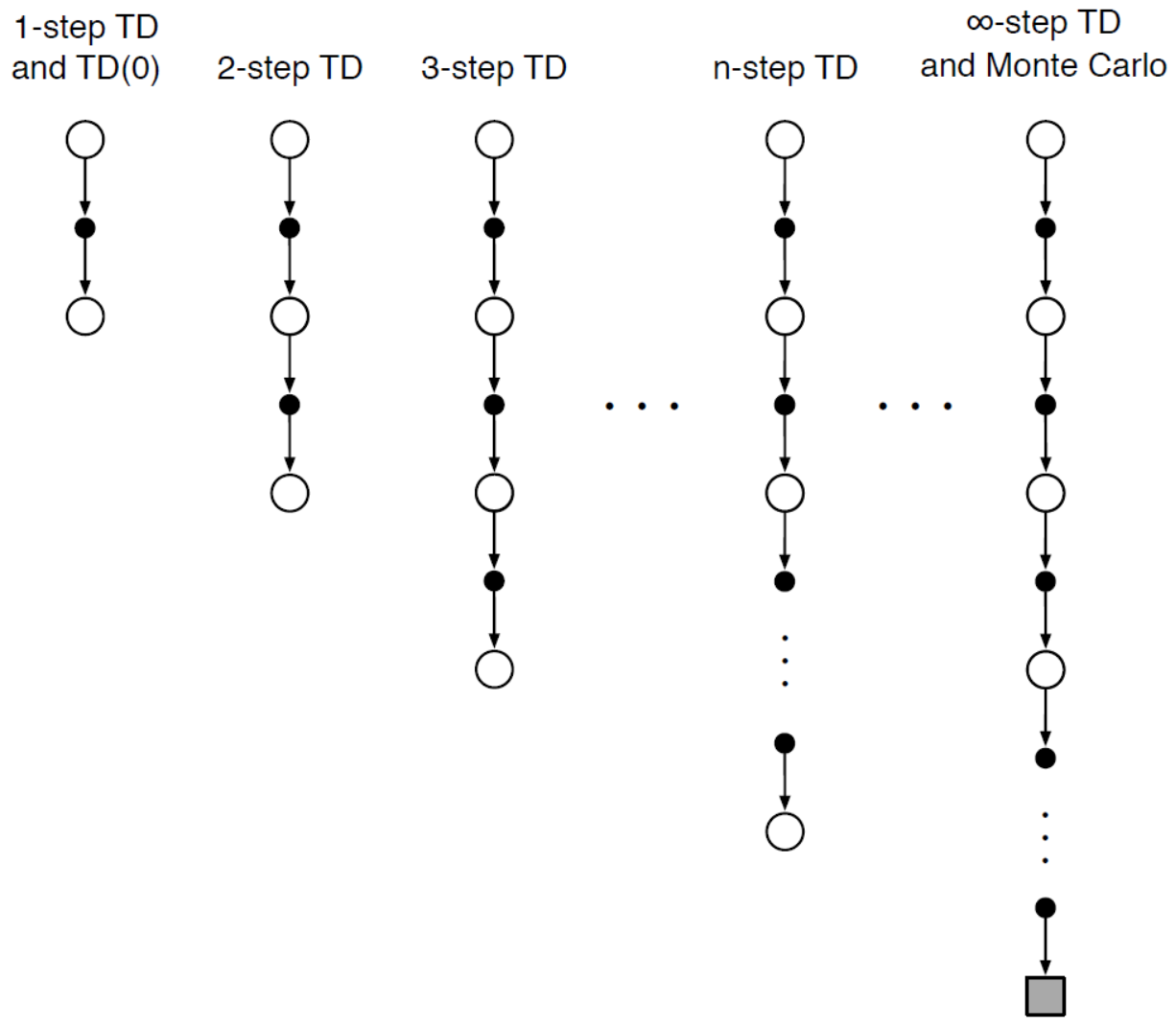
考虑采样得到一段状态-奖励序列：\(S_t,R_{t+1},S_{t+1},R_{t+2},\ldots,R_T,S_T\)。在MC方法中计算采样回报得到

\[G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots++\gamma^{T-t-1} R_T. \]

在TD(0)算法中计算采样目标价值为

\[G_{t:t+1}=R_{t+1}+\gamma V(S_{t+1}), \]

其中，\(V\)表示状态价值函数\(v_\pi\)的估计；\(G_{t:t+1}\)表示单步截断回报估计，即包含从\(t\)时刻到\(t+1\)时刻的累计奖励。同理可得，两步截断回报为

\[G_{t:t+2}=R_{t+1}+\gamma R_{t+2}+\gamma^2 V(S_{t+2}), \]

注意多步TD算法需要累计奖励，因此是延迟更新的。\(n\)步截断回报为

\[G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1}R_{t+n}+\gamma^nV(S_{t+n}), \]

那么TD(n)算法的更新公式为

\[V(S_t)=V(S_t)+\alpha[G_{t:t+n}-V(S_t)],\quad 0\leq t<T \]

TD(n)算法在开始的前\(n-1\)步并不会进行更新，因此，作为弥补会在遇到终止状态后下一轮交互开始之前，进行\(n-1\)次更新。分别根据状态-奖励序列\((S_{T-n},R_{T-n+1},S_{T-n+1},R_{T-n+2},\ldots,R_T,S_T)\)、\((S_{T-n+1},R_{T-n+2},\ldots,R_T,S_T)\)、\(\ldots\)、\((S_{T-1},R_T,S_T)\)进行更新。因为含终止状态的交互轨迹，其截断回报的采样是独立的，更值得学习。下面给出\(n\)步TD预测算法的伪代码。

TD(n)算法的一个重要性质就是\(G_{t:t+n}\)的期望与\(V(S_t)\)相比是一个对\(v_\pi\)更好的估计，即

\[\max_s|E_\pi[G_{t:t+n}|S_t=s]-v_\pi(s)|\leq\gamma^n\max_s|V(s)-v_\pi(s)|, \]

上式不等式利用了\(v_\pi\)的本质，

\[\begin{eqnarray*} v_\pi(s)&=&\mathbb{E}[G_t|S_t=s]\\ &=&\mathbb{E}[R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1}R_{t+n}+\gamma^n G_{t+n}|S_t=s]. \end{eqnarray*} \]

这个性质也被称为\(n\)步截断回报的误差减小性质（error reduction property）。根据误差减小性质，可以得到理论上的证明，TD(n)算法在适当技术条件下具有更好的收敛性质。

2. n步Sarsa

n步Sarsa是单步Sarsa的推广，其回报的计算为

\[G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1}R_{t+n}+\gamma^nQ(S_{t+n},A_{t+n}),\ n\geq1,0\leq t<T-n \]

其更新算法为

\[Q(S_t,A_t)=Q(S_t,A_t)+\alpha[G_{t:t+n}-Q(S_t,A_t)] \]

Sarsa(n)控制算法的伪代码如下图所示。

从伪代码可以看出，与TD(0)相比，其实现的复杂部分在于，需要计算\(n\)步截断回报，当遇到终止状态后，需要再进行\(n-1\)次更新。

与第六章相同，Sarsa(n)同样可以扩展为期望Sarsa算法，在自举的过程中采用状态-动作的期望代替状态-动作的采样，因此目标价值为

\[G_{t:t+n}=R_{t+1}+\cdots+\gamma^{n-1}R_{t+n}+\gamma^n\sum_a\pi(a|S_{t+n})Q(S_{t+n},a).\tag{7.1} \]

这里需要注意当状态\(s\)为终止状态，则\(Q(s,A)=0\)，期望状态价值也为0。

3. n步离线策略学习

回顾一下离线策略（off-policy）学习，学习过程中采用两种策略，一个用于交互的策略\(b\)，另一个最优策略\(\pi\) 。一般来说， \(\pi\)是确定性策略，而\(b\)则具有更强探索性的。通过交互策略去估计最优策略的状态价值，需要引入重要性采样技术，可得最优策略的状态更新为

\[V(S_t)=V(S_t)+\alpha\rho_{t:t+n-1}[G_{t:t+n}-V(S_t)],\quad 0\leq t<T,\tag{7.2} \]

其中，\(\rho_{t:t+n-1}\)是重要性采样率，即

\[\rho_{t:h}=\prod_{k=t}^{\min(h,T-1)}\frac{\pi(A_k|S_k)}{b(A_k|S_k)} \]

这里值得对式（7.1）的更新方式做出一些解释，读者可能会疑惑为什么更新式不是

\[V(S_t)=V(S_t)+\alpha[\rho_{t:t+n-1}G_{t:t+n}-V(S_t)].\tag{7.3} \]

不同于第五章的MC离线策略方法，根据交互策略\(b\)的采样回报\(G_t\)和重要性采样率\(\rho_t\)，从而获得最优策略\(\pi\)的回报\(\rho_tG_t\)。TD(n)算法采取的是自举的方式，即用估计值去更新，那么目标状态价值估计\(G_{t:t+n}\)是基于最优策略\(\pi\)的状态价值估计而计算得到的。采用式（7.3）也是可行的，因为从期望的角度看，最终会逐渐逼近目标策略的状态价值，这也要求回报\(G_{t:t+n}\)采用式（7.1）进行计算更好。从第4节开始会针对目标价值\(\rho_{t:t+n-1}G_{t:t+n}\)进行改进，引入控制变量从而提高算法的稳定性。

进一步分析式（7.2），将其改写为

\[\begin{eqnarray*} V(S_t)=(1-\alpha\rho_{t:t+n-1})V(S_t)+\alpha\rho_{t:t+n-1}G_{t:t+n} \end{eqnarray*} \]

根据第五章对重要性采样率\(\rho\)的分析，当交互策略和最优策略差异性较大时，\(\rho\)的方差会很大，因此为了保证算法收敛，学习率\(\alpha\)需要足够小。

同理，\(n\)步Sarsa的更新可以对照式（7.2）得

\[Q(S_t,A_t)=Q(S_t,A_t)+\alpha\rho_{t:t+n}[G_{t:t+n}-Q(S_t,A_t)] \]

上式需要注意，重要性采样率为\(\rho_{t:t+n}\)，因为\(t+n\)时刻也需要选取一个动作。下面给出Sarsa(n)算法的离线策略控制形式的伪代码。

Sarsa(n)算法同样也可以扩展为期望Sarsa(n)算法，但由于目标状态估计是由期望估计构成，与\(t+n\)时刻的动作无关。因此，期望Sarsa(n)算法的重要性采样率为\(\rho_{t:t+n-1}\)，两者更新式子非常接近，参考式（7.1）。这里就不再列出。

4. 带控制变量的全决策方法

正如第3节所讨论的，由于重要性采样率的高方差使得离线策略学习效率较低。这里引入递推决策的重要性采样思想，假设\(n\)步自举的范围终止于\(h\)，可得\(n\)步截断回报的递推形式为

\[G_{t:h}=R_{t+1}+\gamma G_{t+1:h},\quad t<h<T, \]

其中，\(G_{h:h}=V(S_h)\)。现考虑存在两个不同的策略，交互策略\(b\)和目标策略\(\pi\)。每一次交互所涉及的奖励\(R_{t+1}\)和下一时刻的状态\(S_{t+1}\)都需要引入重要性采样率\(\rho_t=\frac{\pi(A_t|S_t)}{b(A_t|S_t)}\)。下面给出一种更为成熟的\(n\)步截断回报为

\[G_{t:h}=\rho_t(R_{t+1}+\gamma G_{t+1:h})+(1-\rho_t)V(S_t),\quad t<h<T \]

当\(\rho_t=0\)时，目标状态价值估计将不再是0，而是维持不变。上式中第二项就被称为控制变量，当\(\rho\)较大时，控制变量可以防止\(G_{t:h}\)过大。因此，它可以有效减少方差，提升算法效率。同时，控制变量并不会影响\(G_{t:h}\)的期望，因为\(E[\rho_t]=1\)，

\[E[\rho_t]=E[\frac{\pi(a|s)}{b(a|s)}]=\sum_ab(a|s)\frac{\pi(a|s)}{b(a|s)}=1 \]

相比于前面所讨论的状态价值的估计，对于状态-动作价值函数的学习，由于第一个动作并在重要性采样率中发挥作用，因此并不需要考虑\(\rho_t\)，而引入\(\rho_{t+1}\)，可得

\[G_{t:h}=R_{t+1}+\gamma\rho_{t+1}G_{t+1:h} \]

引入控制变量可得

\[\begin{eqnarray*} G_{t:h}&=&R_{t+1}+\gamma(\rho_{t+1}G_{t+1:h}+(1-\rho_{t+1})Q(S_{t+1},A_{t+1}))\\ &=&R_{t+1}+\gamma\rho_{t+1}(G_{t+1:h}-Q(S_{t+1},A_{t+1}))+\gamma Q(S_{t+1},A_{t+1})\tag{7.4} \end{eqnarray*} \]

最后一项可以用期望值替代，即

\[\bar{V}(S_{t+1})=\sum_a b(a|s)Q(S_{t+1},a) \]

值得注意的是，本节所讨论的回报估计都是基于交互策略的。博主认为Sarsa算法作为一个在线策略学习算法有其简单高效的特点。而第3节和第4节所讨论的Sarsa算法的离线策略学习形式，更适合于预测问题（策略评价），而非决策问题。本书的作者应该是为了提供完整的研究脉络而提供这两节的研究路线。

5. 去重要性采样的离线策略学习：n步树备份算法（tree backup）

下图给出3步树备份算法的计算图。沿着中心脊柱，在图中标记有3次交互的状态和奖励，以及对应的2次动作。这些是表示由初始状态-动作对\((S_t,A_t)\)之后发生的随机变量。悬挂于两侧的状态都是未选择的动作。对于最后一种状态，所有动作都被视为尚未选择。由于无法对未选择的动作采集样本数据，因此，采用自举的方式。

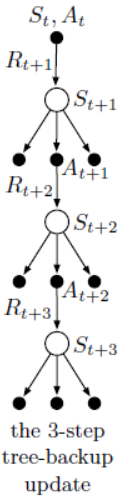
之前所涉及的算法，都是从树的顶部节点开始，不断累积交互过程中的奖励和底部节点的价值估计。但在树备份算法中，会将交互过程中未选择的动作分支也考虑在内。这也是树备份算法的核心思想。具体而言，单步树备份算法的目标价值与期望Sarsa是一致的，即

\[G_{t:t+1}=R_{t+1}+\gamma\sum_a\pi(a|S_{t+1})Q(S_{t+1},a). \]

2步树备份算法中，第一级未选择的动作价值用\(\pi(a|S_{t+1})\)加权其估计值，第二级未选择的动作用\(\pi(A_{t+1}|S_{t+1})\pi(a'|S_{t+2})\)加权其估计值，可得

\[\begin{eqnarray*} G_{t:t+2}&=&R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q(S_{t+1},a)+\gamma\pi(A_{t+1}|S_{t+1})(R_{t+2}+\gamma \bar{V}(S_{t+2}))\\ &=&R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q(S_{t+1},a)\\ & & +\gamma \pi(A_{t+1}|S_{t+1})(R_{t+2}+\gamma \sum_a\pi(a|S_{t+2})Q(S_{t+2},a))\\ &=&R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q(S_{t+1},a)+\gamma \pi(A_{t+1}|S_{t+1})G_{t+1:t+2} \end{eqnarray*} \]

n步树备份算法中，目标价值估计的递推形式为

\[G_{t:t+n} = R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q(S_{t+1},a)+\gamma \pi(A_{t+1}|S_{t+1})G_{t+1:t+n} \]

其状态-动作价值更新式为

\[Q(S_t,A_t)=Q(S_t,A_t)+\alpha[G_{t:t+n}-Q(S_t,A_t)] \]

下面给出\(n\)步树备份控制算法的伪代码。

从伪代码中可以看出，整个算法有三层嵌套循环，有其在第三层循环中需要遍历每一层所有的动作，计算量相当大。树备份算法将一段轨迹的所有动作纳入考量，是TD算法与动态规划的结合，采用期望的方式估计目标状态价值，因此不需要引入重要性采样，同时也是一种离线策略算法。

6. 联合算法：n步\(Q(\sigma)\)

到目前为止，共讨论了三种动作价值学习方法，分别是Sarsa(n)算法、期望Sarsa算法、树备份算法。Sarsa(n)算法是完全基于交互采样学习的算法，期望Sarsa算法在交互的最后节点采用期望估计，而树备份算法在所有节点都采用期望估计。将这三种方式综合起来，令\(\sigma_t\in\{0,1\}\)指示在时刻\(t\)的更新方式，其中\(\sigma_t=1\)表示用采样数据更新，\(\sigma_t=0\)表示用期望更新。其计算图如下图所示。

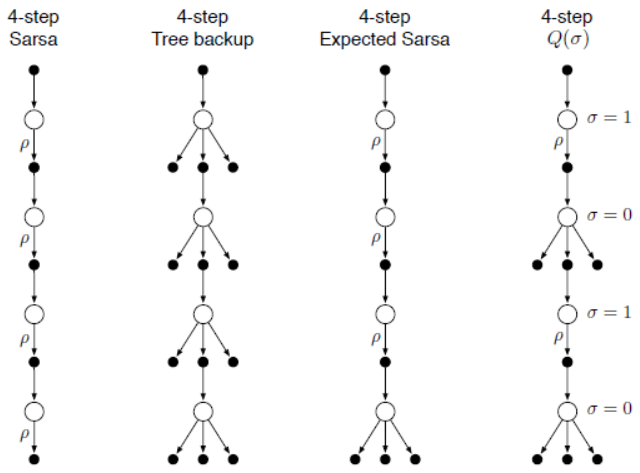
根据第4节中的式(7.4)，给出联合算法\(Q(\sigma)\)的离线策略学习的一般形式：

\[G_{t:h}=R_{t+1}+\gamma(\sigma_{t+1}\rho_{t+1}+(1-\sigma_{t+1})\pi(A_{t+1}|S_{t+1}))(G_{t+1:h}-Q(S_{t+1},A_{t+1}))+\gamma\bar{V}(S_{t+1}) \]

其具体实现的伪代码如下图所示。

7. 小结

本章主要讨论了TD学习算法族类，它是MC算法与TD(0)算法的中间产物。\(n\)步TD算法延迟了\(n\)步再进行更新，与TD(0)算法相比，它的更新更加准确。\(n\)步\(Q(\sigma)\)算法是期望Sarsa和Q-learing算法更一般化的表示形式。\(n\)步\(Q(\sigma)\)算法往往需要更多的计算量和存储空间。针对离线策略学习方式，本章给出了两种算法，一种基于重要性采样技术，另一种基于树备份（tree-backup）技术。

8.实验

Random Walk 预测问题

考虑一个马尔可夫奖励过程（Markov reward process, MRP），每轮交互都从中心状态开始，每个状态可以随机选择向左或者向右两种动作，两个动作的选择概率为50%。每轮交互的结束状态位于最左端和最右端，当智能体到达最右端获得奖励\(R=+1\)，到达最左端获得奖励\(R=-1\)，其他状态转移的奖励均为\(R=0\)。本次MRP过程共有19个状态，利用TD(n)算法估计其状态价值。

在实现过程中，其核心部分包含两点，1.实现\(n\)步累积奖励，如果最后状态不是最终状态，则还需加上最后状态的价值估计；2.遇到终止状态之后，还需要进行\(n\)次更新。其核心代码如下所示。

time += 1
update_time = time - n
if update_time >= 0:
    returns = 0.0
    # 计算累计奖励
    for t in range(update_time + 1, min(T, update_time + n) + 1):
        returns += pow(GAMMA, t - update_time - 1) * rewards[t]
    # 加上最后的状态价值估计
    if update_time + n <= T: 
        returns += pow(GAMMA, n) * value[states[(update_time + n)]]
    state_to_update = states[update_time]
    # 更新状态价值
    if not state_to_update in END_STATES:
        value[state_to_update] += alpha * (returns - value[state_to_update])
if update_time == T - 1:
    break

具体代码参照随书代码random_walk.py。总共进行10轮交互，为了保证实验结果的一般性，共进行了100轮重复实验取均值，实验结果如下图所示。

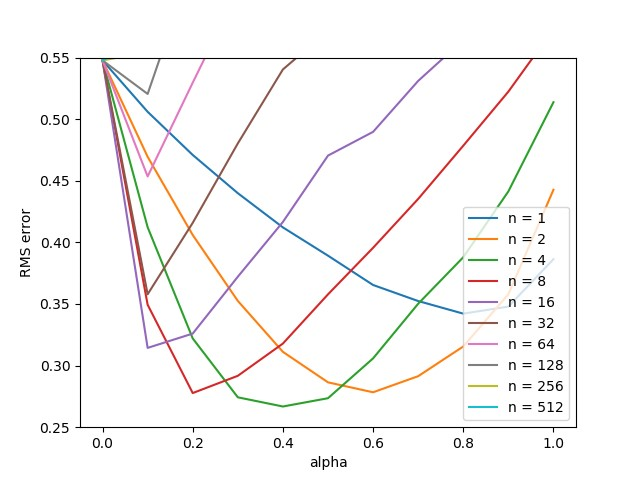
从实验结果看，TD(\(n\))算法的瞬时表现随着\(n\)的增加而提升，但是随着\(n\)的增加，相应要求学习率要足够的小，否则会出现较大抖动。