强化学习读书笔记--第四章动态规划

动态规划（dynamic programming, DP）是建立在完美的MDP模型上的算法，即能够准确知道所有状态转移概率\(p(s',r|s,a)\)。动态规划的思想对于后面理解强化学习方法是非常重要的。一般来说，考虑将环境构建为有限MDP，对于连续的任务，也可以将其离散后当作有限MDP。DP的核心思想就是通过构造状态价值函数来搜索最优策略。如第三章所述，可以通过求解贝尔曼最优公式得到最优策略，即

\[\begin{eqnarray*} v_*(s)&=&\max_a\mathbb{E}\left[R_{t+1}+\gamma v_*(S_{t+1})|S_t=s,A_t=a\right]\\ &=&\max_a\sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')] \end{eqnarray*} \]

或是Q函数的贝尔曼最优公式：

\[\begin{eqnarray*} q_*(s,a)&=&\mathbb{E}\left[R_{t+1}+\gamma\max_{a'}q_*(S_{t+1},a')|S_t=s,A_t=a\right]\\ &=&\sum_{s',r}p(s',r|s,a)[r+\gamma\max_{a'}q_*(s',a')] \end{eqnarray*} \]

DP算法就是基于贝尔曼最优公式去近似得到最优价值函数。

1.策略评估（policy evalution/prediction）

首先考虑如何根据任意策略计算其对应的状态价值函数，也称为策略评估，这类问题称为预测问题。重写第三章的状态价值函数计算方法：

\[\begin{eqnarray*} v_\pi(s)&=&\mathbb{E}[G_t|S_t=s]\\ &=&\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+v_\pi(s')] \end{eqnarray*} \]

假设环境的动态是已知的，那么通过贝尔曼公式来更新价值函数，与第三章的实验方式是相同的。

\[v_\pi^{(k+1)}(s)=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+v_\pi^{(k)}(s')] \]

随着迭代次数\(k\)趋向于无穷大，状态价值函数\(v_\pi^{(k)}\)趋向于策略\(\pi\)下的状态价值的真实值，这个算法被称为迭代策略评估（iteration policy evaluation）。这种迭代更新方式也称为期望更新（expected update），因为它是基于所有可能的下个状态而不是通过采样获得的。

​ 根据期望更新，可以建立两个数组，一个储存旧值，一个储存新值，这样新值可以依序通过旧值计算，即同步更新方式。也可以只建立一个数组，通过原位（in place）更新的方式来完成，即异步更新方式。异步方式算法收敛会更快。通常将所有状态更新过一轮，称为一个扫描（sweep）。下图为给定策略\(\pi\)的异步更新方式实现的策略估计（伪代码）。

2. 策略改进（policy improvement）

计算状态价值函数的原因是为了帮助我们寻找更好的策略。当计算出状态\(s\)价值\(v_\pi(s)\)后，如果需要知道当策略改变时，即\(a\neq\pi(s)\)，那么状态价值\(v(s)\)会变得更好还是更坏。考虑状态-动作价值函数：

\[q_\pi(s,a):=\mathbb{E}\left[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s,A_t=a\right]\\ =\sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi(s')] \]

假设一个新的策略\(\pi'\)相比于旧策略\(\pi\)，只是在状态\(s\)上选择了新的动作\(a\)，接下来的所有状态仍采用旧策略\(\pi\)。那么判断新策略\(\pi'\)是否比旧策略\(\pi\)好的关键在于，判断新动作\(a\)是否比动作\(\pi(s)\)好，即\(q_\pi(s,\pi'(s))\)的值是否大于\(v_\pi(s)\)值，这被称为策略改进理论（policy improvement theorem）：

\[q_\pi(s,\pi'(s))\geq v_\pi(s) \]

如果满足上式，那么策略\(\pi'\) 则好于\(\pi\)。由此，可得其期望价值满足

\[v_{\pi'}(s)\geq v_{\pi(s)}. \]

由此可以得出策略改进的方法：

\[\pi'(s):=\arg \max_a q_\pi(s,a) \]

策略改进的方式等价于求解贝尔曼最优公式\(v_*(s)\)。

3. 策略迭代（policy iteration）

给定一个策略，通过策略评估得到其状态价值函数，然后改进策略，再进行策略评估，如此循环往复可以得到一个序列：

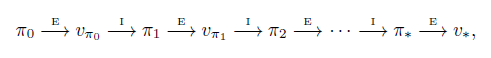
上述过程称为策略迭代（policy iteration）。下图给出了策略迭代算法的伪代码。

4. 价值迭代（value iteration）

策略迭代的明显缺点是每次改进策略后都需要进行策略估计，这样非常消耗时间和空间。但是采用价值迭代就没有这个问题，它将策略改进与策略评估相结合，在对某个状态进行策略评估的同时选择最优动作：

\[\begin{eqnarray*} v_{k+1}(s)&:=&\max_a\mathbb{E}\left[R_{t+1}+\gamma v_k(S_{t+1})|s_t=s,A_t=a\right]\\ &=&\max_a\sum_{s',r}p(s',r|s,a)[r+v_k(s')] \end{eqnarray*} \]

对比策略评估方法，价值迭代是将状态-动作的最大值纳入考量，而非所有动作所构成的期望价值。在评估策略的同时选择最优策略。其算法如下图所示：

5. 异步动态规划

动态规划的主要的缺点在于需要不断的扫描整个状态空间，当状态数量很多时，计算会消耗大量的时间。异步DP算法使用任意的顺序来更新可获得的状态，因此有些状态的值会在更新其他状态前被更新多次。为了保证所有状态都被计算，每隔一定时间后，所有状态都会被强制更新一次。

6. 广义策略迭代（generalized policy iteration）

使用广义策略迭代（GPI）来指代一般意义上的策略估计与策略改进相互作用的过程。几乎所有的强化学习方法都属于广义策略迭代。如下图所示。

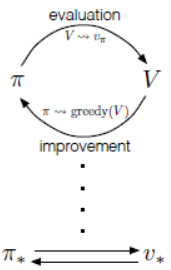
GPI的评估和改进过程既可以看作是竞争过程，也可以看作是合作过程。从某种意义上说，他们竞争的方向是相反的。根据状态价值函数通过贪婪动作改进策略的同时，使得状态价值函数不再正确。若状态价值函数与策略一致通常会使该策略不再是贪婪动作。然而，从长远来看，这两个过程相互作用，最终找到一个单一的联合解决方案，即最优价值函数和最优策略。过程如下图所示。

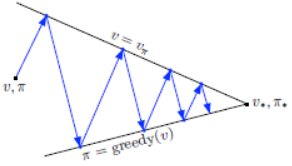
7. 动态规划的效率

DP不擅长解决大状态空间的问题，但是相比其他的算法，DP的计算效率还是比较高的。DP的时间复杂度是动作与状态数量的多项式函数。线性规划也可以快速解决MDP，但仅限于小的状态空间。DP被限制应用的重要原因是维数灾难（curse of dimensionality），当状态空间的变量增加时，状态数量会成指数级增长。

当然，DP并非不能用于解决复杂问题。异步DP算法往往可以用于复杂问题，对于某些问题，虽然存在维数灾难，但该问题仍然有可能解决，因为沿着最优解轨迹出现的状态相对较少。

8. 小结

本章学习了动态规划，主要涉及策略评估、策略改进、策略迭代和价值迭代。GPI是强化学习中一个重要的概念，基本上所有强化学习算法都会涉及。异步DP算法可以更有效率地进行计算。最后，类似于DP这样利用估计值更新估计值的方式称为自举（bootstrapping），这也是强化学习中一个重要的概念。

9.实验

实验1：汽车租赁调度问题

​ Jack为一家全国性的汽车租赁公司管理着两个地点。每天都有一定数量的客户到达这两个地点租车。如果Jack有车，就会把车租出去，并收费10美元。如果在那个地方没有车，那么生意就没了。汽车归还后第二天即可出租。为了确保汽车使用率，Jack可以将两地的车相互转移，每辆车的转移费用为2美元。假设每个地点租赁和归还的汽车数量服从泊松分布，这意味着数量为n的概率为\(\frac{\lambda^n}{n!}e^{-\lambda}\)，其中\(\lambda\)是预期数量。假设\(\lambda\)对于第一和第二地点的租赁需求分别为3和4，归还需求分别为3和2。

​ 为了简化问题，假设每个地点的汽车数量不超过20辆（任何额外的汽车都会退还给公司），并且一个晚上最多可以将五辆汽车从一个地点转移到另一个地点。折扣取为\(\gamma=0.9\)，并将问题考虑为一个连续的有限MDP，时间步长为天，状态为一天结束时每个地点的汽车数量，动作为夜间在从地点一向地点二移动的汽车数量。请根据该问题找到每个状态的最优策略。

解决过程：

无论是采用策略迭代算法还是采用价值迭代算法，其核心都在于计算

\[q(s,a)=\sum_{s',r}p(s',r|s,a)[r+\gamma \cdot v(s')] \]

这要求必须要知道环境的动态信息，即状态转移的概率\(p(s',r|s,a)\)。在汽车租赁调度问题中，汽车租赁需求是随机的，使得奖励\(r\)也是随机的。奖励\(r\)由两部分构成，一个是车辆转移费用，即\(-2*|a|\)，另一个是车辆租赁的实际收入，它受当地实际汽车数量制约。下个状态\(s'\)也是随机的，它由汽车存量、汽车租赁需求和汽车归还需求所共同决定，因此要遍历所有可能的状态是一个四层的循环（租赁两层，归还两层）。

值得注意的是，\(\max_a q_\pi(s,a)=v_\pi(s)\)。

程序实现

具体代码参照随书代码car_rental.py。采用策略迭代算法，其核心代码在于三点。

• 期望回报\(q(s,a)\)的计算，即函数expected_return

  for rental_request_first_loc in range(POISSON_UPPER_BOUND+1):
      for rental_request_second_loc in range(POISSON_UPPER_BOUND+1):
          # probability for current combination of rental requests
          prob = poisson_probability(rental_request_first_loc, RENTAL_REQUEST_FIRST_LOC) * poisson_probability(rental_request_second_loc, RENTAL_REQUEST_SECOND_LOC)
  
          .....#省略的代码是计算实际租赁的车辆数量
              # get credits for renting
          reward = (valid_rental_first_loc + valid_rental_second_loc) * RENTAL_CREDIT
             
          for returned_cars_first_loc in range(POISSON_UPPER_BOUND):
              for returned_cars_second_loc in range(POISSON_UPPER_BOUND):
                  prob_return = poisson_probability(returned_cars_first_loc, RETURNS_FIRST_LOC) * poisson_probability(returned_cars_second_loc, RETURNS_SECOND_LOC)
                  ......#省略的代码是根据实际归还的车辆数量，得到下一个状态
                  prob_ = prob_return * prob
                  #计算回报期望
                  returns += prob_ * (reward + DISCOUNT * state_value[num_of_cars_first_loc_, num_of_cars_second_loc_])
  return returns
  

• 策略评估的实现

  遍历所有状态，在给定策略的情况下迭代计算状态价值，直至收敛。

  while True:
      old_value = value.copy()
      # 遍历所有的状态，采用异步方式更新状态价值
      for i in range(MAX_CARS + 1):
          for j in range(MAX_CARS + 1):
              new_state_value = expected_return([i, j], policy[i, j], value, constant_returned_cars)
              value[i, j] = new_state_value
      max_value_change = abs(old_value - value).max()
      if max_value_change < 1e-4:
          break
  

• 策略改进的实现

  根据给定的状态价值函数，遍历所有动作，选择贪婪动作。

  policy_stable = True
  for i in range(MAX_CARS + 1):
      for j in range(MAX_CARS + 1):
          old_action = policy[i, j]
          action_returns = []
          for action in actions:
              if (0 <= action <= i) or (-j <= action <= 0):
                  action_returns.append(expected_return([i, j], action, value, constant_returned_cars))
              else:
                  action_returns.append(-np.inf)
          new_action = actions[np.argmax(action_returns)]
          policy[i, j] = new_action
          if policy_stable and old_action != new_action:
              policy_stable = False
  

实验结果：

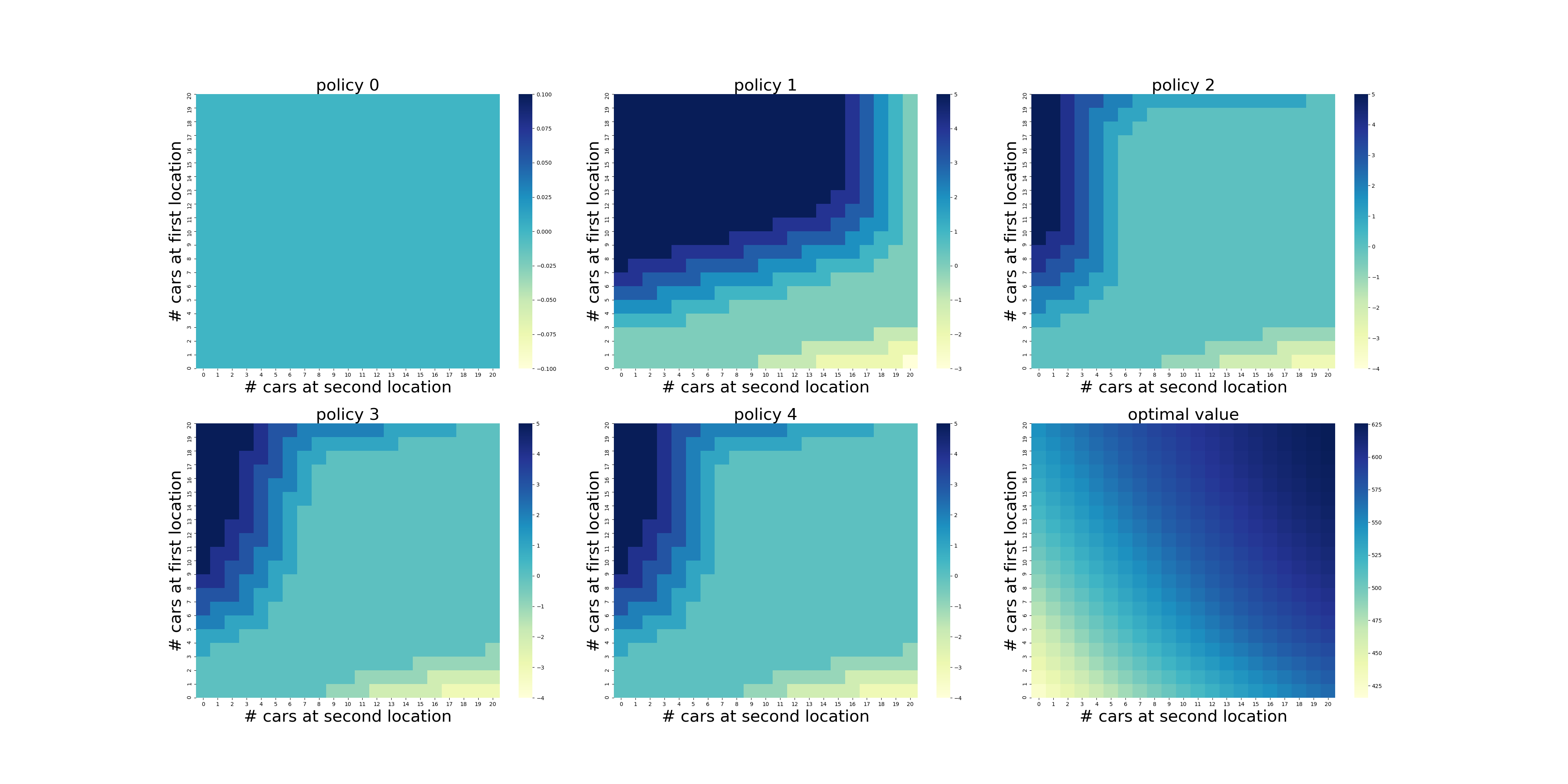
实验结果符合正常认知，两地车辆存有量越多，状态价值越高。地点一租赁需求为3，归还需求为3，供需平衡，因此，从异地运送车辆的需求也小。地点二租赁需求为4，归还需求为2，因此需要地点一送车过来。

实验2：赌徒问题

​ 赌徒有机会在一系列掷硬币的结果上下注。如果硬币正面朝上，他赢得的与他下注的金钱一样多；如果是反面，他就失去了赌注。当赌徒达到100元的目标则获胜，若因钱用完而失败，则游戏结束。在每一次下注中，赌徒必须将其资本的一部分以整数为单位进行游戏。状态是赌徒的资本\(s\in\{1,2,\cdots,100\}\)，动作是赌注\(a\in\{1,\cdots,\min(s,100−s)\}\)。奖励为零，除非赌徒达到目标则奖励为\(+1\)。当资本为0时，则表示赌徒输了，奖励为-1。

​ 状态价值函数给出从每个状态出发获胜的概率。策略是从资本到赌注的映射。最优策略使达到目标的概率最大化。\(p_h\)表示硬币正面朝上的概率。如果\(p_h\)已知，那么环境的动态就是已知的。

解决过程：

​ 相比于实验1，赌徒问题的环境动态较为简单，状态转移过程只有两种，一个是以\(p_h\)的概率从状态\(s\)转移到状态\(s+a\)，另一个是以\(1-p_h\)的概率从状态\(s\)转移到状态\(s-a\)​。其核心都在于计算

\[\begin{eqnarray*} q(s,a)&=&p_h*[r+\gamma \cdot v(s+a)]+(1-p_h)*[r+\gamma \cdot v(s-a)]\\ v(s)&=&\max_a q(s,a) \end{eqnarray*} \]

这里采用价值迭代的方式，获得最有价值函数，然后得到最优策略。

程序实现

具体代码参照随书代码gamblers_problem.py。其核心代码在于价值迭代和最优策略计算。

• 价值迭代

  for state in STATES[1:GOAL]:
      # get possilbe actions for current state
      actions = np.arange(1,min(state, GOAL - state) + 1)
      action_returns = []
      for action in actions:
          action_returns.append(HEAD_PROB * state_value[state + action] + (1 - HEAD_PROB) * state_value[state - action])
      new_value = np.max(action_returns)
      state_value[state] = new_value
      delta = abs(state_value - old_state_value).max()
      if delta < 1e-9:
          break
  

• 最优策略计算

  policy = np.zeros(GOAL + 1)
  for state in STATES[1:GOAL]:
      actions = np.arange(min(state, GOAL - state) + 1)
      action_returns = []
      for action in actions:
          action_returns.append(HEAD_PROB * state_value[state + action] + (1 - HEAD_PROB) * state_value[state - action])
  
      policy[state] = actions[np.argmax(np.round(action_returns[1:], 5)) + 1]
  

当然在价值迭代的过程中，可以同步更新最优策略，当状态价值函数收敛后，最优策略也能获得了。

实验结果：

当\(p_h\)取不同值时，得到的状态价值函数曲线是不同的。

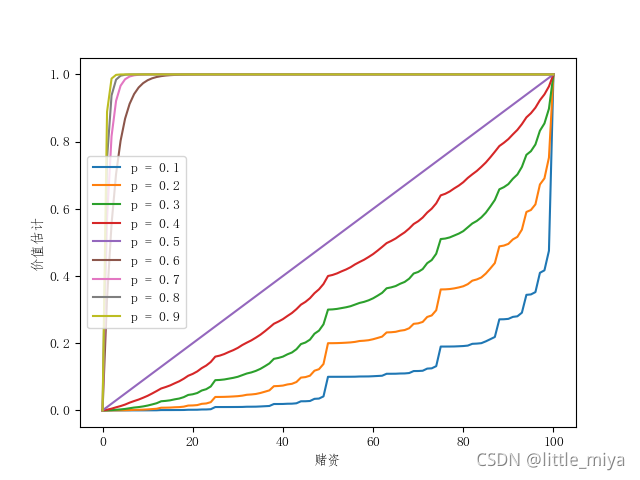
可以看出，当每次游戏赢的概率\(p_h>0.5\)时，概率越大，其状态价值函数的上升曲线越陡峭。这符合正常的认知，\(p_h\)概率越大，赌资哪怕很小赢的概率也是很大的。反之，如果\(p_h\)概率越小，赌资哪怕很大赢的概率也会很小。所以其状态价值函数曲线会比较平缓。

最优策略就两种，当\(p_h\geq0.5\)时，其最优策略为

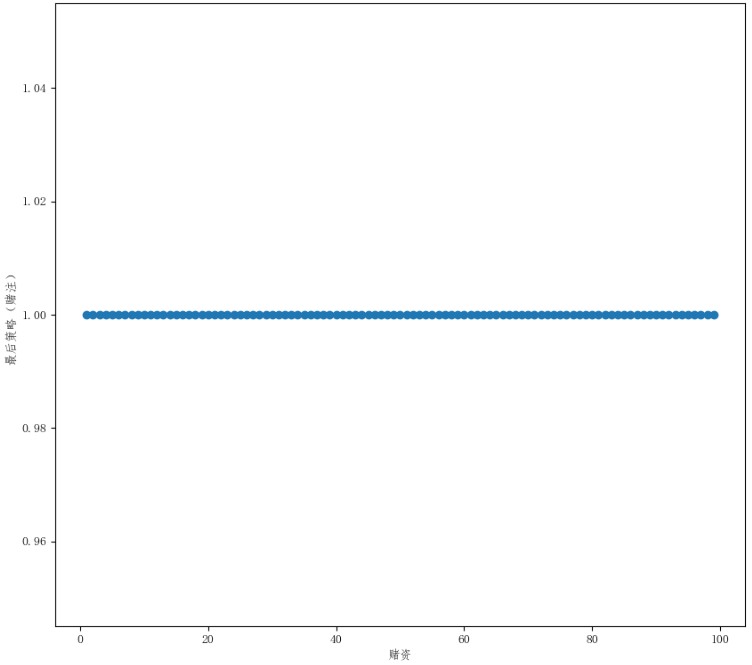
当\(p_h<0.5\)时，最优策略为

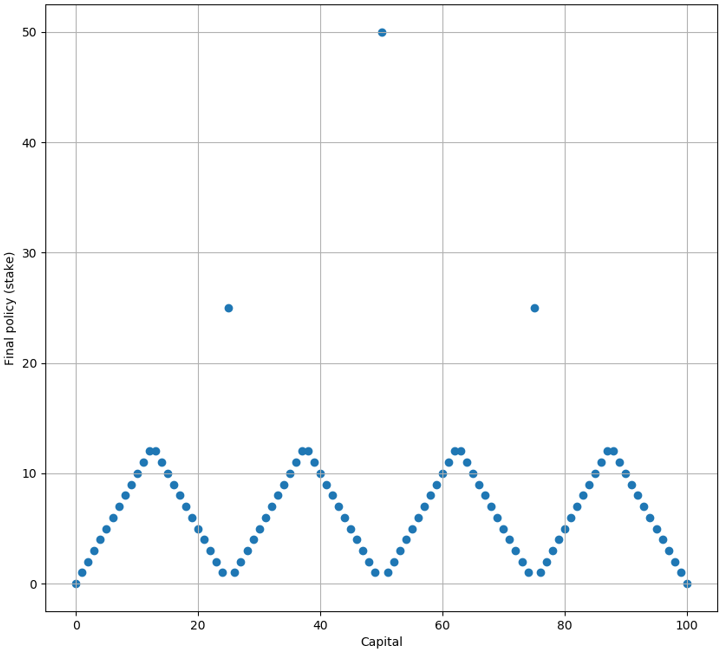
这样的策略一开始计算得到的时候时让人感到惊讶的，但是仔细一想却是合乎逻辑的。当\(p_h>0.5\)时，这意味着游戏的局数越多，则赢的局数越多。因此其最优策略是尽可能进行更多的游戏次数，所以每次的赌注只采用\(a=1\)。同理，当\(p_h<0.5\)时，这意味着游戏的局数越多，则输的局数越多。因此其最优策略时尽可能在最少的游戏次数下，达到游戏目标。因此在赌资分别为\(s=25,50,75\)时，会采用\(a=25,50,25\)。当赌资\(s<25\)时，尽可能达到\(s=25\)。当赌资\(25<s<50\)时，尽可能达到\(s=50\)。当赌资\(50<s<75\)时，尽可能达到\(s=75\)。如此这样，游戏的局数是最少的。