强化学习读书笔记 -- 第三章有限马尔可夫决策过程

本章将利用有限马尔可夫决策过程（Finite Markov Decision Process，finite MDP）描述智能体与环境进行交互的过程。MDP是经典的序列决策过程，每一次决策的动作所产生的影响不仅包括了瞬时奖励（即采取的行为立刻带来的奖励），还包括由此带来的后续影响（涉及未来的奖励，类似蝴蝶效应）。因此，MDPs需要考虑瞬时奖励与延迟奖励的平衡问题。与多臂Bandits问题不同，多臂Bandits问题里估计的是动作价值函数\(q_*(A)\)（因为其环境是静态的），MDPs问题中估计的是动作价值函数\(q_*(S,A)\)，或状态价值函数\(v_*(S)\)。MDPs是强化学习的理想化数学形式，在人工智能领域中，实用性与数学理论的可描述性始终都存在矛盾的。

1.智能体-环境交互

智能体与环境的交互过程如图3.1所示。

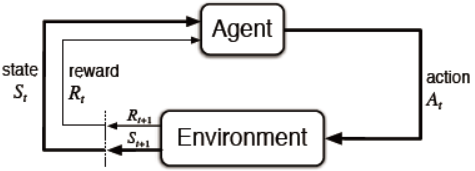
​图3.1 MDPs中智能体与环境交互过程

在交互的过程中，离散化时间序列会形成一个序列或轨迹（trajectory）：

\[S_0,A_0,R_1,S_1,A_1,R_2,S_2,R_3,\cdots \]

这里需要注意，奖励\(R_1\)是基于状态\(S_0\)和动作\(A_0\)得到的。在有的文献中会写成\(R_0\)。

在有限MDP中，状态、动作与奖励的集合都是有限的。这种情况下，变量\(R_t\)与\(S_t\)可以描述成离散概率分布形式，且仅取决于前一时刻的状态\(S_{t-1}\)与动作\(A_{t-1}\)，即

\[p(s',r|s,a) := \text{Pr}\{S_t=s',R_t=r|S_{t-1}=s,A_{t-1}=a\} \]

\(p(s',r|s,a)\)就是对环境动态的描述，且满足马尔可夫性质。对给定的\((s,a)\)，其所有可能的概率转移之和为1：

\[\sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}}p(s',r|s,a)=1, \text{for all}\ s\in\mathcal{S},a\in\mathcal{A(s)} \]

通过\(p(s',r|s,a)\)，可以得到与环境状态相关的所有信息，例如状态转移概率（state-transition probabilities），

\[p(s'|s,a)=\sum_{r\in\mathcal{R}}p(s',r|s,a) \]

状态-动作\((s,a)\)组下的期望奖励，

\[r(s,a)=\mathbb{E}[R_t|S_{t-1}=s,A_{t-1}=a]=\sum_{r\in\mathcal{R}}r\sum_{s'\in\mathcal{S}}p(s',r|s,a) \]

状态-动作-转移状态\((s,a,s')\)组下的期望奖励，

\[r(s,a)=\mathbb{E}[R_t|S_{t-1}=s,A_{t-1}=a,S_t=s']=\sum_{r\in\mathcal{R}}r\frac{p(s',r|s,a)}{p(s'|s,a)} \]

注：此处利用贝叶斯推导式\(p(s',r|s,a)=p(r|s,a,s')p(s'|s,a)\)。

​MDP框架相对来说比较抽象与灵活，可以应用于不同的场景。MDP框架并不要求采样时间是固定的。动作既可以是低阶的控制，如电机转速，也可以是高阶的决策等。同样，状态既可以是环境测量数据也可以是抽象后的高阶特征等。需要注意的是智能体与环境的边界不同于现实世界的认知，如机器人与所处环境，通常将机器人执行结构的传感数据同样认为是环境。奖励虽然是在智能体内部进行计算的，但是被认为是智能体外在的激励。下面举几个例子来帮助理解，智能体、环境和奖励的区分。

• 生物反应器

  假设应用强化学习来训练生物反应器（用于生产有用化学物质的大量营养物质和细菌）的温度控制和搅拌速率。动作是根据所处环境将目标温度和目标搅拌速率传递到下位的控制器，用由控制器激活加热元件和马达以实现目标。环境状态可能是热电偶和其他传感器读数，也可能是经过滤波和延迟的信号输入和代表成分和目标化学品的符号输入。奖励可能是生物反应器产生有用化学物质的速率的即时测量。注意，这里的每个状态都是传感器读数和符号输入的列表或矢量，每个动作都是由目标温度和搅拌速率组成的矢量。强化学习任务的典型特征是具有这种结构化表征的状态和动作。另一方面，奖励总是标量。

• 拾取和放置机器人

  考虑在重复的拾取和放置任务中使用强化学习来训练机械臂的运动。要想学习快速平稳的运动，智能体必须学习直接控制电机，并且可以获取相应具有低延迟的信息如连杆的当前位置和速度。这种情况下，动作可能是在每个关节处给每个电机施加的电压，状态可能是关节角度和速度的实时读数。对于成功拾取和放置的每个物体，奖励可能为+1。为了鼓励流畅的动作，在每个时间步长上，可以根据动作的瞬间“急动”给予一个小的负奖励。

2. 目标和奖励

​期望智能体实现的目标是通过特定的信号来实现的，这便被称为奖励。智能体的目标是通过最大化一个累积奖励来达成。通过奖励信号去实现目标，这是强化学习区别与其他学习的一个最明显的特征。在强化学习中，奖励的设置是比较复杂和困难的，奖励信号设置的目的在于你希望智能体实现什么样的目标，而非你希望智能体如何实现目标。另外奖励信号并不能提供智能体先验知识，先验知识可以通过初始化策略或者价值函数来实现。

3. 回报和经历（returns and episodes）

一般来说，目标是最大化的是期望回报值（expected return）。\(t\)时刻的回报就是对未来奖励的累加，

\[G_t:=R_{t+1}+R_{t+2}+\cdots+R_T, \]

其中\(T\)表示终止时间。每段经历都在一类特殊的状态停止，称为终止状态（terminal state），比如下棋胜利或者失败。这类任务被称为分段性任务（episodic tasks）。相对的，无终点的任务就被称为连续性任务（countinuing tasks）。对于无终止的任务，最大化回报会导致无穷，因此需要引入新的概念。

​下面引入的概念是折扣（discounting），不同时期的奖励值对智能体来说重要性是不同，既需要考虑短期的奖励，又需要考虑长期的奖励。因此，处于权衡的目的，智能体会最大化累积折扣奖励，或期望折扣回报（expected discounted return）：

\[G_t:=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots=\sum_{k=0}\gamma^kR_{t+k+1}, 0\leq\gamma\leq1 \]

如果\(\gamma=0\)，那么这个智能体只关注当前奖励（myopic），随着\(\gamma\)趋向于1，那么这个智能体就越注重长远奖励（farsighted）。可以给出回报的递推形式，

\[\begin{eqnarray*} G_t&=&R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots\\ &=&R_{t+1}+\gamma(R_{t+2}+\gamma R_{t+3}+\gamma^2 R_{t+4}+\cdots)\\ &=&R_{t+1}+\gamma G_{t+1} \end{eqnarray*} \]

对于终止状态下的回报，通常记为\(G_T=0\)。可以看出，给出奖励为\(R_t=1\)，当\(\gamma<1\)时，即使是连续性任务，回报也是有界的。

4. 策略和价值函数

几乎所有的强化学习都涉及到对价值函数的估计，价值函数用于衡量智能体在给定状态或动作下的好坏。根据价值函数而采取的动作模式就称为策略（policies）。正式地说，策略就是状态与每个动作的被选概率的一种映射关系。

在给定策略\(\pi\)下状态\(s\)的价值函数记为\(v_\pi(s)\)，它是在状态\(s\)之后根据策略\(\pi\)的期望回报：

\[v_\pi(s):=\mathbb{E}[G_t|S_t=s]=\mathbb{E}\left[\sum_{k=0}\gamma^kR_{t+k+1}|S_t=s\right], \]

称这样的价值函数为策略\(\pi\)的状态价值函数。

同理，定义在给定策略\(\pi\)和状态\(s\)下执行动作\(a\)的价值函数记为\(q_\pi(s,a)\)：

\[q_\pi(s,a):=\mathbb{E}[G_t|S_t=s,A_t=a], \]

称这样的价值函数为策略\(\pi\)的动作-状态价值函数，也称为Q-function。Q函数相比于状态价值函数，可以仅根据当前状态选择最优动作。

递归是状态价值函数的基本性质

\[\begin{eqnarray*} v_\pi(s)&=&\mathbb{E}[G_t|S_t=s]\\ &=&\mathbb{E}[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ &=&\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\left[r+\gamma\mathbb{E}[G_{t+1}|S_{t+1}=s']\right]\\ &=&\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\left[r+\gamma v_\pi(s')\right] \end{eqnarray*} \]

上式也称为状态价值函数的贝尔曼公式（Bellman Equation），它说明了当前状态的价值期望等于下一个状态的价值期望加上奖励期望。值得注意的是，贝尔曼公式下的状态价值函数的解是唯一的。

例子：网格世界

​图3.2（左）显示了一个简单有限MDP的矩形网格世界表示。网格的单元对应于环境的状态。在每个单元格中，有四个可选动作：北、南、东和西，不同选择使得智能体沿着相应方向在网格上移动一个单元格。向边界移动。智能体保持其位置不变，但也会得到−1的奖励。除了那些将智能体移出特殊状态A和B的动作外，其他动作的奖励为0。从状态A开始，所有四个动作的奖励都为+10，并将代理带到A'。从状态B开始，所有动作产生+5的奖励，并将智能体带到B'。

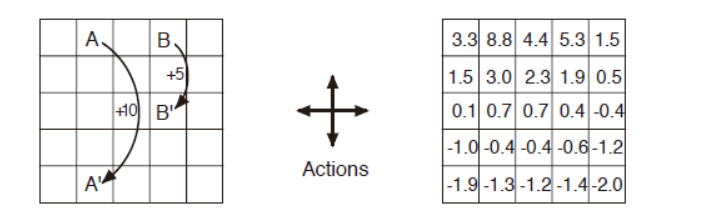
​ 图3.2 网格世界：左图为奖励方式，右图为等概率随机策略下的状态价值

​ 这里折扣系数\(\gamma=0.9\)，智能体选择每个动作的概率是一样的。可以验证右图状态价值的正确性，如\(v_\pi(A) = r+\gamma v_\pi(A')=10+0.9*(-1.3)=8.83\)。值得注意的是，从状态A出发，虽然可以得到\(r=10\)的奖励，但是它本身的价值却是小于10的。原因在于，它会到达边界状态A'（有一定概率会撞墙，从而得到惩罚\(r=-1\)）。而相比之下状态B的价值就高于其奖励。

5. 最优策略和最优值函数

定义如果一个策略\(\pi\)的价值函数对所有状态都大于等于策略\(\pi'\)，那么策略\(\pi\)就优于策略\(\pi'\)。至少有一个策略等于或好于其他所有策略，这就是最优策略，记为\(\pi_*\)。可能有多个的最优策略，他们共享一个状态值函数，称为最优状态价值函数：

\[v_*(s):=\max_\pi v_\pi(s), \text{for all}\ s\in \mathcal{S} \]

同理可以得到最优动作价值函数：

\[q_*(s,a):=\max_\pi q_\pi(s,a) \]

它们两者之间的关系为

\[q_*(s,a)=\mathbb{E}\left[R_{t+1} + \gamma v_*(S_{t+1})|S_t=s,A_t=a\right] \]

将最优价值函数改写成贝尔曼公式的形式就得到了贝尔曼最优公式（Bellman Optimality Equation），即在每次状态下选择使价值函数最大的动作来执行：

\[\begin{eqnarray*} v_*(s) &=& \max_{a\in A(s)}q_{\pi_*}(s,a)\\ &=&\max_a\mathbb{E}\left[R_{t+1} + \gamma v_*(S_{t+1})|S_t=s,A_t=a\right]\\ &=&\max_a\sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')]\\ q_*(s,a)&=&\mathbb{E}\left[R_{t+1} + \gamma q_*(S_{t+1},a')|S_t=s,A_t=a\right]\\ &=&\sum_{s',r}p(s',r|s,a)[r+\max_{a'}q_*(s',a')] \end{eqnarray*} \]

值得注意的是，状态价值函数的最优公式是在状态\(s\)下选择期望价值最大的动作，而动作-状态最优公式则是在确定当前状态\(s\)的奖励值\(r\)后，在下一个状态\(s'\)中寻找最大动作价值。

对有限MDP，贝尔曼最优公式只有唯一的最优状态价值函数。对最优状态函数采用贪婪策略即为最优策略。

例子：网格世界

​ 继续回到网格世界的例子，针对网格任务求解\(v_*\)的Bellman方程，如图3.3（左）所示。如前面所述，状态A之后是+10的奖励并过渡到状态A'，而状态B是+5的奖励并转换到状态B'。图3.3（中）显示了最优价值函数，图3.3（右）显示了相应的最优策略。如果单元格中有多个箭头，则所有相应的操作都是最优的。

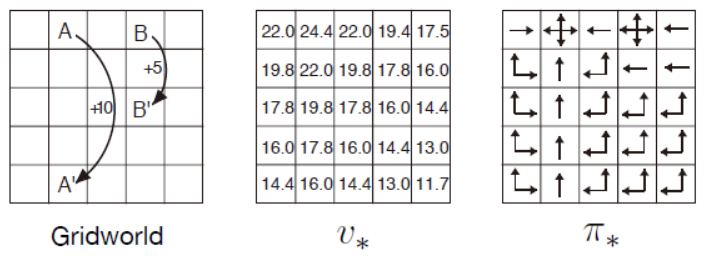
​ 图3.3 网格世界的最优策略

由此可以看出，最优价值函数是唯一的，但是最优策略却可以有很多个。

6. 最优性和近似

一般来说，我们很难获取到完整准确的环境动态信息，即使可以获取也很难通过求解贝尔曼公式获取最优策略。因为大部分的实际问题其状态空间太过庞大，由于算力和存储能力的限制，使得我们只能采用近似的方法进行求解。强化学习方法提供了一些独特的近似方式。例如，在近似最优动作时，智能体可能会面对许多低概率的状态，即使选择次优动作对累积奖励几乎没有影响。事实上，智能体可能在游戏状态集的很大一部分会做出糟糕的决定，但强化学习使得智能体对于经常遇到的状态做出良好的决策，从而接近最佳策略。这是将强化学习与其他近似求解MDP的方法区分开来的一个关键特性。

7. 小结

本章我们了解了智能体、奖励、动作、环境的关系，同时定义了策略。策略是一个令智能体根据状态选择动作的规则。我们了解了MDP的重要成分，如回报、折扣、分段性任务、连续性任务等等。学习了价值函数与贝尔曼公式、贝尔曼最优公式。值得注意的是，在实际应用中，无法完全了解所处环境，因此无法建立一个完美契合的模型。考虑近似方法来求解最优策略往往是必须要解决的问题。

8.实验 网格世界

这里再次以网格世界为例，求解网格世界的最优状态价值函数，从而得到最优策略。这里选择折扣系数为\(\gamma=0.9\)，规则与前面例子一样，采用等概率随机动作。

求解方式1：采用线性方程组求解

用矩阵\(M\)表示网格世界的状态价值函数，\(M[i,j]\)表示第\(i\)行第\(j\)列的状态价值（\(0\leq i<5, 0\leq j<5\)），由此可得每个状态价值的等式为

\[\begin{eqnarray*} 0.25*(r_上+\gamma*M[i-1,j])+0.25*(r_左+\gamma*M[i,j-1])&&\\ +0.25*(r_下+\gamma*M[i+1,j])+0.25*(r_右+\gamma*M[i,j+1])&=&M[i,j]\\ -M[i,j]+0.25\gamma*M[i-1,j]+0.25\gamma*M[i,j-1]&&\\ +0.25\gamma*M[i+1,j]+0.25\gamma*M[i,j+1]&=&-0.25(r_上+r_左+r_下+r_右) \end{eqnarray*} \]

由此，将所有状态写成扩展矩阵\(Ax=b\)的形式，其中\(x\in\R^{25}\)就是由所有状态所构成的状态向量。

程序实现

具体代码参照随书代码gird_world.py。其核心实现为

A = -1 * np.eye(WORLD_SIZE * WORLD_SIZE)
   b = np.zeros(WORLD_SIZE * WORLD_SIZE)
   for i in range(WORLD_SIZE):
       for j in range(WORLD_SIZE):
           s = [i, j]  # current state
           index_s = np.ravel_multi_index(s, (WORLD_SIZE, WORLD_SIZE))
           for a in ACTIONS:
               s_, r = step(s, a) #输入状态和动作，返回下一个状态和奖励
               index_s_ = np.ravel_multi_index(s_, (WORLD_SIZE, WORLD_SIZE))
               A[index_s, index_s_] += ACTION_PROB * DISCOUNT
               b[index_s] -= ACTION_PROB * r
x = np.linalg.solve(A, b)

最后得到的结果如图3.4所示。

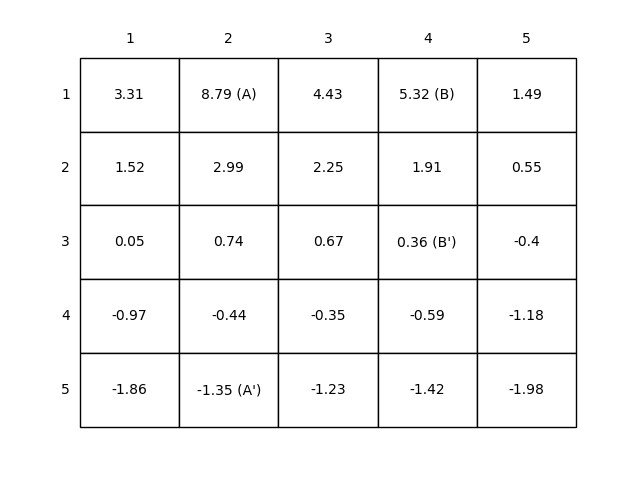
​ 图3.4 网格世界的状态价值函数

求解方式2：基于随机动作的策略，利用Bellman递推式，状态价值期望直至收敛

\[\begin{eqnarray*} v_\pi(s)&=&\mathbb{E}[G_t|S_t=s]\\ &=&\sum_a\pi(a|s)\left[r+\gamma v_\pi(s')\right] \end{eqnarray*} \]

采用同步的更新方式，即利用当前的状态价值函数，逐一更新每个状态的价值，得到新的状态价值函数。如果新的状态价值函数与当前的没有什么差异，则表示已经收敛，结束迭代。否则，继续前面操作。核心代码如下。

value = np.zeros((WORLD_SIZE, WORLD_SIZE))
while True:
    # keep iteration until convergence
    new_value = np.zeros_like(value)
    for i in range(WORLD_SIZE):
        for j in range(WORLD_SIZE):
            for action in ACTIONS:
                (next_i, next_j), reward = step([i, j], action)
                # bellman equation(核心部分)
                new_value[i, j] += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])
    if np.sum(np.abs(value - new_value)) < 1e-4:
        break
    value = new_value

最后得到的结果与图3.4所示相同。采用同步更新的方式，对初值不敏感，采用了多组初值都可以得到最终正确的结果。如果采用异步的更新方式，即只保存最新的状态价值函数，也可以得到同样的结果。核心代码如下。

# 只维护一份状态价值函数
value = np.ones((WORLD_SIZE, WORLD_SIZE))
while True:
    delta = 0
    # keep iteration until convergence
    for i in range(WORLD_SIZE):
        for j in range(WORLD_SIZE):
            temp = 0
            for action in ACTIONS:
                (next_i, next_j), reward = step([i, j], action)
                # bellman equation
                temp += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])
            delta = max(delta, np.abs(temp - value[i, j]))
            value[i, j] = temp
    if delta < 1e-4:
       break

在比较同步和异步两种更新方式的迭代次数时，发现同步更新需要迭代77轮，而异步更新只需要迭代47轮。因此，异步迭代速度更快。

求解方式3：基于贝尔曼最优公式，分别采用同步和异步的方式迭代更新状态价值函数。

这里给出异步方式的核心代码。

value = np.zeros((WORLD_SIZE, WORLD_SIZE))
k = 0
while True:
    delta = 0
    k += 1
    # keep iteration until convergence
    for i in range(WORLD_SIZE):
        for j in range(WORLD_SIZE):
            values = []
            for action in ACTIONS:
                (next_i, next_j), reward = step([i, j], action)
                # value iteration
                values.append(reward + DISCOUNT * value[next_i, next_j])
            new_value = np.max(values)
            delta = max(delta, np.abs(new_value - value[i, j]))
            value[i, j] = new_value
    if delta < 1e-4:
        print('k = {}'.format(k))
        break

经过比较，无论采用同步或者异步的方式， 都能得到一样的结果。如图3.5所示。但是可以发现采用异步迭代只需要遍历所有状态24轮，而采用同步迭代需要遍历124轮。

​ 同时，与上面实验对比发现基于贝尔曼最优公式的状态价值函数与基于期望的贝尔曼公式的状态价值函数，两者是不一样的。原因在于，它们所采取的策略是不同的，求解方式3中的策略是采用贪婪动作，而求解方式2中的策略是随机策略。这进一步说明，采用的策略不同，得到的状态价值函数也是不同的，但最优状态价值函数是相同的，与之对应的最优策略可以有多种。

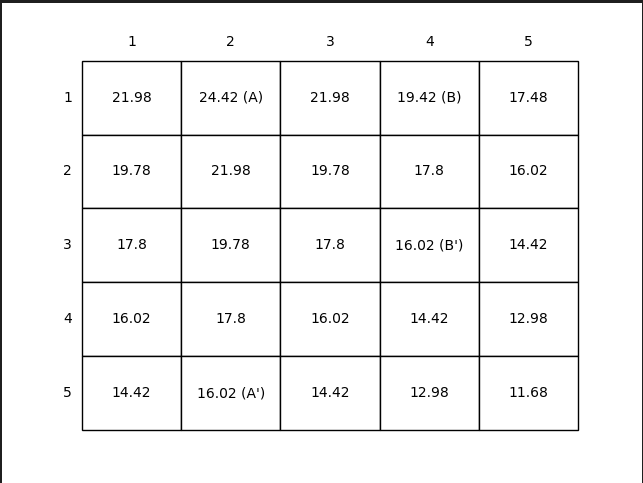
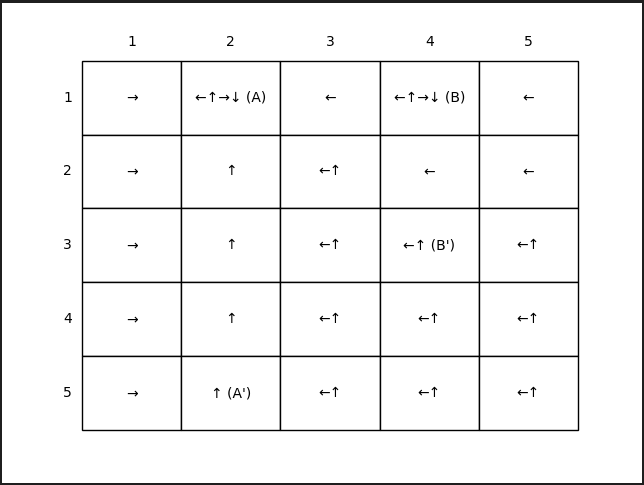
图3.5 左图展示了最优状态价值函数，右图展示了最优策略