强化学习读书笔记--第二章多臂bandits问题
第二章 多臂bandits问题
强化学习区别于其他机器学习范式的一个最重要的特征在于它利用训练过程中获得的经验去评估所采取的动作的好坏,而不是给定正确的动作去指导智能体学习。前者称之为评估反馈(evaluative feedback),后者称之为指导反馈(instructive feedback)。
问题描述:
\(k\)臂bandits问题,假设现在需要重复地从\(k\)个不同选择/动作中选择,在每次选择后都会收到一个数值奖励(奖励服从一个静态的概率分布)。现在的目标就是在规定的时间(time-step)内最大化这个累计奖励。
在这个问题中,每个动作有一个期望奖励值,称为该动作的价值(value)。记 \(t\) 时间采取的动作为\(A_t\),对应的奖励为\(R_t\),定义一个随机动作的真实期望价值为\(q_*(a)\):
在每一时刻必须在探索(exploration)和挖掘(exploitation)之间做出权衡。利用现有经验选择估计动作价值\(Q_t(A_t)\)最大的动作,这种方式称为挖掘或贪婪动作(greedy action)。选择估计动作价值非最大的动作,这种方式称为探索,因为从长远的角度来看,探索有利于获得更大的累积奖励。例如,当前的贪婪动作虽然估计价值是最大的,但其他动作的估计价值存在较大的不确定性,那么当前的贪婪动作就不一定是实际价值最大的动作。
\(\epsilon\)-greedy方法
给定一个超参数\(\epsilon\in(0,1]\),有\(\epsilon\)的概率选择探索,例如采取随机动作;有\(1-\epsilon\)的概率选择挖掘,即贪婪动作。当然,\(\epsilon\)可以是变化的,例如随着\(t\)的增加而逐渐减小。这也比较符合逻辑,在智能体经验不足的时候多探索环境,当经验丰富之后更多地挖掘动作的价值。
动作价值的估计\(Q_t(A_t)\)
A. 定步长估计方法
对于静态的\(k\)臂bandits问题,即每台bandit的奖励服从静态概率分布,可以推导出\(Q_t(A_t=a)\)的递推表达式,为了简化符号,令\(Q_n\)表示动作\(a\)的前\(n-1\)次奖励的期望,\(r_n\)表示第\(n\)次奖励的值。可得
注:这里利用一个技巧\(nQ_{n+1}=r_n+\sum_{i=1}^{n-1}r_i=r_n+(n-1)Q_n\)。
对于动态的\(k\)臂bandits问题,即奖励的概率分布会随着时间发生变化。因此,式(2.1)采用加权平均的方式并不能很好的处理。更合理的处理方式是给近期的奖励更高的权重,而给越久远的奖励分配越小的权重。扩展(2.1)为
当\(\alpha=1\)时,\(Q_{n+1}=r_n\),即动作价值估计只参考当前的奖励值。\(\alpha\)越大,则表示动作价值估计越看重近期的奖励。将式(2.2)进一步展开可以看出\(Q_{n+1}\)本质是所有历史奖励的加权和:
\(Q_1\)是人为设定的初始值。当设置\(Q_1=0\),这符合正常逻辑,毕竟一开始都没有参考的经验。但初值设置偏大,采取贪婪策略,即每次选择当前最佳动作,也会起到很好的效果。因为当实际获得的奖励\(r_t\)小于估计价值,智能体就更倾向于选择其他动作(\(Q_{t+1}减小\)),这样同样起到了促进智能体积极探索环境的目的。但这种初始化方法只适用静态问题。
B. 样本平均估计方法
利用每一个动作在游戏中所获得的奖励,更新每个动作的平均奖励:
注:两种估计动作价值的方法差异在于A方法是定步长,B方法是随着样本的增加\(n\)不断增加。
UCB1方法
UCB全称为置信上界(upper confidence bound),同样也是一种均衡探索和挖掘的方法:
其中,\(t\)为智能体与环境交互的总次数,\(N_t(a)\)表示在\(t\)之前动作\(a\)被选择的次数,\(Q_t(a)\)表示动作\(a\)在\(t\)时刻的价值估计。在\(t\)较小时,使得智能体更倾向于选择不确定性较大的动作,而当\(t\)逐渐增大,动作价值估计也逐渐稳定,使得智能体更倾向于选择价值最高的动作。由此也可以看出,UCB1方法适用于静态问题,而不适用非静态问题。
梯度bandit算法
与UCB1方法类似,梯度bandit算法(gradient bandit algorithms)同样是从估计动作价值出发选择最高估计价值的动作。不同在于,梯度bandit算法构造期望奖励的准则函数,通过沿梯度方向最大化期望奖励。
考虑给每个动作\(a\)进行打分记为\(H_t(a)\),利用softmax获得每个动作的概率分布:
构造准者函数
其中,\(q_*(x)\)表示动作\(x\)的真实动作价值(实际是不可获取的)。
将式(2.4)对\(H_t(a)\)求偏导可得
前面的推导过程,利用了\(q_*(x)\)为常数,并引入基准\(B_t\)(baseline)(不影响求解方向梯度)。利用\(q_*(x)=E[R_t|x]\)和蒙特卡洛近似,将\(r_t\)代替\(q_*(x)\),可以通过历史经验得到的动作价值期望设置\(B_t=\bar{R}_t\)。利用式(2.3)可得
沿着梯度方向更新\(H_t(x)\),可以最大化准则函数(2.4)。
值得一提的是,引入基准\(B_t\)虽然不会影响梯度方向,但是却能有效降低更新数据的方差,从而使得收敛更加平稳迅速。
实验
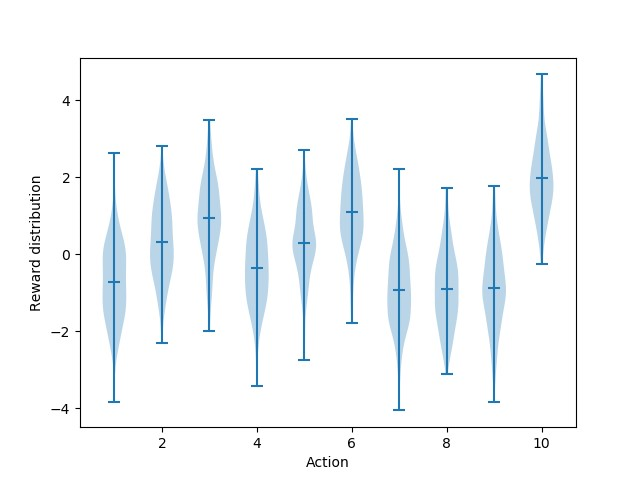
设计多臂bandits游戏,共有10台bandits,bandits的奖励均值服从\(U_i\sim\mathcal{N}(0,1)\),每台bandit的奖励服从\(R_i\sim\mathcal{N}(U_i,1)\),图2.1绘制bandits的奖励箱线图。下面的所有实验为了体现一般性,采用蒙特卡洛仿真方法,游戏总共2000轮,每轮进行1000步。
实验1:epsilon-greedy策略下的bandits平均奖励和最优动作选择率
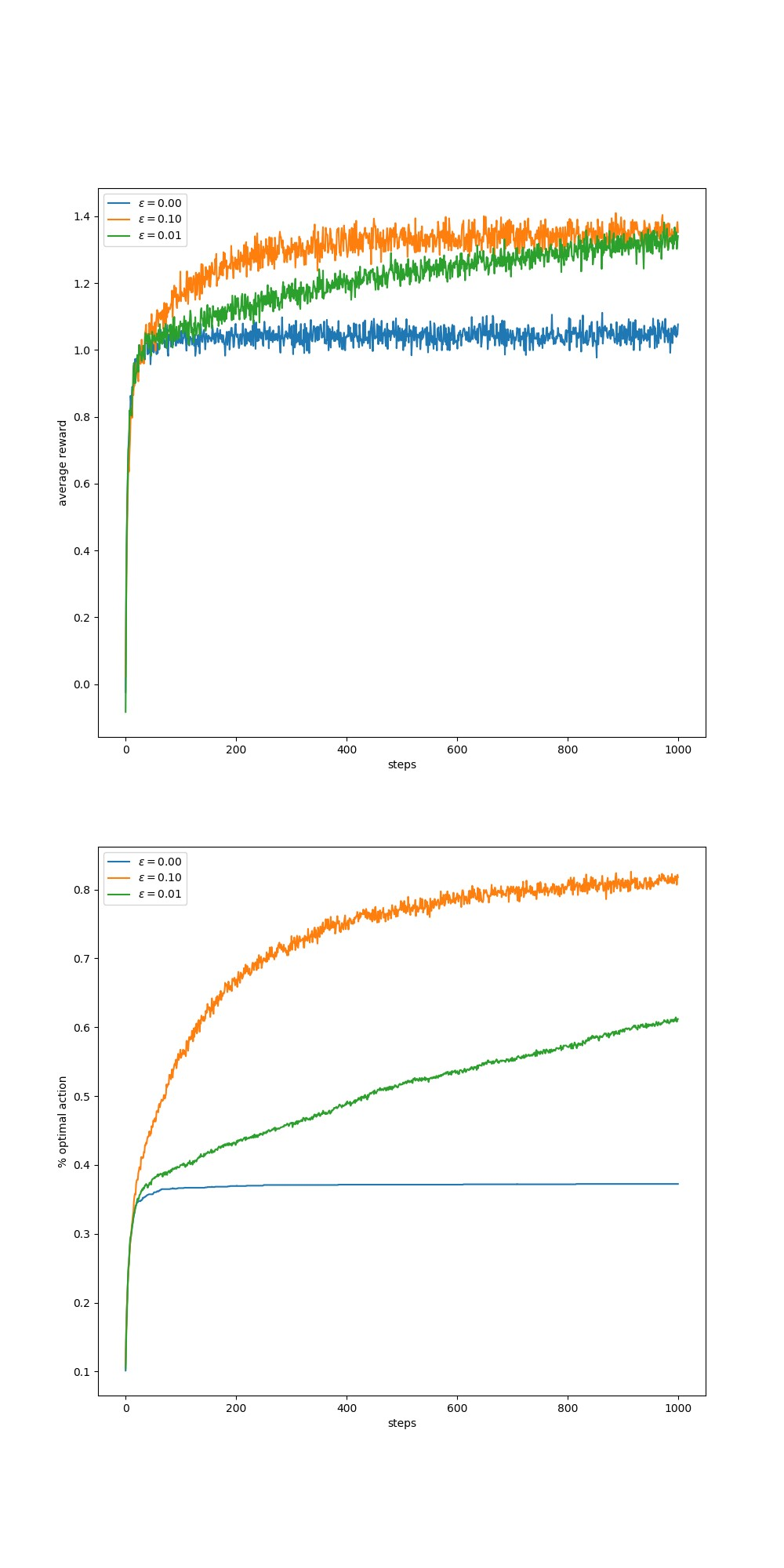
可以看出试错学习优于贪婪策略,\(\epsilon\)较大有利于找到最优动作,但是当试错次数足够多以后,\(\epsilon\)不缩小则会影响最优动作的选择率。
实验2:乐观估计初值和正常初值下的bandits奖励曲线比较
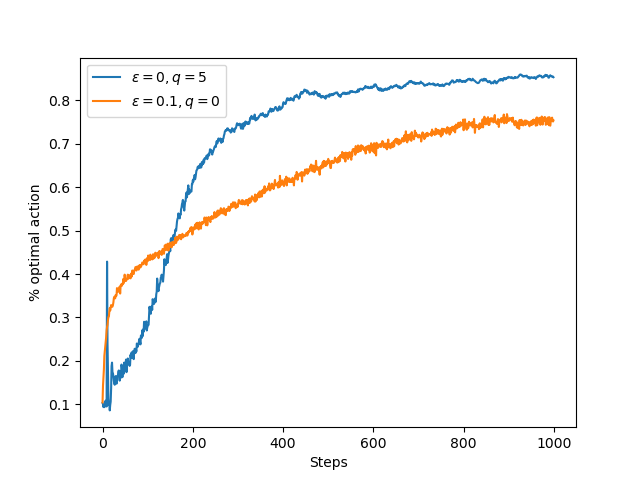
这里可以看出采用乐观的初值估计,在采用贪婪动作的情况下同样能够促进智能体探索新的动作(因为实际动作不满足估计的初值)。乐观估计的初值之所以会出现尖峰,在于前十次尝试的奖励必然都不满足初值,所以动作选择是随机的,到第11次则会有较大概率选择最优策略,但依然不满足初值。由此,产生尖峰。
实验3:UCB1策略和epsilon-greedy策略的bandits奖励比较
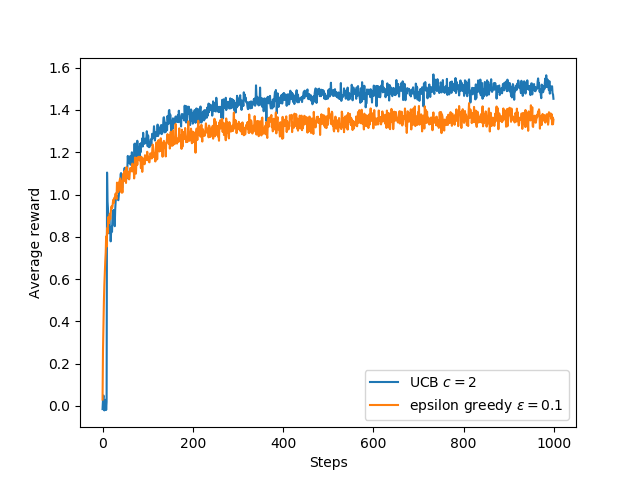
这里可以看出UCB1策略优于\(\epsilon\)-greedy策略,同样会在第11步的时候产生尖峰,原因与实验2相同。UCB1策略能够更快的收敛到最优动作。
实验4:gradient bandit algorithm的bandits奖励比较
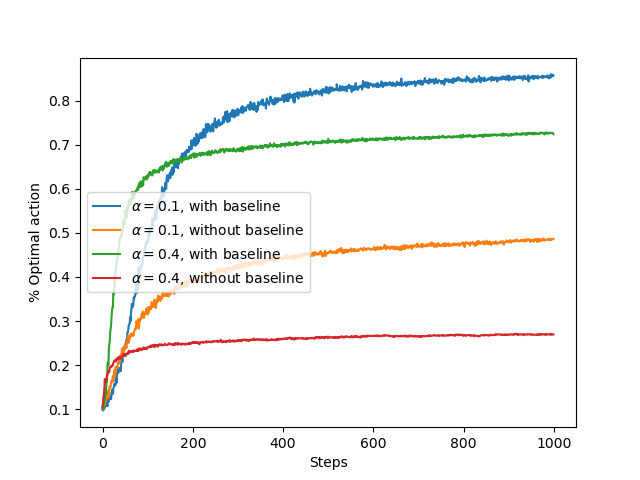
可以看出采用baseline的方法优于不用baseline的方法,其原因在于引入baseline能有效降低更新数据的方差,从而使得收敛更加平稳迅速。另外学习率不易过大,会导致算法在最优动作附近不断徘徊。
实验5:比较\(\epsilon\)-greedy策略、gradient-bandit策略、UCB1策略和乐观初值估计策略等四类策略对各自超参数的敏感程度
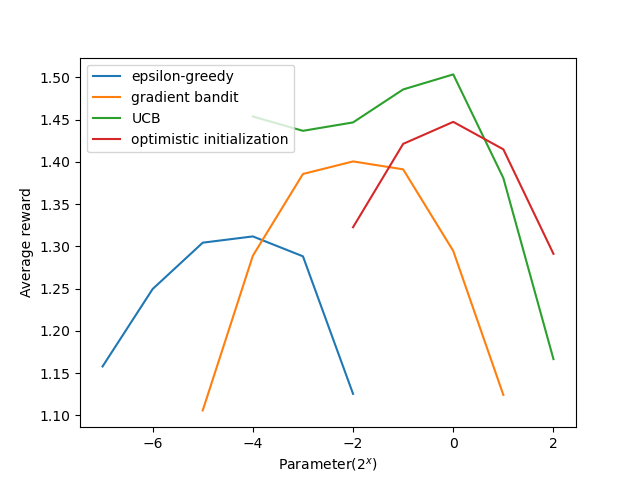
可以看出UCB1策略对初始敏感度最低(在很广的范围内性能保持良好),其他几种策略需要进行调参。
程序实现
具体代码参照随书代码ten_armed_testbed.py。这里大致介绍一下代码实现的逻辑框架。
首先构建游戏架构,这里封装在Bandit类中,游戏过程封装在函数simulate中。其中,Bandit类封装了如下几个功能。
reset()用于重置游戏act()选择一个动作,即选择一台bandit进行操作step()给定一个动作,返回其奖励,并更新动作价值估计列表
整体代码比较简单,但逻辑结构很巧妙。超参数较多,仔细阅读并不难懂,这里就不再赘述了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号