图像分割系列:Normalized Cuts and Image Segmentation论文解析
图像分割系列:Normalized Cuts and Image Segmentation论文解析
论文作者简介
Jianbo Shi出生于上海,本科就读于康奈尔大学计算机科学与数学专业,1994年获学士学位。其后就读于加州大学伯克利分校计算机科学专业,1998年获得博士学位,博士论文为Normalize Cuts Image Segmentation algorithm。1999年到卡耐基梅隆大学机器人研究所担任研究员。2003年加入宾夕法尼亚大学计算机与信息科学系,现任教授。其研究领域包括图像/视频检索,计算机视觉,机器智能等。
问题背景
图像分割领域中,将一幅图像分割成为几部分可以有很多可能的方式,判断何种方式分割是正确的,是图像分割的核心问题。这个问题存在两个方面,一个方面是分割方式并非唯一解,往往需要有先验知识。先验知识包含一些低阶的特征,比如明亮度、颜色、纹理或运动等,也包含中阶或者高阶的知识,比如物体形状或物体对称性等等。另一方面图像分割本身是具有层次性的,图像可以构造树状结构进行层次分割。因此,基于低阶先验知识的分割通常无法得到最终期望的目标分割结果。
一般而言,低阶特征适合将图像分割成基础小块,即最低层次分割。中阶或高阶特征用于组合基础小块并挑选出值得关注的部分,可以进一步进行再分割和分组。
本论文基于图理论架构进行分组。将每一个像素点作为图中的顶点。在某一个特征空间下,用两两像素点间的特征关系构成图中的边。那么,图像分割问题就变成了图分割问题,将所有顶点分割成不连接的数个顶点集\(V_1, V_2, \cdots, V_m\),其衡量标准是顶点集内相似度高,不同顶点集之间相似度低。
方法定义
定义加权图\(G=(V,E)\),可以分割成为两个子集\(\{A,B\}\),其中\(A\cap B=\empty\),\(A\cup B=V\)。每个像素作为顶点\(u,v\in V\),每条边\(e\in E\)用于衡量顶点两两之间的相似度\(w(u,v)\)。图分割的定义为
显然,考虑让不同子图之间相似度最小化,即最小化\(cut(A,B)\)。但是,文章中也指出采用这样的准则函数,往往只能将一些孤立点分割出来,原因是若集合\(A\)和\(B\)之间的边越多,则\(cut(A,B)\)的值难以保证是极小值,图1所示。
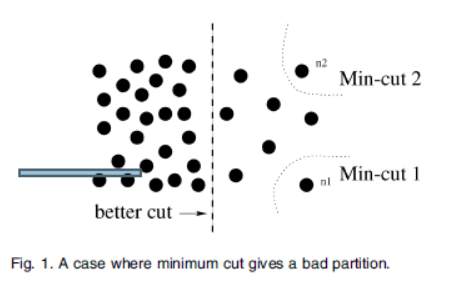
因此,作者提出一种规范化的图分割,
在此定义下,孤立点的分割无法使得准则函数\(Ncut(A,B)\)取极小值,解决了传统\(cut\)方法的问题。在二类分割问题中,Ncut方法能将同时满足两个不同顶点集之间相似度极小化,且同一顶点集内相似度极大化。文中进行了证明,简写如下。
说明:\(assoc(A,A)\)和\(cut(A,A)\)在数学定义上并没有什么区别,只是目的上有所区别。
准则函数
为方便后面算法的实现,先定义一些变量。定义\(x\in\R^N\)为指示向量,其中\(x_i=1\)表示第\(i\)个顶点属于集合\(A\),\(x_i=-1\)表示属于集合\(B\),\(|V|=N\)。定义权值矩阵\(W\in\R^{N\times N}\),其中\(W(i,j)=w_{ij}\)。定义\(d_i=\sum_jW(i,j)\)为顶点\(i\)与所有顶点的连接和。定义\(D\in\R^{N\times N}\)为对角阵,其中对角元素为\(d_i\),\(D=W\cdot 1_{N\times1}\)。
下面逐一分析\(Ncut(A,B)\)各项的数学形式。
-
\(x_1\)和\(x_2\)
\(x_1=\frac{1+x}{2}\)可以看作集合\(A\)的指示向量,属于\(A\)为1,不属于为0。\(x_2=\frac{1-x}{2}\)可以看作集合\(B\)的指示向量,属于\(B\)为\(1\),不属于为0。
说明:作为读者肯定会觉得为何不在\(x\)的定义中就采用这样的方式呢,例如属于\(A\)的指示向量为\(x_1\),向量中只有0和1两个元素。属于\(B\)的指示向量为\(x_2\)。这样方便后面计算。事实上在Shi Jianbo后续的文章中,的确做了这样的修改。
-
\(assoc(A,V)\)
\[\begin{eqnarray*} assoc(A,V)&=&\sum_{u\in A,v\in V}W(u,v)=\sum_{x_i>0}d_i\\ &=&x_1^TDx_1 = \frac{1}{4}(1+x)^TD(1+x)\\ \end{eqnarray*} \] -
\(assoc(B,V)\)
同理可得
\[assoc(B,V)=\frac{1}{4}(1-x)^TD(1-x) \] -
\(assoc(A,A)\)
\[\begin{eqnarray*} assoc(A,A) &=& \sum_{u\in A,v\in A}W(u,v)\\ &=& x_1^TWx_1 = \frac{1}{4}(1+x)^TW(1+x) \end{eqnarray*} \] -
\(assoc(B,B)\)
同理可得
\[assoc(B,B) = \frac{1}{4}(1-x)^TW(1-x) \] -
\(cut(A,B)\)
\[\begin{eqnarray*} cut(A,B) &=& \sum_{u\in A,v\in B}W(u,v) = assoc(A,V)-assoc(A,A)\\ &=& \frac{1}{4}(1+x)^TD(1+x)-\frac{1}{4}(1+x)^TW(1+x)\\ &=&\frac{1}{4}(1+x)^T(D-W)(1+x) \end{eqnarray*} \]其另一种表达形式为
\[\begin{eqnarray*} cut(A,B) &=& assoc(B,V)-assoc(B,B)\\ &=& \frac{1}{4}(1-x)^TD(1-x)-\frac{1}{4}(1-x)^TW(1-x)\\ &=&\frac{1}{4}(1-x)^T(D-W)(1-x) \end{eqnarray*} \] -
\(Ncut(A,B)\)
采用上面的形式可得
\[\begin{eqnarray*} Ncut(A,B) &=& \frac{(1+x)^T(D-W)(1+x)}{(1+x)^TD(1+x)}+\frac{(1-x)^T(D-W)(1-x)}{(1-x)^TD(1-x)}\\ &=&\sum_{i=1,2}\frac{x_i^T(D-W)x_i}{x_i^TDx_i}\tag{1} \end{eqnarray*} \]虽然式(1)中存在两个离散向量,但还是在瑞利商的框架下,可以通过求解广义特征向量进行优化。在本论文当中,作者将其化为关于指示向量\(x\)的准则函数:
\[\min_x Ncut(x) = \min_y \frac{y^T(D-W)y}{y^TDy}\tag{2} \]其中,\(y=(1+x)-b(1-x)\),
\[b = \frac{\sum_{x_i>0}d_i}{\sum_{x_i<0}d_i}。 \]不得不说,作者的数学基础非常扎实。由此,可得\(y(i)\in\{1,-b\}\),可见\(b\)的浮动范围还是挺大的。
简单说一下,如何从式(1)得到式(2)这样统一的表达形式,不能只是简单的通分。分析一下\((1+x)^TD(1+x)\):
\[\begin{eqnarray*} &&(1+x)^TD(1+x)\\ &=&1^TD1+2x^TD1+x^TDx\\ &=&\left(\sum_{x_i>0}d_i+\sum_{x_i<0}d_i\right)+2\left(\sum_{x_i>0}d_i-\sum_{x_i<0}d_i\right)+\left(\sum_{x_i>0}d_i+\sum_{x_i<0}d_i\right)\\ &=&4\sum_{x_i>0}d_i \end{eqnarray*} \]同理可得
\[(1-x)^TD(1-x)=4\sum_{x_i<0}d_i \]由此,作者引入一个参数\(k\),从而方便算式进行通分。
\[k = \frac{\sum_{x_i>0}d_i}{\sum_id_i} \]从而可得
\[\begin{eqnarray*} (1+x)^TD(1+x)&=&4k\cdot 1^TD1\\ (1-x)^TD(1-x)&=&4(1-k)\cdot 1^TD1\\ \end{eqnarray*} \]
算法实现
构建准则函数,其核心在于构建加权图\(G=(V,E)\),针对不同的情况设计权值\(w_{ij}\)的计算方法,考虑两个方面一是顶点之间的相似性,二是顶点之间的空间距离。
详细分析一下式(3),函数\(F(i)\)根据待分割图像的实际情况选择不同的表达式,表示顶点\(i\)的特征值或特征向量,\(\sigma_I\)用于控制不同顶点之间相似度的容忍度。\(X(i)\)表示顶点\(i\)的空间坐标,\(\sigma_X\)用于控制不同顶点之间空间相似度的容忍度。作者建议\(\sigma\)的选值范围可以是这个距离浮动范围的\(10\%\)到\(20\%\)。
- 选择\(F(i)=\{1,0\}\),用于分割点集合或二值图。
- 选择\(F(i)=I(i)\),\(I(i)\)表示图像中顶点\(i\)的像素值,用于分割灰度图。
- 选择\(F(i)=[v,v\cdot s\cdot \sin(h),v\cdot s\cdot \cos(h)](i)\),其中\(h,s,v\)为HSV空间中的值,用于颜色分割。当然也可以选择RGB空间。、
- 选择\(F(i)=[|I*f_1|,|I*f_2|,\ldots,|I*f_n|](i)\),其中\(f_i\)为DOOG滤波器组包含不同尺度和方向,用于纹理分割。
当然,权值函数\(w(i,j)\)的选择需要根据具体的问题去设计才能获得较好的分割结果。设计好权值函数就可以计算并构建权值矩阵\(W\),从而得到准则函数,并设计优化方法。
优化准则函数
将\(y\)放宽条件到实数域,那么可以利用广义瑞利商的结论进行优化。由瑞利商的性质易得,\(D^{-1}(D-W)\)矩阵肯定含有一个特征值为0且对应特征向量为\(1_N\)。同时,利用施密特正交化可以保证特征空间中,特征向量之间两两正交。因此,第二特征向量必然与\(1_N\)正交,条件\(y^TD1=0\)在广义瑞利商的框架下必然成立,且第二特征向量为该准则函数的解\(y\),所对应的特征值为准则函数的最小值。
说明:\(D^{-1}(D-W)\)和\(D^{-1/2}(D-W)D^{-1/2}\)的特征向量之间的关系为\(x_{前}=D^{-1/2}x_后\)。
作者提出两种思路来进行图像分割,一种是递归方法(recursive two-way ncut),进行多次分割,每次只分割成两部分。另一种是一次完成分割(simultanous K-way cut with multiple eigenvectors),在优化准则函数的过程中,一次取前\(n\)个特征向量,即每个顶点的特征为一个\(n\)维的向量。对于一次分割,作者建议先聚类成\(k'\)个类,然后逐步进行合并,直到只有\(k\)个类为止,\(k'>k\)。
说明:K-way cut应该只在理论层面可行,因为图像较大导致\(D-W\)是一个超高维稀疏矩阵,在求解其前\(n\)个最小特征向量的过程中,不会采用求解所有的特征向量的方法,原因很明显,计算量太大了且大部分特征向量并不需要。因此,会采用Lanczos算法去估计部分特征向量。但Lanczos算法的缺点是会随着\(n\)的增大,而越发不准确。
下面我们还需要讨论一个细节,以分割成两部分为例,因为是将\(y\)放宽至实数域进行分割的,因此还需要将\(y\)进行离散化(二值化),需要选择一个合适的分割点。可以有下面几种方法。
-
取0为分割点。从理论层面讲,\(y\)的理论值为\(\{1,-b\},\ b>0\),因此理论上取0应该可以分割正确。但是由于实际过程中,图像存在噪声,估计的特征向量存在误差,以及权值函数的设计存在问题等等情况,因此分割点0将不再准确。
-
采用直方图的方法,比如利用OTSU方法求取分割点。因为前景与背景之间往往方差较大,物体内部的方差较小。
-
遍历搜索方法。从Ncut的标准出发,搜索分割点使得
\[Ncut(A,B) = \frac{cut(A,B)}{assoc(A,V)}+\frac{cut(B,A)}{assoc(B,V)} \]最小。搜索范围和搜索精度可以人为设定,这样可以有效提高搜索效率。
实验与仿真
因为篇幅所限,实验和仿真会发布,有兴趣的读者可以自行前往。论文作者也提供了MATLAB版本的实验,但存在版本问题和一些bug,我也已经都进行了修改,目前可以正常运行在2018b的版本。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号