数学系列： 施密特正交化（含实现代码）

前置概念

在理解施密特正交化之前，需要先理解几个概念。

• 什么是正交向量组？

  正交向量组是指内积为零的两个或者多个非零向量所构成的向量组。如果存在两个向量\(\alpha\)和\(\beta\)，满足\(<\alpha,\beta>=\alpha^T\beta=0\)，则称这两个向量正交，可记作\(\alpha\bot\beta\)。正交向量组内的向量两两正交。

• 什么是标准正交向量？

  标准正交向量是在满足正交向量的条件下，向量的模为1，即正交向量\(\|\alpha\|=1\)。

• 向量\(b\)在向量\(a\)上的投影值是多少?投影向量是什么？

  

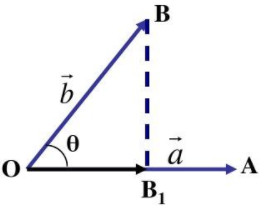  图1 向量b在a上得到投影

  ​ 图1展示了两向量投影的物理过程，由该过程可得

  \[\|OB_1\|=\|b\|\cos\theta=\|b\|\frac{<b,a>}{\|a\|\cdot\|b\|}=\frac{<b,a>}{\|a\|}。 \]

  我们可以换个思路，一个向量\([a_1,a_2]\)可以看作在标准正交向量\(e_1=[1,0]\)方向的坐标为\(a_1\)，在\(e_2=[0,1]\)方向的坐标为\(a_2\)。也可以理解为在相应轴上的投影。由此，向量\(b\)在向量\(a\)方向上的坐标为

  \[\|OB_1\|=<b,\frac{a}{\|a\|}>=\frac{<b,a>}{\|a\|}。 \]

  可以看出，这两个过程等价。投影向量即投影值\(\times\)该方向的单位向量，可得

  \[\overrightarrow{OB_1}=\|OB_1\|\frac{a}{\|a\|}=\frac{<b,a>}{\|a\|^2}a。 \]

  另外，值得注意的\(\overrightarrow{OB}-\overrightarrow{OB_1}\)可以得到一个与向量\(a\)正交的向量\(\overrightarrow{B_1B}\)。

施密特正交化

​ 有了前面几个概念为基础，可以进一步理解施密特正交化。施密特正交化（Schmidt orthogonalization）是在欧氏空间中求一组正交基的方法。假设在欧式空间存在一线性无关的向量组\((\alpha_1,\alpha_2,\ldots,\alpha_n)\)，将该组向量进行标准正交化得到标准正交向量组\((\beta_1,\beta_2,\ldots,\beta_n)\)，这种方法称为施密特正交化。

​ 施密特正交化的步骤如下：

• \(\beta_1=\alpha_1\)，并对向量\(\beta_1\)进行标准化，得到\(\beta_1=\frac{\beta_1}{\|\beta_1\|}\)。

• 标准正交化\(\alpha_2\)，使其与\(\beta_1\)正交，即\(\alpha_2\)减去其在\(\beta_1\)上的投影向量：

  \[\beta_2 = \alpha_2-\frac{\alpha_2^T\beta_1}{\|\beta_1\|^2}\beta_1=\alpha_2-\alpha_2^T\beta_1\beta_1, \]

  然后对\(\beta_2\)进行标准化，得到\(\beta_2=\frac{\beta_2}{\|\beta_2\|}\)。

• 标准正交化\(\alpha_3\)，使其与\(\beta_1\)和\(\beta_2\)同时正交，即\(\alpha_3\)减去其在\(\beta_1\)和\(\beta_2\)上的分别投影向量：

  \[\beta_3 = \alpha_3-\alpha_3^T\beta_1\beta_1-\alpha_3^T\beta_2\beta_2 \]

  然后对\(\beta_3\)进行标准化，得到\(\beta_3=\frac{\beta_3}{\|\beta_3\|}\)。

• 由此进行递归，直至将\(\alpha_n\)进行标准正交化：

  \[\beta_n = \alpha_n-\sum_{i=1}^{n-1}\alpha_n^T\beta_i\beta_i \]

  然后对\(\beta_n\)进行标准化，得到\(\beta_n=\frac{\beta_n}{\|\beta_n\|}\)。

由上述步骤，得到一组标准正交向量组\((\beta_1,\beta_2,\ldots,\beta_n)\)。

程序实现（MATLAB）

仿真过程：给定任意一个矩阵\(A\in\R^{m\times n}\)，其中\(A=[a_1,a_2,\ldots,a_n]\)，\(m\geq n\)，\(rank(A)=n\)，通过施密特正交化得到标准正交向量组\(B=[\beta_1,\beta_2,\ldots,\beta_n]\in\R^{m\times n}\)。

function B = schmidt(A)
%施密特正交化
%    输入：
%        A -- m x n的矩阵，m>=n，rank(A)=n
%    输出：
%        B -- m x n的矩阵，施密特正交化后的结果

M = A;
[m,n] = size(A);
if m<n
    error('schmidt:wrong dimension of matrix A!');
end
if rank(A)<n
    error('schmidt: matrix A is not full column rank!');
end
M(:,1) = A(:,1)/norm(A(:,1));
for i=2:n
    for j=1:i-1
        M(:,i) = M(:,i)-A(:,i)'*M(:,j)*M(:,j);
    end
    M(:,i) = M(:,i)/norm(M(:,i));
end
B = M;
end


%main%
m = 10;
n = 5;
while(true)
    A = randn(m,n);
    if rank(A)==n
        break
    end
end

B = schmidt(A);
disp('施密特正交化后的正交向量组为:')
B