卷积神经网络中的卷积核真的仅仅在挪动?
卷积神经网络中的卷积核真的仅仅在挪动?
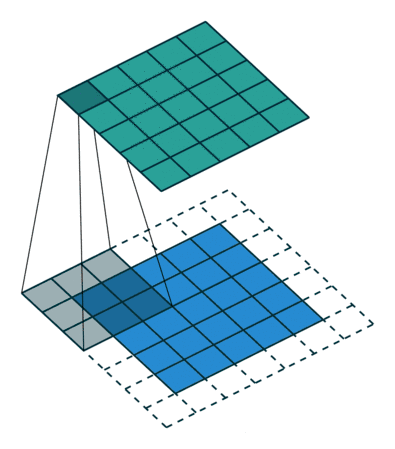
卷积神经网络中的卷积核
初等概率论中卷积公式
一维
连续
\[(f*g)(\tau)=\int_{-\infty}^{\infty}f(t)\cdot g(\tau-t)dt
\]
二维
连续
\[(f*g)(\tau_1,\tau_2)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t_1,t_2)\cdot g(\tau_1-t_1,\tau_2-t_2)dt
\]
离散
\[(f*g)(\tau_1,\tau_2)=\sum_{i=-\infty}^{\infty}\sum_{j=-\infty}^{\infty}f(i,j)\cdot g(\tau_1-i,\tau_2-j)
\]

例子
考虑二维情况计算
\[f=\left[\begin{array}{rrrr}
1 & 2 & 3 & 4 \\
5 & 6 & 7 & 8 \\
9 & 10 & 11 & 12 \\
13 & 14 & 15 & 16 \\
\end{array}\right]
\]
和
\[g=\left[\begin{array}{rr}
-3 & 1 \\
4 & -2
\end{array}\right]
\]
问:如何计算f和g的卷积?
具体计算如下
方法一
使用全面的离散情况公式进行计算
\[(f*g)(\tau_1,\tau_2)=\sum_{i=-\infty}^{\infty}\sum_{j=-\infty}^{\infty}f(i,j)\cdot g(\tau_1-i,\tau_2-j)
\]
于是有 (简单起见,取 f 和 g的最大支撑集进行计算)
\[(f*g)(\tau_1,\tau_2)=\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(\tau_1-i,\tau_2-j)
\]
这样,就得到(为使计算过程更加清晰,下面计算过程尽量不作约简)
\[\begin{array}{ll}
&(f*g)(0,0) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(0-i,0-j)\\
=& f(0,0)\cdot g(0-0,0-0)+f(0,1)\cdot g(0-0,0-1)+f(0,2)\cdot g(0-0,0-2)+f(0,3)\cdot g(0-0,0-3)\\
&+ f(1,0)\cdot g(0-1,0-0)+f(1,1)\cdot g(0-1,0-1)+f(1,2)\cdot g(0-1,0-2)+f(1,3)\cdot g(0-1,0-3)\\
&+ f(2,0)\cdot g(0-2,0-0)+f(2,1)\cdot g(0-2,0-1)+f(2,2)\cdot g(0-2,0-2)+f(2,3)\cdot g(0-2,0-3)\\
&+ f(3,0)\cdot g(0-3,0-0)+f(3,1)\cdot g(0-3,0-1)+f(3,2)\cdot g(0-3,0-2)+f(3,3)\cdot g(0-3,0-3)\\
=& f(0,0)\cdot g(0-0,0-0)\\
=& f(0,0)\cdot g(0,0)\\
=& 1\cdot -3\\
=& -3
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(0,1) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(0-i,1-j)\\
=& f(0,0)\cdot g(0-0,1-0)+f(0,1)\cdot g(0-0,1-1)+f(0,2)\cdot g(0-0,1-2)+f(0,3)\cdot g(0-0,1-3)\\
&+ f(1,0)\cdot g(0-1,1-0)+f(1,1)\cdot g(0-1,1-1)+f(1,2)\cdot g(0-1,1-2)+f(1,3)\cdot g(0-1,1-3)\\
&+ f(2,0)\cdot g(0-2,1-0)+f(2,1)\cdot g(0-2,1-1)+f(2,2)\cdot g(0-2,1-2)+f(2,3)\cdot g(0-2,1-3)\\
&+ f(3,0)\cdot g(0-3,1-0)+f(3,1)\cdot g(0-3,1-1)+f(3,2)\cdot g(0-3,1-2)+f(3,3)\cdot g(0-3,1-3)\\
=& f(0,0)\cdot g(0-0,1-0)+f(0,1)\cdot g(0-0,1-1)\\
=& f(0,0)\cdot g(0,1)+f(0,1)\cdot g(0,0)\\
=& 1\cdot 1+2\cdot -3\\
=& -5
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(0,2) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(0-i,2-j)\\
=& f(0,0)\cdot g(0-0,2-0)+f(0,1)\cdot g(0-0,2-1)+f(0,2)\cdot g(0-0,2-2)+f(0,3)\cdot g(0-0,2-3)\\
&+ f(1,0)\cdot g(0-1,2-0)+f(1,1)\cdot g(0-1,2-1)+f(1,2)\cdot g(0-1,2-2)+f(1,3)\cdot g(0-1,2-3)\\
&+ f(2,0)\cdot g(0-2,2-0)+f(2,1)\cdot g(0-2,2-1)+f(2,2)\cdot g(0-2,2-2)+f(2,3)\cdot g(0-2,2-3)\\
&+ f(3,0)\cdot g(0-3,2-0)+f(3,1)\cdot g(0-3,2-1)+f(3,2)\cdot g(0-3,2-2)+f(3,3)\cdot g(0-3,2-3)\\
=& f(0,1)\cdot g(0-0,2-1)+f(0,2)\cdot g(0-0,2-2)\\
=& f(0,1)\cdot g(0,1)+f(0,2)\cdot g(0,0)\\
=& 2\cdot 1+3\cdot -3\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(0,3) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(0-i,3-j)\\
=& f(0,0)\cdot g(0-0,3-0)+f(0,1)\cdot g(0-0,3-1)+f(0,2)\cdot g(0-0,3-2)+f(0,3)\cdot g(0-0,3-3)\\
&+ f(1,0)\cdot g(0-1,3-0)+f(1,1)\cdot g(0-1,3-1)+f(1,2)\cdot g(0-1,3-2)+f(1,3)\cdot g(0-1,3-3)\\
&+ f(2,0)\cdot g(0-2,3-0)+f(2,1)\cdot g(0-2,3-1)+f(2,2)\cdot g(0-2,3-2)+f(2,3)\cdot g(0-2,3-3)\\
&+ f(3,0)\cdot g(0-3,3-0)+f(3,1)\cdot g(0-3,3-1)+f(3,2)\cdot g(0-3,3-2)+f(3,3)\cdot g(0-3,3-3)\\
=& f(0,2)\cdot g(0-0,3-2)+f(0,3)\cdot g(0-0,3-3)\\
=& f(0,2)\cdot g(0,1)+f(0,3)\cdot g(0,0)\\
=& 3\cdot 1+4\cdot -3\\
=& -9
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(0,4) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(0-i,4-j)\\
=& f(0,0)\cdot g(0-0,4-0)+f(0,1)\cdot g(0-0,4-1)+f(0,2)\cdot g(0-0,4-2)+f(0,3)\cdot g(0-0,4-3)\\
&+ f(1,0)\cdot g(0-1,4-0)+f(1,1)\cdot g(0-1,4-1)+f(1,2)\cdot g(0-1,4-2)+f(1,3)\cdot g(0-1,4-3)\\
&+ f(2,0)\cdot g(0-2,4-0)+f(2,1)\cdot g(0-2,4-1)+f(2,2)\cdot g(0-2,4-2)+f(2,3)\cdot g(0-2,4-3)\\
&+ f(3,0)\cdot g(0-3,4-0)+f(3,1)\cdot g(0-3,4-1)+f(3,2)\cdot g(0-3,4-2)+f(3,3)\cdot g(0-3,4-3)\\
=& f(0,3)\cdot g(0-0,4-3)\\
=& f(0,3)\cdot g(0,1)\\
=& 4\cdot 1\\
=& 4
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(1,0) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(1-i,0-j)\\
=& f(0,0)\cdot g(1-0,0-0)+f(0,1)\cdot g(1-0,0-1)+f(0,2)\cdot g(1-0,0-2)+f(0,3)\cdot g(1-0,0-3)\\
&+ f(1,0)\cdot g(1-1,0-0)+f(1,1)\cdot g(1-1,0-1)+f(1,2)\cdot g(1-1,0-2)+f(1,3)\cdot g(1-1,0-3)\\
&+ f(2,0)\cdot g(1-2,0-0)+f(2,1)\cdot g(1-2,0-1)+f(2,2)\cdot g(1-2,0-2)+f(2,3)\cdot g(1-2,0-3)\\
&+ f(3,0)\cdot g(1-3,0-0)+f(3,1)\cdot g(1-3,0-1)+f(3,2)\cdot g(1-3,0-2)+f(3,3)\cdot g(1-3,0-3)\\
=& f(0,0)\cdot g(1-0,0-0)\\
&+ f(1,0)\cdot g(1-1,0-0)\\
=& f(0,0)\cdot g(1,0)\\
&+ f(1,0)\cdot g(0,0)\\
=& -11
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(1,1) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(1-i,1-j)\\
=& f(0,0)\cdot g(1-0,1-0)+f(0,1)\cdot g(1-0,1-1)+f(0,2)\cdot g(1-0,1-2)+f(0,3)\cdot g(1-0,1-3)\\
&+ f(1,0)\cdot g(1-1,1-0)+f(1,1)\cdot g(1-1,1-1)+f(1,2)\cdot g(1-1,1-2)+f(1,3)\cdot g(1-1,1-3)\\
&+ f(2,0)\cdot g(1-2,1-0)+f(2,1)\cdot g(1-2,1-1)+f(2,2)\cdot g(1-2,1-2)+f(2,3)\cdot g(1-2,1-3)\\
&+ f(3,0)\cdot g(1-3,1-0)+f(3,1)\cdot g(1-3,1-1)+f(3,2)\cdot g(1-3,1-2)+f(3,3)\cdot g(1-3,1-3)\\
=& f(0,0)\cdot g(1-0,1-0)+f(0,1)\cdot g(1-0,1-1)\\
&+ f(1,0)\cdot g(1-1,1-0)+f(1,1)\cdot g(1-1,1-1)\\
=& f(0,0)\cdot g(1,1)+f(0,1)\cdot g(1,0)\\
&+ f(1,0)\cdot g(0,1)+f(1,1)\cdot g(0,0)\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(1,2) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(1-i,2-j)\\
=& f(0,0)\cdot g(1-0,2-0)+f(0,1)\cdot g(1-0,2-1)+f(0,2)\cdot g(1-0,2-2)+f(0,3)\cdot g(1-0,2-3)\\
&+ f(1,0)\cdot g(1-1,2-0)+f(1,1)\cdot g(1-1,2-1)+f(1,2)\cdot g(1-1,2-2)+f(1,3)\cdot g(1-1,2-3)\\
&+ f(2,0)\cdot g(1-2,2-0)+f(2,1)\cdot g(1-2,2-1)+f(2,2)\cdot g(1-2,2-2)+f(2,3)\cdot g(1-2,2-3)\\
&+ f(3,0)\cdot g(1-3,2-0)+f(3,1)\cdot g(1-3,2-1)+f(3,2)\cdot g(1-3,2-2)+f(3,3)\cdot g(1-3,2-3)\\
=&f(0,1)\cdot g(1-0,2-1)+f(0,2)\cdot g(1-0,2-2)\\
&+f(1,1)\cdot g(1-1,2-1)+f(1,2)\cdot g(1-1,2-2)\\
=&f(0,1)\cdot g(1,1)+f(0,2)\cdot g(1,0)\\
&+f(1,1)\cdot g(0,1)+f(1,2)\cdot g(0,0)\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(1,3) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(1-i,3-j)\\
=& f(0,0)\cdot g(1-0,3-0)+f(0,1)\cdot g(1-0,3-1)+f(0,2)\cdot g(1-0,3-2)+f(0,3)\cdot g(1-0,3-3)\\
&+ f(1,0)\cdot g(1-1,3-0)+f(1,1)\cdot g(1-1,3-1)+f(1,2)\cdot g(1-1,3-2)+f(1,3)\cdot g(1-1,3-3)\\
&+ f(2,0)\cdot g(1-2,3-0)+f(2,1)\cdot g(1-2,3-1)+f(2,2)\cdot g(1-2,3-2)+f(2,3)\cdot g(1-2,3-3)\\
&+ f(3,0)\cdot g(1-3,3-0)+f(3,1)\cdot g(1-3,3-1)+f(3,2)\cdot g(1-3,3-2)+f(3,3)\cdot g(1-3,3-3)\\
=&f(0,2)\cdot g(1-0,3-2)+f(0,3)\cdot g(1-0,3-3)\\
&+f(1,2)\cdot g(1-1,3-2)+f(1,3)\cdot g(1-1,3-3)\\
=&f(0,2)\cdot g(1,1)+f(0,3)\cdot g(1,0)\\
&+f(1,2)\cdot g(0,1)+f(1,3)\cdot g(0,0)\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(1,4) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(1-i,4-j)\\
=& f(0,0)\cdot g(1-0,4-0)+f(0,1)\cdot g(1-0,4-1)+f(0,2)\cdot g(1-0,4-2)+f(0,3)\cdot g(1-0,4-3)\\
&+ f(1,0)\cdot g(1-1,4-0)+f(1,1)\cdot g(1-1,4-1)+f(1,2)\cdot g(1-1,4-2)+f(1,3)\cdot g(1-1,4-3)\\
&+ f(2,0)\cdot g(1-2,4-0)+f(2,1)\cdot g(1-2,4-1)+f(2,2)\cdot g(1-2,4-2)+f(2,3)\cdot g(1-2,4-3)\\
&+ f(3,0)\cdot g(1-3,4-0)+f(3,1)\cdot g(1-3,4-1)+f(3,2)\cdot g(1-3,4-2)+f(3,3)\cdot g(1-3,4-3)\\
=&f(0,3)\cdot g(1-0,4-3)\\
&+f(1,3)\cdot g(1-1,4-3)\\
=&f(0,3)\cdot g(1,1)\\
&+f(1,3)\cdot g(0,1)\\
=&0
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(2,0) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(2-i,0-j)\\
=& f(0,0)\cdot g(2-0,0-0)+f(0,1)\cdot g(2-0,0-1)+f(0,2)\cdot g(2-0,0-2)+f(0,3)\cdot g(2-0,0-3)\\
&+ f(1,0)\cdot g(2-1,0-0)+f(1,1)\cdot g(2-1,0-1)+f(1,2)\cdot g(2-1,0-2)+f(1,3)\cdot g(2-1,0-3)\\
&+ f(2,0)\cdot g(2-2,0-0)+f(2,1)\cdot g(2-2,0-1)+f(2,2)\cdot g(2-2,0-2)+f(2,3)\cdot g(2-2,0-3)\\
&+ f(3,0)\cdot g(2-3,0-0)+f(3,1)\cdot g(2-3,0-1)+f(3,2)\cdot g(2-3,0-2)+f(3,3)\cdot g(2-3,0-3)\\
=& f(1,0)\cdot g(2-1,0-0)\\
&+ f(2,0)\cdot g(2-2,0-0)\\
=& f(1,0)\cdot g(1,0)\\
&+ f(2,0)\cdot g(0,0)\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(2,1) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(2-i,1-j)\\
=& f(0,0)\cdot g(2-0,1-0)+f(0,1)\cdot g(2-0,1-1)+f(0,2)\cdot g(2-0,1-2)+f(0,3)\cdot g(2-0,1-3)\\
&+ f(1,0)\cdot g(2-1,1-0)+f(1,1)\cdot g(2-1,1-1)+f(1,2)\cdot g(2-1,1-2)+f(1,3)\cdot g(2-1,1-3)\\
&+ f(2,0)\cdot g(2-2,1-0)+f(2,1)\cdot g(2-2,1-1)+f(2,2)\cdot g(2-2,1-2)+f(2,3)\cdot g(2-2,1-3)\\
&+ f(3,0)\cdot g(2-3,1-0)+f(3,1)\cdot g(2-3,1-1)+f(3,2)\cdot g(2-3,1-2)+f(3,3)\cdot g(2-3,1-3)\\
=& f(1,0)\cdot g(2-1,1-0)+f(1,1)\cdot g(2-1,1-1)\\
&+ f(2,0)\cdot g(2-2,1-0)+f(2,1)\cdot g(2-2,1-1)\\
=& f(1,0)\cdot g(1,1)+f(1,1)\cdot g(1,0)\\
&+ f(2,0)\cdot g(0,1)+f(2,1)\cdot g(0,0)\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(2,2) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(2-i,2-j)\\
=& f(0,0)\cdot g(2-0,2-0)+f(0,1)\cdot g(2-0,2-1)+f(0,2)\cdot g(2-0,2-2)+f(0,3)\cdot g(2-0,2-3)\\
&+ f(1,0)\cdot g(2-1,2-0)+f(1,1)\cdot g(2-1,2-1)+f(1,2)\cdot g(2-1,2-2)+f(1,3)\cdot g(2-1,2-3)\\
&+ f(2,0)\cdot g(2-2,2-0)+f(2,1)\cdot g(2-2,2-1)+f(2,2)\cdot g(2-2,2-2)+f(2,3)\cdot g(2-2,2-3)\\
&+ f(3,0)\cdot g(2-3,2-0)+f(3,1)\cdot g(2-3,2-1)+f(3,2)\cdot g(2-3,2-2)+f(3,3)\cdot g(2-3,2-3)\\
=&f(1,1)\cdot g(2-1,2-1)+f(1,2)\cdot g(2-1,2-2)\\
&+f(2,1)\cdot g(2-2,2-1)+f(2,2)\cdot g(2-2,2-2)\\
=&f(1,1)\cdot g(1,1)+f(1,2)\cdot g(1,0)\\
&+f(2,1)\cdot g(0,1)+f(2,2)\cdot g(0,0)\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(2,3) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(2-i,3-j)\\
=& f(0,0)\cdot g(2-0,3-0)+f(0,1)\cdot g(2-0,3-1)+f(0,2)\cdot g(2-0,3-2)+f(0,3)\cdot g(2-0,3-3)\\
&+ f(1,0)\cdot g(2-1,3-0)+f(1,1)\cdot g(2-1,3-1)+f(1,2)\cdot g(2-1,3-2)+f(1,3)\cdot g(2-1,3-3)\\
&+ f(2,0)\cdot g(2-2,3-0)+f(2,1)\cdot g(2-2,3-1)+f(2,2)\cdot g(2-2,3-2)+f(2,3)\cdot g(2-2,3-3)\\
&+ f(3,0)\cdot g(2-3,3-0)+f(3,1)\cdot g(2-3,3-1)+f(3,2)\cdot g(2-3,3-2)+f(3,3)\cdot g(2-3,3-3)\\
=& f(1,2)\cdot g(2-1,3-2)+f(1,3)\cdot g(2-1,3-3)\\
&+f(2,2)\cdot g(2-2,3-2)+f(2,3)\cdot g(2-2,3-3)\\
=& f(1,2)\cdot g(1,1)+f(1,3)\cdot g(1,0)\\
&+f(2,2)\cdot g(0,1)+f(2,3)\cdot g(0,0)\\
=& -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(2,4) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(2-i,4-j)\\
=& f(0,0)\cdot g(2-0,4-0)+f(0,1)\cdot g(2-0,4-1)+f(0,2)\cdot g(2-0,4-2)+f(0,3)\cdot g(2-0,4-3)\\
&+ f(1,0)\cdot g(2-1,4-0)+f(1,1)\cdot g(2-1,4-1)+f(1,2)\cdot g(2-1,4-2)+f(1,3)\cdot g(2-1,4-3)\\
&+ f(2,0)\cdot g(2-2,4-0)+f(2,1)\cdot g(2-2,4-1)+f(2,2)\cdot g(2-2,4-2)+f(2,3)\cdot g(2-2,4-3)\\
&+ f(3,0)\cdot g(2-3,4-0)+f(3,1)\cdot g(2-3,4-1)+f(3,2)\cdot g(2-3,4-2)+f(3,3)\cdot g(2-3,4-3)\\
=& f(1,3)\cdot g(2-1,4-3)\\
&+f(2,3)\cdot g(2-2,4-3)\\
=& f(1,3)\cdot g(1,1)\\
&+f(2,3)\cdot g(0,1)\\
=& -4
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(3,0) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(3-i,0-j)\\
=& f(0,0)\cdot g(3-0,0-0)+f(0,1)\cdot g(3-0,0-1)+f(0,2)\cdot g(3-0,0-2)+f(0,3)\cdot g(3-0,0-3)\\
&+ f(1,0)\cdot g(3-1,0-0)+f(1,1)\cdot g(3-1,0-1)+f(1,2)\cdot g(3-1,0-2)+f(1,3)\cdot g(3-1,0-3)\\
&+ f(2,0)\cdot g(3-2,0-0)+f(2,1)\cdot g(3-2,0-1)+f(2,2)\cdot g(3-2,0-2)+f(2,3)\cdot g(3-2,0-3)\\
&+ f(3,0)\cdot g(3-3,0-0)+f(3,1)\cdot g(3-3,0-1)+f(3,2)\cdot g(3-3,0-2)+f(3,3)\cdot g(3-3,0-3)\\
=& f(2,0)\cdot g(3-2,0-0)\\
& + f(3,0)\cdot g(3-3,0-0)\\
=& f(2,0)\cdot g(1,0)\\
& + f(3,0)\cdot g(0,0)\\
= & -3
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(3,1) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(3-i,1-j)\\
=& f(0,0)\cdot g(3-0,1-0)+f(0,1)\cdot g(3-0,1-1)+f(0,2)\cdot g(3-0,1-2)+f(0,3)\cdot g(3-0,1-3)\\
&+ f(1,0)\cdot g(3-1,1-0)+f(1,1)\cdot g(3-1,1-1)+f(1,2)\cdot g(3-1,1-2)+f(1,3)\cdot g(3-1,1-3)\\
&+ f(2,0)\cdot g(3-2,1-0)+f(2,1)\cdot g(3-2,1-1)+f(2,2)\cdot g(3-2,1-2)+f(2,3)\cdot g(3-2,1-3)\\
&+ f(3,0)\cdot g(3-3,1-0)+f(3,1)\cdot g(3-3,1-1)+f(3,2)\cdot g(3-3,1-2)+f(3,3)\cdot g(3-3,1-3)\\
= & f(2,0)\cdot g(3-2,1-0)+f(2,1)\cdot g(3-2,1-1)\\
& + f(3,0)\cdot g(3-3,1-0)+f(3,1)\cdot g(3-3,1-1)\\
= & f(2,0)\cdot g(1,1)+f(2,1)\cdot g(1,0)\\
& + f(3,0)\cdot g(0,1)+f(3,1)\cdot g(0,0)\\
= & -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(3,2) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(3-i,2-j)\\
=& f(0,0)\cdot g(3-0,2-0)+f(0,1)\cdot g(3-0,2-1)+f(0,2)\cdot g(3-0,2-2)+f(0,3)\cdot g(3-0,2-3)\\
&+ f(1,0)\cdot g(3-1,2-0)+f(1,1)\cdot g(3-1,2-1)+f(1,2)\cdot g(3-1,2-2)+f(1,3)\cdot g(3-1,2-3)\\
&+ f(2,0)\cdot g(3-2,2-0)+f(2,1)\cdot g(3-2,2-1)+f(2,2)\cdot g(3-2,2-2)+f(2,3)\cdot g(3-2,2-3)\\
&+ f(3,0)\cdot g(3-3,2-0)+f(3,1)\cdot g(3-3,2-1)+f(3,2)\cdot g(3-3,2-2)+f(3,3)\cdot g(3-3,2-3)\\
=& f(2,1)\cdot g(3-2,2-1)+f(2,2)\cdot g(3-2,2-2)\\
& +f(3,1)\cdot g(3-3,2-1)+f(3,2)\cdot g(3-3,2-2)\\
=& f(2,1)\cdot g(1,1)+f(2,2)\cdot g(1,0)\\
& +f(3,1)\cdot g(0,1)+f(3,2)\cdot g(0,0)\\
= & -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(3,3) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(3-i,3-j)\\
=& f(0,0)\cdot g(3-0,3-0)+f(0,1)\cdot g(3-0,3-1)+f(0,2)\cdot g(3-0,3-2)+f(0,3)\cdot g(3-0,3-3)\\
&+ f(1,0)\cdot g(3-1,3-0)+f(1,1)\cdot g(3-1,3-1)+f(1,2)\cdot g(3-1,3-2)+f(1,3)\cdot g(3-1,3-3)\\
&+ f(2,0)\cdot g(3-2,3-0)+f(2,1)\cdot g(3-2,3-1)+f(2,2)\cdot g(3-2,3-2)+f(2,3)\cdot g(3-2,3-3)\\
&+ f(3,0)\cdot g(3-3,3-0)+f(3,1)\cdot g(3-3,3-1)+f(3,2)\cdot g(3-3,3-2)+f(3,3)\cdot g(3-3,3-3)\\
= & f(2,2)\cdot g(3-2,3-2)+f(2,3)\cdot g(3-2,3-3)\\
&+f(3,2)\cdot g(3-3,3-2)+f(3,3)\cdot g(3-3,3-3)\\
= & f(2,2)\cdot g(1,1)+f(2,3)\cdot g(1,0)\\
&+f(3,2)\cdot g(0,1)+f(3,3)\cdot g(0,0)\\
= & -7
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(3,4) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(3-i,4-j)\\
=& f(0,0)\cdot g(3-0,4-0)+f(0,1)\cdot g(3-0,4-1)+f(0,2)\cdot g(3-0,4-2)+f(0,3)\cdot g(3-0,4-3)\\
&+ f(1,0)\cdot g(3-1,4-0)+f(1,1)\cdot g(3-1,4-1)+f(1,2)\cdot g(3-1,4-2)+f(1,3)\cdot g(3-1,4-3)\\
&+ f(2,0)\cdot g(3-2,4-0)+f(2,1)\cdot g(3-2,4-1)+f(2,2)\cdot g(3-2,4-2)+f(2,3)\cdot g(3-2,4-3)\\
&+ f(3,0)\cdot g(3-3,4-0)+f(3,1)\cdot g(3-3,4-1)+f(3,2)\cdot g(3-3,4-2)+f(3,3)\cdot g(3-3,4-3)\\
= & f(2,3)\cdot g(3-2,4-3)\\
& +f(3,3)\cdot g(3-3,4-3)\\
= & f(2,3)\cdot g(1,1)\\
& +f(3,3)\cdot g(0,1)\\
= & -8
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(4,0) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(4-i,0-j)\\
=& f(0,0)\cdot g(4-0,0-0)+f(0,1)\cdot g(4-0,0-1)+f(0,2)\cdot g(4-0,0-2)+f(0,3)\cdot g(4-0,0-3)\\
&+ f(1,0)\cdot g(4-1,0-0)+f(1,1)\cdot g(4-1,0-1)+f(1,2)\cdot g(4-1,0-2)+f(1,3)\cdot g(4-1,0-3)\\
&+ f(2,0)\cdot g(4-2,0-0)+f(2,1)\cdot g(4-2,0-1)+f(2,2)\cdot g(4-2,0-2)+f(2,3)\cdot g(4-2,0-3)\\
&+ f(3,0)\cdot g(4-3,0-0)+f(3,1)\cdot g(4-3,0-1)+f(3,2)\cdot g(4-3,0-2)+f(3,3)\cdot g(4-3,0-3)\\
=&f(3,0)\cdot g(4-3,0-0)\\
=&f(3,0)\cdot g(1,0)\\
= & 52
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(4,1) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(4-i,1-j)\\
=& f(0,0)\cdot g(4-0,1-0)+f(0,1)\cdot g(4-0,1-1)+f(0,2)\cdot g(4-0,1-2)+f(0,3)\cdot g(4-0,1-3)\\
&+ f(1,0)\cdot g(4-1,1-0)+f(1,1)\cdot g(4-1,1-1)+f(1,2)\cdot g(4-1,1-2)+f(1,3)\cdot g(4-1,1-3)\\
&+ f(2,0)\cdot g(4-2,1-0)+f(2,1)\cdot g(4-2,1-1)+f(2,2)\cdot g(4-2,1-2)+f(2,3)\cdot g(4-2,1-3)\\
&+ f(3,0)\cdot g(4-3,1-0)+f(3,1)\cdot g(4-3,1-1)+f(3,2)\cdot g(4-3,1-2)+f(3,3)\cdot g(4-3,1-3)\\
= & f(3,0)\cdot g(4-3,1-0)+f(3,1)\cdot g(4-3,1-1)\\
= & f(3,0)\cdot g(1,1)+f(3,1)\cdot g(1,0)\\
= & 30
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(4,2) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(4-i,2-j)\\
=& f(0,0)\cdot g(4-0,2-0)+f(0,1)\cdot g(4-0,2-1)+f(0,2)\cdot g(4-0,2-2)+f(0,3)\cdot g(4-0,2-3)\\
&+ f(1,0)\cdot g(4-1,2-0)+f(1,1)\cdot g(4-1,2-1)+f(1,2)\cdot g(4-1,2-2)+f(1,3)\cdot g(4-1,2-3)\\
&+ f(2,0)\cdot g(4-2,2-0)+f(2,1)\cdot g(4-2,2-1)+f(2,2)\cdot g(4-2,2-2)+f(2,3)\cdot g(4-2,2-3)\\
&+ f(3,0)\cdot g(4-3,2-0)+f(3,1)\cdot g(4-3,2-1)+f(3,2)\cdot g(4-3,2-2)+f(3,3)\cdot g(4-3,2-3)\\
= & f(3,1)\cdot g(4-3,2-1)+f(3,2)\cdot g(4-3,2-2)\\
= & f(3,1)\cdot g(1,1)+f(3,2)\cdot g(1,0)\\
= & 32
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(4,3) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(4-i,3-j)\\
=& f(0,0)\cdot g(4-0,3-0)+f(0,1)\cdot g(4-0,3-1)+f(0,2)\cdot g(4-0,3-2)+f(0,3)\cdot g(4-0,3-3)\\
&+ f(1,0)\cdot g(4-1,3-0)+f(1,1)\cdot g(4-1,3-1)+f(1,2)\cdot g(4-1,3-2)+f(1,3)\cdot g(4-1,3-3)\\
&+ f(2,0)\cdot g(4-2,3-0)+f(2,1)\cdot g(4-2,3-1)+f(2,2)\cdot g(4-2,3-2)+f(2,3)\cdot g(4-2,3-3)\\
&+ f(3,0)\cdot g(4-3,3-0)+f(3,1)\cdot g(4-3,3-1)+f(3,2)\cdot g(4-3,3-2)+f(3,3)\cdot g(4-3,3-3)\\
= & f(3,2)\cdot g(4-3,3-2)+f(3,3)\cdot g(4-3,3-3)\\
= & f(3,2)\cdot g(1,1)+f(3,3)\cdot g(1,0)\\
= & 34
\end{array}
\]
\[\begin{array}{ll}
&(f*g)(4,4) \\
=&\sum_{i=0}^{3}\sum_{j=0}^{3}f(i,j)\cdot g(4-i,4-j)\\
=& f(0,0)\cdot g(4-0,4-0)+f(0,1)\cdot g(4-0,4-1)+f(0,2)\cdot g(4-0,4-2)+f(0,3)\cdot g(4-0,4-3)\\
&+ f(1,0)\cdot g(4-1,4-0)+f(1,1)\cdot g(4-1,4-1)+f(1,2)\cdot g(4-1,4-2)+f(1,3)\cdot g(4-1,4-3)\\
&+ f(2,0)\cdot g(4-2,4-0)+f(2,1)\cdot g(4-2,4-1)+f(2,2)\cdot g(4-2,4-2)+f(2,3)\cdot g(4-2,4-3)\\
&+ f(3,0)\cdot g(4-3,4-0)+f(3,1)\cdot g(4-3,4-1)+f(3,2)\cdot g(4-3,4-2)+f(3,3)\cdot g(4-3,4-3)\\
= & f(3,3)\cdot g(4-3,4-3)\\
= & f(3,3)\cdot g(1,1)\\
= & -32
\end{array}
\]
从上面的计算机过程,我们可以得到一个计算规则(考虑由于不在f的支撑集上而抵消掉的g的相关项)
在上面的公式中观察可以看到
\[\begin{array}{l}
?\cdot g(1,1)+?\cdot g(1,0)+\\
?\cdot g(0,1)+?\cdot g(0,0)\\
\end{array}
\]
即,始终有f中元素与一个如下的矩阵的Hadamard乘积
\[\left[
\begin{array}{ll}
g(1,1) & g(1,0)\\
g(0,1) & g(0,0)\\
\end{array}
\right]
\]
而上面矩阵实际上就是g矩阵的180度翻转.
通过数学归纳法,容易得到更加一般化的结论.
方法二 (程序实现更便捷,卷积的数学直观性没有方法一好)
先将 g 进行180度翻转,具体为先左右翻转,然后再上下翻转,得到
\[g=\left[\begin{array}{rr}
-3 & 1 \\
4 & -2
\end{array}\right]\overset{Left\, and\, Right}{=}
\left[\begin{array}{rr}
1 & -3 \\
-2 & 4
\end{array}\right]\overset{Top\, and\, Bottom}{=}
\left[\begin{array}{rr}
-2 & 4 \\
1 & -3
\end{array}\right]=
g_{180}
\]
然后用\(g_{180}\)去横扫\(f\).
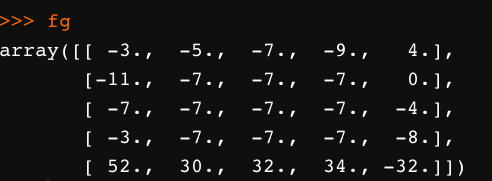
Python 简单计算如下
import numpy as np
from scipy import signal
f = (np.arange(16).reshape((4,4))+1)
g = np.array([[-3,1],[4,-2]],np.float32)
fg = signal.convolve2d(f,g,mode="full")
计算结果为



 浙公网安备 33010602011771号
浙公网安备 33010602011771号