5 决策树

决策树

---

 

决策树（decision tree）是一种基本的分类与回归方法。本章主要讨论用于分类的决策树。

 

决策树模型与学习

---

 决策树模型 

决策树由结点（node）和有向边（directed edge）组成。结点有两种类型：内部结点（internalnode）和叶结点（leaf node）。内部结点表示一个特征或属性，叶结点表示一个类。

用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点，接着向下重复上述过程，直到到达叶节点，将实例分到叶节点对应的类中。

 

 

 

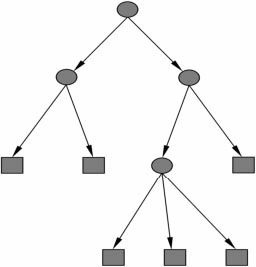
决策树与if-then规则 

决策树的路径或其对应的if-then规则集合具有一个重要的性质：互斥并且完备。这就是说，每一个实例都只能被一条路径或一条规则所覆盖。

决策树与条件概率分布

决策树还表示给定特征条件下类的条件概率分布。这一条件概率分布定义在特征空间的一个划分（partition）上。

给定实例的特征X，一定落入某个划分，决策树选取该划分里最大概率的类作为结果输出。

当某个单元c的条件概率满足P(Y＝+1|X＝c)>0.5时，则认为这个单元属于正类，即落在这个单元的实例都被视为正例。

如图：

 

                        

 

决策树学习

决策树学习的目标是根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。决策树学习的损失函数通常是正则化的极大似然函数。决策树学习的策略是以损失函数为目标函数的最小化。 

决策树学习算法包含特征选择、决策树的生成与剪枝过程。决策树的学习算法一般是递归地选择最优特征，并用最优特征对数据集进行分割。开始时，构建根节点，选择最优特征，该特征有几种值就分割为几个子集，每个子集分别递归调用此方法，返回节点，返回的节点就是上一层的子节点。直到数据集为空，或者数据集只有一维特征为止。由于可能发生过拟合现象，需要对已生成的树自下而上进行剪枝，将树变得更简单，从而使它具有更好的泛化能力。

由于决策树表示一个条件概率分布，所以深浅不同的决策树对应着不同复杂度的概率模型。决策树的生成对应于模型的局部选择（训练集），决策树的剪枝对应于模型的全局选择。决策树的生成只考虑局部最优，相对地，决策树的剪枝则考虑全局最优。 

 

特征选择

---

 

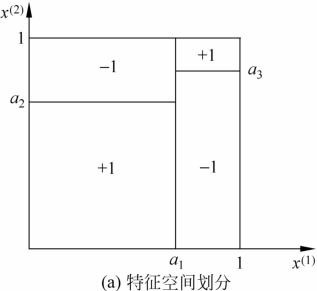
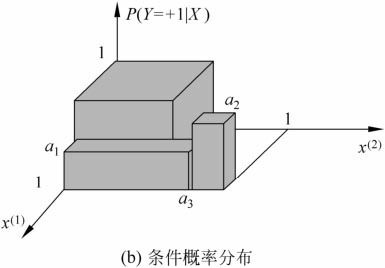
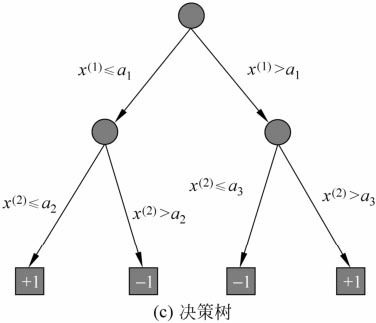
特征选择在于选取对训练数据具有分类能力的特征。通常特征选择的准则是信息增益或信息增益比。

信息增益

熵（entropy）是表示随机变量不确定性的度量。设X是一个取有限个值的离散随机变量，其概率分布为 P（X=x_i）= p_i，则随机变量X的熵定义为：

熵越大，随机变量的不确定性就越大。从定义可验证 0 ≤ H（P）≤ logn

条件熵 H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性，定义为X给定条件下Y的条件概 率分布的熵对X的数学期望：

当熵和条件熵中的概率由数据估计（特别是极大似然估计）得到时，所对应的熵与条 件熵分别称为经验熵（empirical entropy）和经验条件熵（empirical conditional entropy）。

信息增益（information gain）表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。其定义如下：特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即： g（D,A）= H(D)- H(D|A)

一般地，熵 H(Y)与条件熵 H(Y|X)之差称为互信息（mutual information）。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。

信息增益比

信息增益值的大小是相对于训练数据集而言的，并没有绝对意义。在分类问题困难时，也就是说在训练数据集的经验熵大的时候，信息增益值会偏大。反之，信息增益值会偏小。使用信息增益比（information gain ratio）可以对这一问题进行校正。信息增益比g_R(D,A)定义为其信息增益g(D,A)与训练数据集D的经验熵H(D)之比：

决策树的生成

---

ID3算法 

ID3算法的核心是在决策树各个结点上用信息增益准则选择特征，递归地构建决策树。ID3相当于用极大似然法进行概率模型的选择。

ID3算法只有树的生成，所以该算法生成的树容易产生过拟合。

C4.5的生成算法

C4.5在生成的过程中，用信息增益比来选择特征。

 

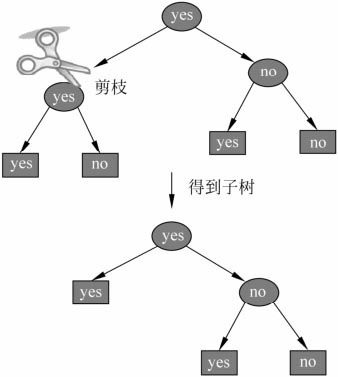
决策树的剪枝

---

 

 

决策树的剪枝往往通过极小化决策树整体的损失函数（loss function）或代价函数 （cost function）来实现。

设树T的叶结点个数为T，t是树T的叶结点，叶结点有N_t个样本点，其中k类的样本点有N_tk个，H_t(T)为叶结点t上的经验熵，a≥0为参数，则决策树学习的损失函数可以定义为：

 

在损失函数中，将右端的第1项记作：

这时有：

C(T)表示模型对训练数据的预测误差，即模型与训练数据的拟合程度，|T|表示模型复杂度，参数a≥0控制两者之间的影响。较大的a促使选择较简单的模型（树），较小的a促使选择较复杂的模型（树）。（因为当a较大时，如果模型复杂度|T|很大，右边第二项相对于第一项而言会非常大，最终的损失函数达不到极小值，要想使损失函数达到极小值，那么第二项应该较小，而a较大，只能模型复杂度|T|较小才可以·）a＝0意味着只考虑模型与训练数据的拟合程度，不考虑模型的复杂度。 

剪枝，就是当a确定时，选择损失函数最小的模型，即损失函数最小的子树。

上面定义的损失函数的极小化等价于正则化的极大似然估计。所以，利用损失函数最小原则进行剪枝就是用正则化的极大似然估计进行模型选择。 

剪枝算法：

从每个叶节点往上走，走了后如果损失函数减小了，则减掉叶节点，将父节点作为叶节点。

 

 

由于只需考虑两个树的损失函数的差，其计算可以在局部进行。所以，决策树的剪枝算法可以由一种动态规划的算法实现。

 

CART算法

---

 

CART同样由特征选择、树的生成及剪枝组成， 既可以用于分类也可以用于回归。以下将用于分类与回归的树统称为决策树。

 

CART生成

决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数（Gini index）最小化准则，进行特征选择，生成二叉树。

回归树的生成

选择第j个变量x^（j）和它的取值s，作为切分变量（splitting variable）和切分点（splitting point），并定义两个区域：

 

 

 

 

用平方误差最小的准则求解每个单元上的最优输出值。易知，单元R_m上的c_m的最优值是R_m上的所有输入实例x_i对应的输出y_i的均值（假设一个区域中有两组数据，y₁=0，y₂=a，相当于平方误差 y = x²+（a-x）²，通过求导易得x为 a/2，也就是均值），即

 

 

通过寻找最小均方误差点，实现切分：

 

 

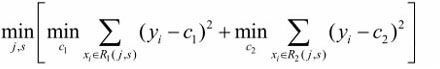
遍历所有输入变量，找到最优的切分变量j，构成一个对(j,s)。依此将输入空间划分为两个区域。接着，对每个区域重复上述划分过程，直到满足停止条件为止。这样就生成一棵回归树。这样的回归树通常称为最小二乘回归树（least squares regression tree）。（其实就是一种暴力解法）

 

分类树的生成

分类树用基尼指数选择最优特征，同时决定该特征的最优二值切分点。

基尼指数：分类问题中，假设有K个类，样本点属于第k类的概率为p_k，则概率分布的基尼指数定义为：

 

 

 

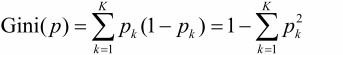
对于二类分类问题，若样本点属于第1个类的概率是p，则概率分布的基尼指数为 Gini(p) = 2p(1-p)

如果样本集合D根据特征A是否取某一可能值a被分割成D₁和D₂两部分,则在特征A的条件下，集合D的基尼指数定义为

 

 

基尼指数值越大，样本集合的不确定性也就越大，这一点与熵相似。 

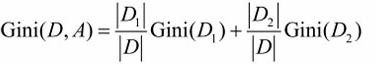
下图显示二类分类问题中基尼指数Gini(p)、熵之半 0.5H(p)和分类误差率的关系。横坐标表示概率p，纵坐标表示损失。可以看出基尼指数和熵之半的曲线很接近，都可以近似地代表分类差率。

 

 

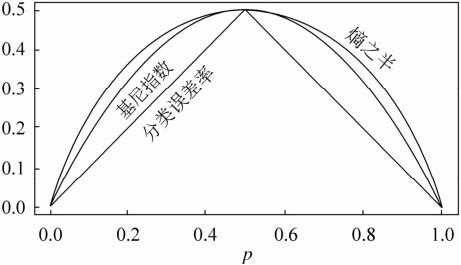
回归树用平方误差选择最优特征，分类树用基尼指数选择最优特征，除此之外基本流程基本相同。

 

CART剪枝 

CART剪枝算法从“完全生长”的决策树的底端剪去一些子树，使决策树变小（模型变简单），从而能够对未知数据有更准确的预测。

对固定的a，一定存在使损失函数C_a(T)最小的子树，将其表示为T_a。T_a在损失函数C_a(T)最小的意义下是最优的。容易验证这样的最优子树是唯一的。当a大的时候，最优子树T_a偏小；当a小的时候，最优子树T_a偏大。极端情况，当a＝0时，整体树是最优的。当a→ ∞时，根结点组成的单结点树是最优的。设对a递增的序列，对应的最优子树序列为T_n，子树序列第一棵包含第二棵，依次类推。

具体地，从整体树T₀开始剪枝。对T₀的任意内部结点t，以t为单结点树的损失函数是 C_a（t）= C（t）+ a

以t为根结点的子树T_t的损失函数是 C_a（T_t）= C（T_t）+ a|T_t|

当a＝0及a充分小时（整体树最优），有不等式 C_a（T_t）< C_a（t）

当a增大到∞时，这个不等式的符号会反过来,由零点定理可以得出，至少存在一点a，使得 C_a（T_t）= C_a（t），此时 ，

T_t与t有相同的损失函数值，而t的结点少，因此t比T_t更可取，对T_t进行剪枝。 为此，对T₀中每一内部结点t，计算     ，它表示剪枝后整体损失函数减少的程度，即a。

在T₀中剪去g(t)最小的T_t，将得到的子树作为T₁，同时将最小的g(t)设为a₁。T1为区间[a₁,a₂)的最优子树。如此剪枝下去，直至得到根结点。在这一过程中，不断地增加a的值，产生新的区间。

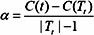对此子树序列，应用独立的验证数据集交叉验证，平方误差或基尼指数最小的决策树被认为是最优的决策树，在子树序列中，每棵子树T₁,T₂,…,T_n都对应于一个参数a₁,a₂,…,a_n，所以，当最优子树T_k确定时，对应的a_k也确定了，即得到最优决策树T_a。