大顶堆的构建与排序

大顶堆

有一类常见的面试问题：如何从一个存有10亿个数字的文档中获取到最大的10个数，计算机内存只有1M？

---

实际上这种问题可以使用大顶堆的数据结构来解答，让我们来看一下大顶堆的构建和排序过程

1. 什么是堆

堆是一种非线性结构，可以把堆看作一棵二叉树，也可以看作一个数组，即：堆就是利用完全二叉树的结构来维护的一维数组。

堆可以分为大顶堆和小顶堆。
大顶堆：每个结点的值都大于或等于其左右孩子结点的值。
小顶堆：每个结点的值都小于或等于其左右孩子结点的值。

如果是排序，求升序用大顶堆，求降序用小顶堆。
一般我们说 topK 问题，就可以用大顶堆或小顶堆来实现，
最大的 K 个：小顶堆
最小的 K 个：大顶堆

2、大顶堆的构建过程

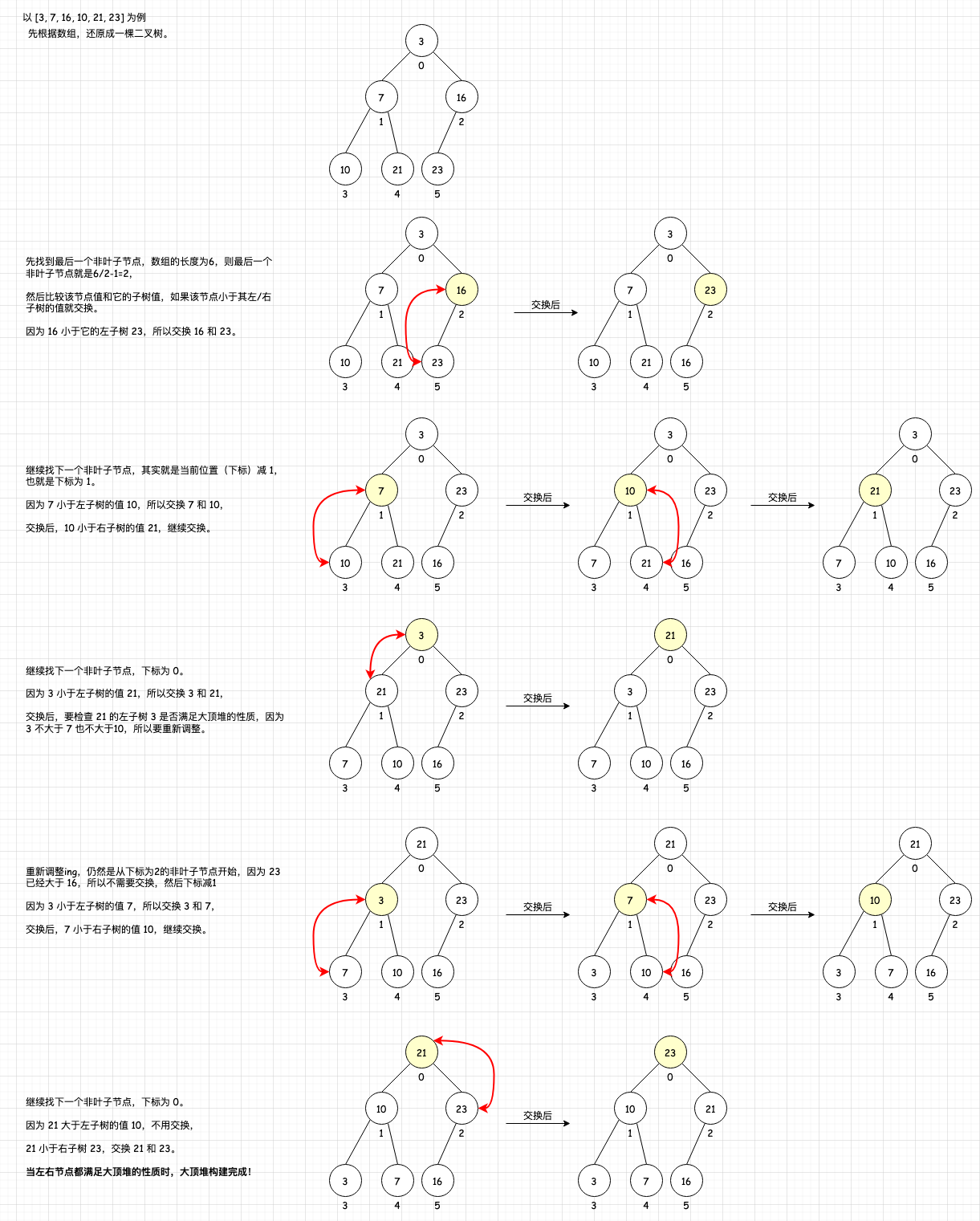
大顶堆的构建过程就是从最后一个非叶子结点开始从下往上调整。

最后一个非叶子节点怎么找？这里我们用数组表示待排序序列，则最后一个非叶子结点的位置是：数组长度/2-1。假如数组长度为9，则最后一个非叶子结点位置是 9/2-1=3。

比较当前结点的值和左子树的值，如果当前节点小于左子树的值，就交换当前节点和左子树；

交换完后要检查左子树是否满足大顶堆的性质，不满足则重新调整子树结构；
再比较当前结点的值和右子树的值，如果当前节点小于右子树的值，就交换当前节点和右子树；

交换完后要检查右子树是否满足大顶堆的性质，不满足则重新调整子树结构；
无需交换调整的时候，则大顶堆构建完成。
画个图理解下，以 [3, 7, 16, 10, 21, 23] 为例：

public class BuildBigHeap {

    /**
     * 构建大顶堆
     * 大顶堆的性质：每个结点的值都大于或等于其左右子结点的值。
     */
    public void buildBigHeap(int[] arr) {
        int len = arr.length;

        for (int i = (int) (Math.floor(len / 2) - 1); i >= 0; i--) {
            // 根节点小于左子树
            if (2 * i + 1 < len && arr[2 * i + 1] > arr[i]) {
                swap(arr, i, 2 * i + 1);

                //检查左子树是否满足大顶堆的性质，如果不满足，则重新调整
                if (( 2 * (2 * i + 1) + 1 < len && arr[2 * i + 1] < arr[2 * (2 * i + 1) + 1])
                        || ( 2 * (2 * i + 1) + 2 < len && arr[2 * i + 1] < arr[2 * (2 * i + 1) + 2] )) {
                    buildBigHeap(arr);
                }
            }

            // 根节点小于右子树
            if (2 * i + 2 < len && arr[i] < arr[2 * i + 2]) {
                //交换根节点和右子树的值
                swap(arr, i, 2 * i + 2);
                // $temp = $arr[$i];
                // $arr[$i] = $arr[2 * $i + 2];
                // $arr[2 * $i + 2] = $temp;
                //检查右子树是否满足大顶堆的性质，如果不满足，则重新调整
                if ((2 * (2 * i + 2) + 1 < len && arr[2 * i + 2] < arr[2 * (2 * i + 2) + 1])
                        || (2 * (2 * i + 2) + 2 < len && arr[2 * i + 2] < arr[2 * (2 * i + 2) + 2])) {
                    buildBigHeap(arr);
                }
            }


        }
    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

3、大顶堆的排序过程

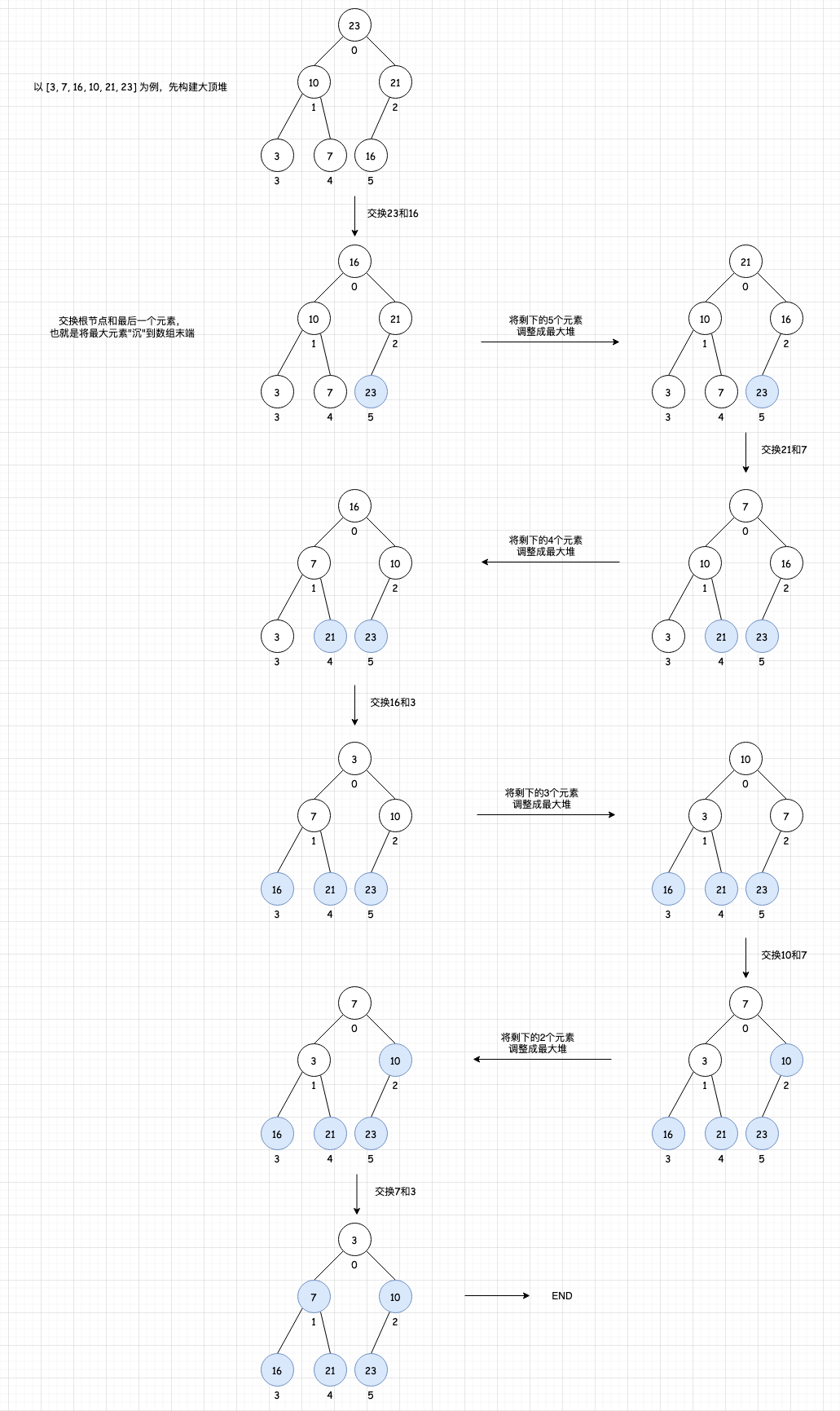
将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值，如此反复执行，便能得到一个有序序列了。

是不是对上面这一大段文字很头疼？其实排序过程用下面 4 步就能概括：
第 1 步：先 n 个元素的无序序列，构建成大顶堆
第 2 步：将根节点与最后一个元素交换位置，（将最大元素"沉"到数组末端）
第 3 步：交换过后可能不再满足大顶堆的条件，所以需要将剩下的 n-1 个元素重新构建成大顶堆
第 4 步：重复第 2 步、第 3 步直到整个数组排序完成。

/**
 * 交换交换根节点和数组末尾元素的值
 */
public void adjustHeap(int[] heap) {
    int len = heap.length;

    int temp = heap[0];
    heap[0] = heap[len - 1];
    heap[len - 1] = temp;

}

/**
 * 堆排序
 */
public void heapSort(int[] arr) {
    int len = arr.length;
   
    for (int i = len; i > 0; i--) {
        //重新构建大顶堆
        buildBigHeap(arr);
        //交换根节点和数组末尾元素的值
        adjustHeap(arr);
    }
}

---

在说回到我们前面提到的面试提。考虑10亿个数据很多，一次性无法装到我们的计算内存中， 采用常用的排序算法，可能也是不好进行操作，数据量很大， 这个地方可以想到可以才用小顶堆来解决这个问题。

1、让计算机去io读取文件
2、把读取出来的数据去构建一个包含10个元素的小顶堆
3、构建完成后，每次从文件中读取出来的一个数字和堆顶的元素进行比较， 如果比堆顶元素小，就直接丢弃或者跳过。如果读取出来的数据比堆顶元素大， 那么就可以用这个元素替代堆顶元素，进行调整小顶堆