实验一:
#include <stdio.h> #define N 4 #define M 2 void test1() { int x[N] = {1, 9, 8, 4}; int i; // 输出数组x占用的内存字节数 printf("sizeof(x) = %d\n", sizeof(x)); // 输出每个元素的地址、值 for (i = 0; i < N; ++i) printf("%p: %d\n", &x[i], x[i]); // 输出数组名x对应的值 printf("x = %p\n", x); } void test2() { int x[M][N] = {{1, 9, 8, 4}, {2, 0, 4, 9}}; int i, j; // 输出二维数组x占用的内存字节数 printf("sizeof(x) = %d\n", sizeof(x)); // 输出每个元素的地址、值 for (i = 0; i < M; ++i) for (j = 0; j < N; ++j) printf("%p: %d\n", &x[i][j], x[i][j]); printf("\n"); // 输出二维数组名x, 以及,x[0], x[1]的值 printf("x = %p\n", x); printf("x[0] = %p\n", x[0]); printf("x[1] = %p\n", x[1]); printf("\n"); } int main() { printf("测试1: int型一维数组\n"); test1(); printf("\n测试2: int型二维数组\n"); test2(); return 0; }
实验结果:
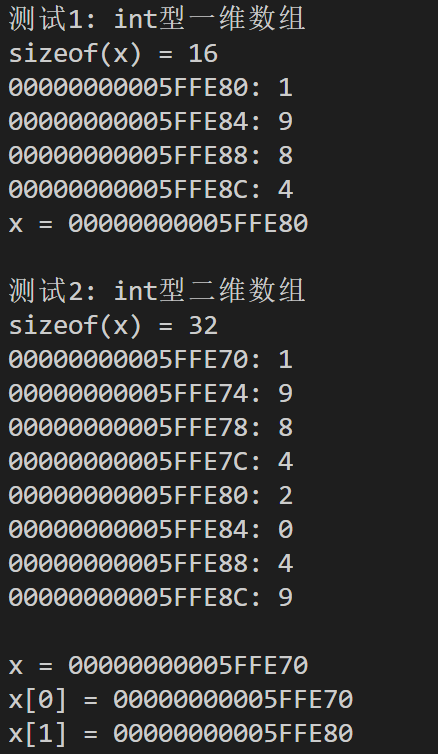
问题一:
一维数组连续存放,x与&x[0]值相同
问题二:
二维数组连续存放,x,x[0]和&x[0][0]相同。x[0]和x[1]相差4,该差值为该数组所存储数据类型所占字节数
实验二:
#include <stdio.h> #define N 100 // 函数声明 void input(int x[], int n); double compute(int x[], int n); int main() { int x[N]; int n, i; double ans; while (printf("Enter n: "), scanf("%d", &n) != EOF) { input(x, n); // 函数调用 ans = compute(x, n); // 函数调用 printf("ans = %.2f\n\n", ans); } return 0; } // 函数定义 void input(int x[], int n) { int i; for (i = 0; i < n; ++i) scanf("%d", &x[i]); } // 函数定义 double compute(int x[], int n) { int i, high, low; double ans; high = low = x[0]; ans = 0; for (i = 0; i < n; ++i) { ans += x[i]; if (x[i] > high) high = x[i]; else if (x[i] < low) low = x[i]; } ans = (ans - high - low) / (n - 2); return ans; }
实验结果:
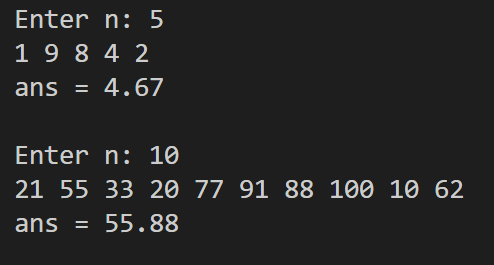
问题一:
形参形式:x[]
实参形式:x
问题二:
input:用于传入数组的大小,输入数组的值
compute:去掉数组中的最大值和最小值,求平均
任务三:
#include <stdio.h> #define N 100 // 函数声明 void output(int x[][N], int n); void init(int x[][N], int n, int value); int main() { int x[N][N]; int n, value; while (printf("Enter n and value: "), scanf("%d%d", &n, &value) != EOF) { init(x, n, value); // 函数调用 output(x, n); // 函数调用 printf("\n"); } return 0; } // 函数定义 void output(int x[][N], int n) { int i, j; for (i = 0; i < n; ++i) { for (j = 0; j < n; ++j) printf("%d ", x[i][j]); printf("\n"); } } // 函数定义 void init(int x[][N], int n, int value) { int i, j; for (i = 0; i < n; ++i) for (j = 0; j < n; ++j) x[i][j] = value; }
实验结果:
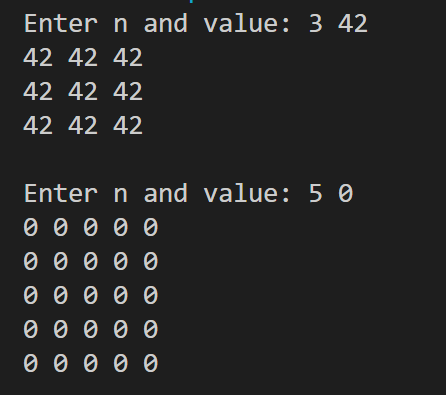
问题一:
形参:x[][N]
实参:x
问题二:
不能,计算地址偏移量的时候需要用到第二维的大小
问题三:
output:输出数组元素
init:按照输入的行列数和值,生成一个数组
任务四:
#include <stdio.h> #define N 100 // 函数声明 // 待补足 void input(int x[], int n); double median(int x[], int n); int main() { int x[N]; int n; double ans; while (printf("Enter n: "), scanf("%d", &n) != EOF) { input(x, n); // 函数调用 ans = median(x, n); // 函数调用 printf("ans = %g\n\n", ans); } return 0; } void input(int x[], int n) { for (int i = 0; i < n; i++) { scanf("%d", &x[i]); } } double median(int x[], int n) { for (int i = 0; i < n - 1; i++) { for (int j = 0; j < n - i - 1; j++) { if (x[j] > x[j+1]) { int temp = x[j]; x[j] = x[j + 1]; x[j + 1] = temp; } } } if (n % 2 == 0) { return (x[n / 2 - 1] + x[n / 2]) / 2.0; } else { return x[n / 2]*1.0; } }
实验结果:
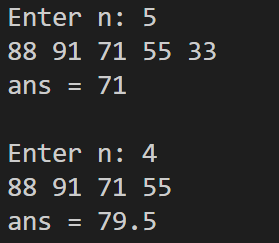
任务五:
#include <stdio.h> #define N 100 // 函数声明 void input(int x[][N], int n); void output(int x[][N], int n); // 函数rotate_to_right声明 // 待补足 void rotate_to_right(int x[][N], int n); int main() { int x[N][N]; int n; printf("Enter n: "); scanf("%d", &n); input(x, n); printf("原始矩阵:\n"); output(x, n); // 函数rotate_to_right调用 rotate_to_right(x, n); printf("变换后矩阵:\n"); output(x, n); return 0; } // 函数定义 // 功能: 输入一个n*n的矩阵x void input(int x[][N], int n) { int i, j; for (i = 0; i < n; ++i) { for (j = 0; j < n; ++j) scanf("%d", &x[i][j]); } } // 函数定义 // 功能: 输出一个n*n的矩阵x void output(int x[][N], int n) { int i, j; for (i = 0; i < n; ++i) { for (j = 0; j < n; ++j) printf("%4d", x[i][j]); printf("\n"); } } // 函数rotate_to_right定义 // 功能: 把一个n*n的矩阵x,每一列向右移, 最右边一列绕回左边 // 待补足 void rotate_to_right(int x[][N], int n) { int temp; for (int i = 0; i < n; i++) { temp = x[i][n - 1]; for (int j = n - 1; j > 0; j--) { x[i][j] = x[i][j - 1]; } x[i][0] = temp; } }
实验结果:
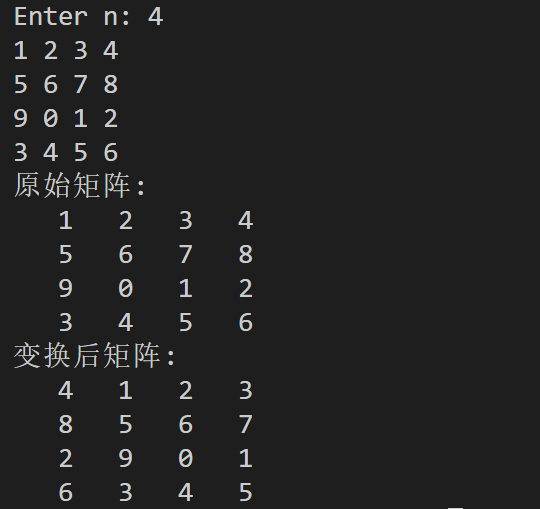
任务六:
#include <stdio.h> #define N 100 void dec_to_n(int x, int n); // 函数声明 int main() { int x; while (printf("输入十进制整数: "), scanf("%d", &x) != EOF) { dec_to_n(x, 2); // 函数调用: 把x转换成二进制输出 dec_to_n(x, 8); // 函数调用: 把x转换成八进制输出 dec_to_n(x, 16); // 函数调用: 把x转换成十六进制输出 printf("\n"); } return 0; } // 函数定义 // 功能: 把十进制数x转换成n进制,打印输出 void dec_to_n(int x, int n) { char digits[] = "0123456789ABCDEF"; char result[N]; int index = 0; if (x == 0) { printf("0"); return; } int isNegative = 0; if (x < 0) { isNegative = 1; x = -x; // 转换为正数处理 } while (x > 0) { int remainder = x % n; result[index++] = digits[remainder]; x = x / n; } if (isNegative) { printf("-"); } for (int i = index - 1; i >= 0; i--) { printf("%c", result[i]); } printf("\n"); }
实验结果:
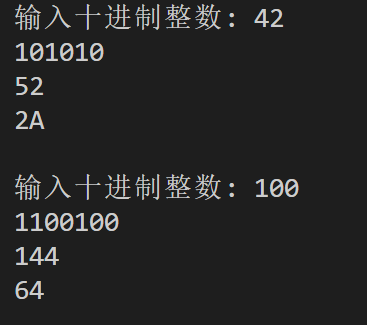
任务七:
#include <stdio.h> #define N 100 // 函数声明 void input(int x[][N], int n); void output(int x[][N], int n); int is_magic(int x[][N], int n); int main() { int n; int x[N][N]; while (printf("输入n: "), scanf("%d", &n) != EOF) { printf("输入方阵:\n"); input(x, n); printf("输出方阵:\n"); output(x, n); if (is_magic(x, n)) { printf("是魔方矩阵\n\n"); } else { printf("不是魔方矩阵\n\n"); } } return 0; } void input(int x[][N], int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { scanf("%d", &x[i][j]); } } } void output(int x[][N], int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { printf("%4d", x[i][j]); } printf("\n"); } } // 功能: 判断一个n阶方阵是否为魔方矩阵,如果是,返回1,否则,返回0 int is_magic(int x[][N], int n) { // 检查是否包含1到n²的所有整数 int expected_sum = 0; int actual_sum = 0; int found[N * N + 1] = {0}; // 标记数组,记录数字是否出现 // 计算1到n²的和 for (int i = 1; i <= n * n; i++) { expected_sum += i; } // 检查矩阵中的数字 for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { int num = x[i][j]; // 检查数字是否在1到n²范围内 if (num < 1 || num > n * n) { return 0; } // 检查数字是否重复 if (found[num]) { return 0; } found[num] = 1; actual_sum += num; } } // 检查数字总和是否正确 if (actual_sum != expected_sum) { return 0; } // 计算第一行的和作为标准值 int standard_sum = 0; for (int j = 0; j < n; j++) { standard_sum += x[0][j]; } // 检查所有行的和 for (int i = 0; i < n; i++) { int row_sum = 0; for (int j = 0; j < n; j++) { row_sum += x[i][j]; } if (row_sum != standard_sum) { return 0; } } // 检查所有列的和 for (int j = 0; j < n; j++) { int col_sum = 0; for (int i = 0; i < n; i++) { col_sum += x[i][j]; } if (col_sum != standard_sum) { return 0; } } // 检查主对角线 int diag1_sum = 0; for (int i = 0; i < n; i++) { diag1_sum += x[i][i]; } if (diag1_sum != standard_sum) { return 0; } // 检查副对角线 int diag2_sum = 0; for (int i = 0; i < n; i++) { diag2_sum += x[i][n - 1 - i]; } if (diag2_sum != standard_sum) { return 0; } return 1; }
实验结果:
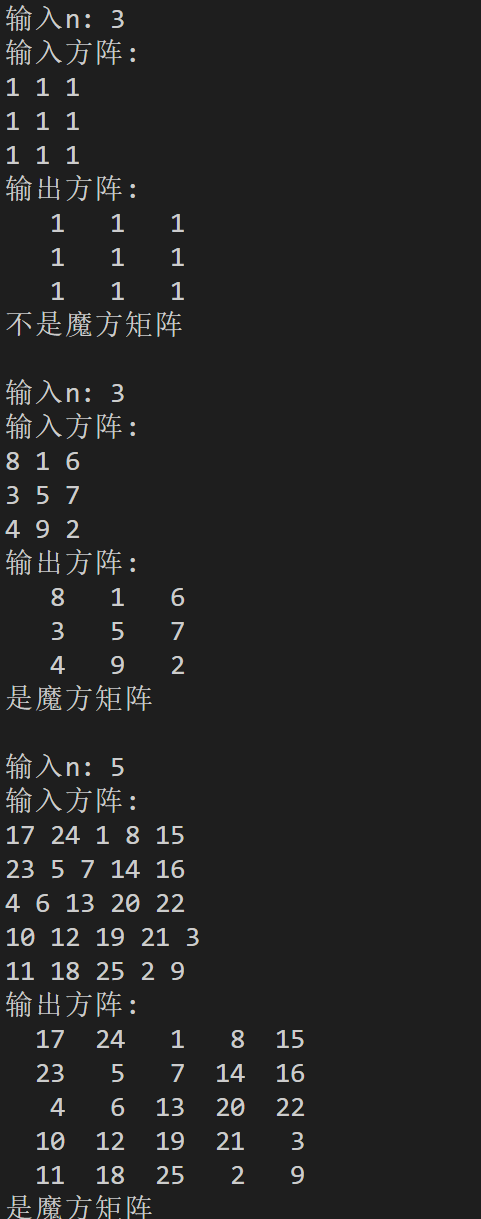
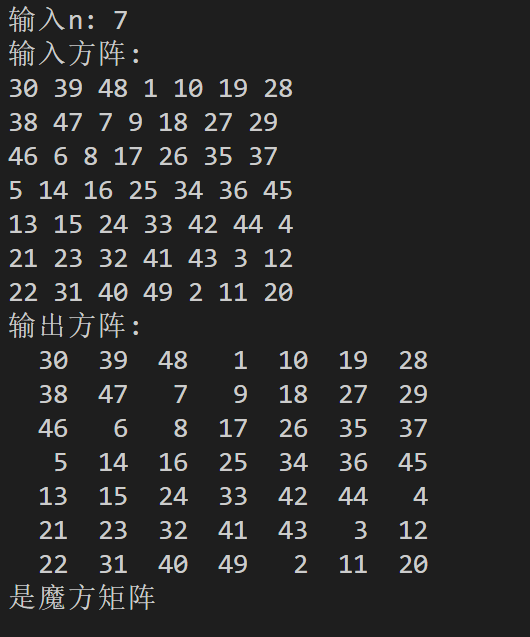



 浙公网安备 33010602011771号
浙公网安备 33010602011771号