Floyd

另一个求解最短路径的经典算法是Floyd,时间复杂度为O(n^3)，所以如果只求一个点到另一个点的最短路径，应该用Dijkstra算法，时间复杂度为O(n^2)。如果要求全部的最短路径，还是推荐Floyd,因为代码更简单，更整洁：

核心代码

主要就是通过简单的思路，如果借由中间节点的路径要小于直达的费用，那么就替换中间节点为路径中间量

if(D[i][j] > D[i][k]+D[k][j])
    D[i][j] = D[i][k] + D[k][j];

全部代码

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #define MAXSIZE 9
 4 #define INF 65535
 5 int num[MAXSIZE][MAXSIZE] = {
 6      0,    1,  5,INF,INF,INF,INF,INF,INF,
 7      1,    0,  3,  7,  5,INF,INF,INF,INF,
 8      5,    3,  0,INF,  1,  7,INF,INF,INF,
 9      INF,  7,INF,  0,  2,INF,  3,INF,INF,
10      INF,  5,  1,  2,  0,  3,  6,  9,INF,
11      INF,INF,  7,INF,  3,  0,INF,  5,INF,
12      INF,INF,INF,  3,  6,INF,  0,  2,  7,
13      INF,INF,INF,INF,  9,  5,  2,  0,  4,
14      INF,INF,INF,INF,INF,INF,  7,  4,  0
15 };
16 void getPath(int begin,int end,int D[][9],int P[][9]);
17 void printDP(int D[][9],int P[][9]);
18 int main(){
19     int D[MAXSIZE][MAXSIZE];
20     int P[MAXSIZE][MAXSIZE];
21     //initializtion
22     int i,j,k;
23     for(i=0;    i<MAXSIZE;i++){
24         for(j=0;j<MAXSIZE;j++){
25             D[i][j] = num[i][j];
26             P[i][j] = j;
27         }
28     }
29     printDP(D,P);
30     
31     //finding
32     for(k=0;k<MAXSIZE;k++){
33         for(i=0;i<MAXSIZE;i++){
34             for(j=0;j<MAXSIZE;j++){
35                 if(D[i][j] > D[i][k]+D[k][j]){
36                     D[i][j] = D[i][k] + D[k][j];
37                     P[i][j] = P[i][k];
38                 }
39             }
40         }
41     }
42     printDP(D,P);
43 
44     getPath(0,8,D,P);
45     getchar();
46     return 0;
47 }
48 void printDP(int D[][9],int P[][9]){
49 /*    可以用二维数组名作为实参或者形参，在被调用函数中对形参数组定义时可以可以指定所有维数的大小，
50     也可以省略第一维的大小说明。如：
51     void Func(int array[3][10]);
52     void Func(int array[][10]);
53     */
54     int i,j;
55     for(i=0;i<MAXSIZE;i++){
56         for(j=0;j<MAXSIZE;j++){
57             printf("%d ",D[i][j]);
58         }
59         printf("\n");
60     }
61     printf("\n");
62     for(i=0;i<MAXSIZE;i++){
63         for(j=0;j<MAXSIZE;j++){
64             printf("%d ",P[i][j]);
65         }
66         printf("\n");
67     }
68     printf("--------------------------------------------------------------\n");
69 }
70 void getPath(int begin,int end,int D[][9],int P[][9]){
71     int target = begin;
72     printf("%d",target);
73     int sum = 0;
74     while(target != end){
75         target = P[target][end];
76         sum += D[target][end];
77         printf("->%d(%d)",target,D[target][end]);
78     }
79     printf("\n%d",sum);
80 }

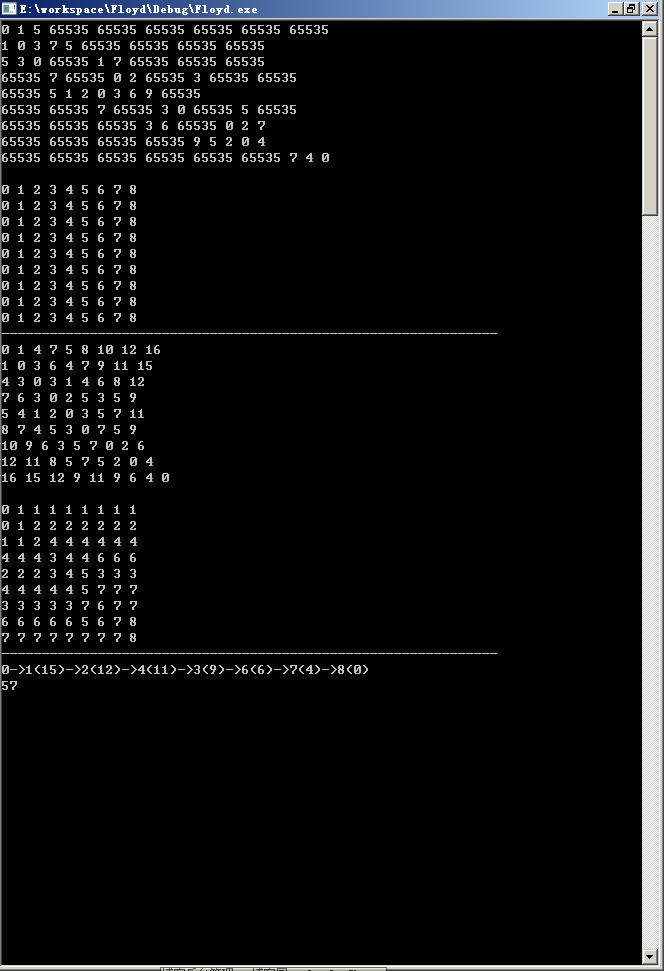
运行示例

posted @ 2014-03-19 16:35  xingoo  阅读(523)  评论(0)  编辑  收藏  举报