结对编程
[结对编程作业--天津地铁线路]
一、任务:
实现一个帮助进行地铁出行路线规划的命令行程序。
二、设计信息
- 开发语言:JAVA
- 算法:Dijkstra
三、需求分析及实现
-
需求1
-
在程序启动时,自动获取到地图信息
需要实现一个支持自动加载subway.txt 文件的程序,程序启动时需要通过读取 -map 参数来获得对应的自定义地铁文件(命名为 subway.txt),从而得到地铁线路图的信息。一个调用应用程序的示例如下:
java subway -map subway.txt
-
需求2
-
查询指定地铁线经过的站点
在应用程序上,需要支持一个新的命令行参数 -a ,指定用户希望查询的地铁线路。
在给定地铁线路时,程序需要从线路的起始站点开始,依次输出该地铁线经过的所有站点,直到终点站。输出的文件使用
-o参数来指定。一个调用应用程序的示例如下:java subway -a 1号线 -map subway.txt -o station.txt下为实际输出的station.txt 文件的内容
地铁:1号线 刘园 西横堤 果酒厂 本溪路 勤俭道 洪湖里 西站 西北角 西南角 二纬路 海光寺 鞍山道 营口道 小白楼 下瓦房 南楼 土城 陈塘庄 复兴门 华山里 财经大学 双林 李楼 -
需求3
-
计算从出发到目的站点之间的最短路线并输出经过的站点的个数和路径
如果用户希望坐地铁,他希望能通过最少的站数从出发点到达目的地,这样就可以在命令行中以 -b 参数加两个地铁站点名称分别作为出发与目的,比如用户希望知道 洪湖里 到复兴路 之间的最短路线是怎样的,他就可以使用如下命令让程序将结果写入 routine.txt 中。
subway.exe -b 洪湖里 复兴路 -map subway.txt -o routine.txt
程序将计算从出发到目的站点之间的最短(经过的站点数最少)路线,并输出经过的站点的个数和路径(包括出发与目的站点)。如果需要换乘,会在换乘站的下一行输出换乘的线路。输出的文件使用-o参数来指定。
一个调用应用程序的示例如下:
java subway -b 华苑 乐园道 -map subway.txt -o routine.txt
下为实际输出的routine.txt 文件的内容
起始站:华苑
3号线
王顶堤
红旗南路
6号线
迎风道
南翠屏
水上公园东路
肿瘤医院
天津宾馆
文化中心
乐园道
四、实现过程
-
功能函数
// 加载地铁线路数据public void loadLineFile(String strSubwayFileName)
// 地铁数据处理void parseSubwayStationsData()
// 最优路径规划Path Dijkstra(String strStartStationName, String strEndStationName)
// 打印一个路径void printPath(String start,String end, String strOutFileName)
// 获取特定地铁线路数据void printLineInfo(String LineName, String strOutFile)
-
部分函数展示
// 最优路径规划 <迪杰斯特拉算法>
Path Dijkstra(String strStartStationName, String strEndStationName) {
// todo: 进行一些合法性检查
Station stationStart = mapNametoStation.get(strStartStationName);
Station stationEnd = mapNametoStation.get(strEndStationName);
if(stationStart==null || stationEnd==null)
{
System.out.println("起始站或终点输入不正确,请检查输入数据!");
return null;
}
mapTransferStationNametoDistance.put(strEndStationName, nMaxDistance);
mapTransferStationNametoDistance.put(strStartStationName, nMaxDistance);
Path pathStart = new Path();
pathStart.nFDistance = 0;
pathStart.stationLastStationInPath = stationStart;
Path Dijkstra = new Path();
Dijkstra.nFDistance = nMaxDistance;
Stack<Path> stackAllPaths = new Stack<>();
stackAllPaths.push(pathStart);
Set<String> TStationNameSet = new TreeSet<>();
for(String strname: mapTransferStationNametoDistance.keySet()) {
TStationNameSet.add(strname);
}
for(String strname: mapTransferStationNametoDistance.keySet()) {
finalMap.put(strname,"null");
}
while (!stackAllPaths.empty()) {
Path pathCurrent = stackAllPaths.pop();
if (pathCurrent.nFDistance > Dijkstra.nFDistance) {
continue;
}
int nBDistance = getStationsDistance(pathCurrent.stationLastStationInPath, stationEnd);
if (nBDistance == 0) { // 到达终止节点
if (pathCurrent.nFDistance < Dijkstra.nFDistance) {
Dijkstra = pathCurrent;
}
continue;
}
int minDistance = 1000000;
String nextStation = null;
TStationNameSet.remove(pathCurrent.stationLastStationInPath.stationName);
for (String strTStationName: mapTransferStationNametoDistance.keySet()) {
Station stationTransfer = mapNametoStation.get(strTStationName);
int nDistanceDelta = getStationsDistance(pathCurrent.stationLastStationInPath, stationTransfer);
int nTStationDistance = pathCurrent.nFDistance + nDistanceDelta;
if (nTStationDistance >= mapTransferStationNametoDistance.get(strTStationName)) {
continue;
}
finalMap.put(strTStationName,pathCurrent.stationLastStationInPath.stationName);
mapTransferStationNametoDistance.put(strTStationName, nTStationDistance);
}
for(String strTStationName: mapTransferStationNametoDistance.keySet()) {
int Distance = mapTransferStationNametoDistance.get(strTStationName);
if(Distance<minDistance&& TStationNameSet.contains(strTStationName)) {
minDistance = Distance;
nextStation = strTStationName;
}
}
Station stationTransfer = mapNametoStation.get(nextStation);
Path pathNew = new Path();
pathNew.nFDistance = minDistance;
pathNew.stationLastStationInPath = stationTransfer;
stackAllPaths.push(pathNew);
}
// System.out.println(finalMap);
return Dijkstra;
}
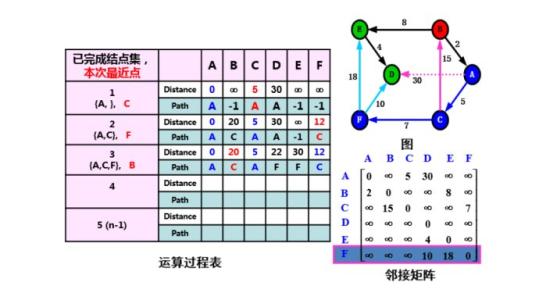
迪杰斯特拉算法求最短路径
-
算法思想
G={V,E}
- 初始时令 S={V0},T=V-S={其余顶点},T中顶点对应的距离值
若存在<V0,Vi>,d(V0,Vi)为<V0,Vi>弧上的权值
若不存在<V0,Vi>,d(V0,Vi)为∞
-
从T中选取一个与S中顶点有关联边且权值最小的顶点W,加入到S中
-
对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值
重复上述步骤2、3,直到S中包含峙所有顶点,即W=Vi为止
-
算法图解
五、测试
- 1.读取subway中的线路信息
java subway -map subway.txt

- 2.查寻指定地铁线经过的站点
java subway -a 2号线 -map subway.txt -o station.txt
输出的station.txt文件内容:
地铁:2号线
曹庄
卞兴
芥园西道
咸阳路
长虹公园
广开四马路
西南角
鼓楼
东南角
建国道
天津站
远洋国际中心
顺驰桥
靖江路
翠阜新村
屿东城
登州路
国山路
空港经济区
滨海国际机场
- 3.查询的到达重点的路径***
java subway -b 刘园 鼓楼 -map subway.txt -o routine.txt
输出的routine.txt文件内容:
地铁:1号线
西横堤
果酒厂
本溪路
勤俭道
洪湖里
西站
西北角
西南角
地铁:2号线
鼓楼
- 4.终点的站点不存在**
java subway -b 刘园 卫星广场 -map subway.txt -o routine.txt

- 5.查询不存在的地铁线路
java subway -a 8号线 -map subway.txt -o station.txt

六、项目完成时间统计
| PSP 2.1 | Personal Software Process Stages | Time |
|---|---|---|
| Planning | 计划 | |
| · Estimate | · 估计这个任务需要多少时间 | 3weeks |
| Development | 开发 | |
| · Analysis | · 需求分析 (包括学习新技术) | 2days |
| · Design Spec | · 生成设计文档 | 2days |
| · Design Review | · 设计复审 (和同事审核设计文档) | 1day |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 2day |
| · Design | · 具体设计 | 3days |
| · Coding | · 具体编码 | 5days |
| · Code Review | · 代码复审 | 1days |
| · Test | · 测试(自我测试,修改代码,提交修改) | 1day |
| Reporting | 报告 | |
| · Test Report | · 测试报告 | 1day |
| · Size Measurement | · 计算工作量 | 1day |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 1days |
| 合计 | 20days |
七.总结
在本次天津地铁路径的规划中,主要是用缔结斯塔拉这个单源最短路径求解的算法进行实现的,在项目进行中也遇到了许许多多的问题,主要的原因是对JAVA语言的不熟悉,俩个人之间第一次做结对项目的不适应,还好最后都在有效的沟通下解决了这些问题,进而实现了这次的结对编程作业。
总之,通过本次项目实验,让我们俩体会到了作为一个程序员,一个人单打独斗是不可以的,要互帮互助,及时沟通,才能更好更快的完成项目。
github代码地址:https://github.com/xiehong/work/invitations


 浙公网安备 33010602011771号
浙公网安备 33010602011771号