树
树的定义
专业定义
- 有且只有一个称为根的节点
- 有若干个互不相干的子树,这些子树本身也是一棵树
通俗的定义
- 树是由节点和边组成
- 每一个节点只能有一个父节点,但可以有多个子节点
- 但有一个节点例外,该节点没有父节点,此节点称为根节点
专业术语
- 节点:树的节点包含一个数据元素及若干个指向其子树的分支
- 父节点:有子树的结点是其子树的根节点的父结点
- 子节点:若A结点是B结点的父结点,则称B结点是A结点的子结点
- 子孙:某一结点的子树中的所有结点是这个结点的子孙
- 堂兄弟:其双亲在同一层的节点护卫堂兄弟
- 深度:从根节点到最底层节点的层数称为深度(根节点是一棵树第一层)
- 叶子节点:没有子节点的节点
- 非终端节点:实际上就是非叶子节点,即有子节点的节点
- 节点的度:节点的子树个数
- 树的度:树的所有节点中最大的度数
树的分类
一般树
- 任意一个子节点的节点的个数都部收限制
二叉树
- 二叉树定义
- 任意一个节点的子节点的个数最多两个,且子节点的位置不可更改(二叉树为有序树)
- 二叉树性质
- 在二叉树的第 \(i\) 层上之多有 \(2^{i-1}\) 个节点
- 深度为 \(k\) 的二叉树至多有 \(2^k-1\) 个节点(\(k\geq1\))
- 对任意一课二叉树 \(T\) ,如果其终端节点树为 \(n_0\) ,度为 2 的节点数为 \(n_2\) ,则 \(n_0=n_2+1\)
- 具有 \(n\) 个节点的完全二叉树的深度为 \(\lfloor log_2n\rfloor+1\)( \(\lfloor x \rfloor\) 表示不大于 \(x\) 的最大整数,反之, \(\lceil x \rceil\) 表示不小于 \(x\) 的最小整数 )
- 如果对一颗有 \(n\) 个节点的完全二叉树(其深度为 \(\lfloor log_2n\rfloor+1\) )的节点按层序编号(从第 1 层到 \(\lfloor log_2n\rfloor+1\) 层,每层从做导游),则对任一节点 \(i\) (\(1\leq i \leq n\)),有:
- 如果\(i=1\) ,则节点 \(i\) 是二叉树的根,无双亲;如果 \(i>1\) ,则其双亲 \(PARENT(i)\) 是节点 \(\lfloor i/2 \rfloor\).
- 如果 \(2i>n\) ,则节点 \(i\) 无左孩子(节点 \(i\) 为叶子节点);否则其左孩子 \(LCHILD(i)\) 是节点 \(2i\)
- 如果 \(2i+1>n\) ,则节点 \(i\) 无又孩子;否则其右孩子 \(RCHILDE(i)\) 是节点 \(2i+1\) 。
- 二叉树分类
-
一般二叉树
-
满二叉树
-
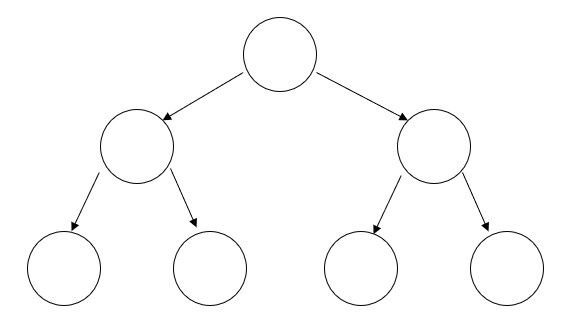
一棵深度为 \(k\) 且有 \(2^k-1\) 个节点的二叉树称为满而二叉树,这种树的特点是每一层上的节点数都是最大节点数(通俗定义:在不增加树的层数的前提下,无法再多添加一个节点的二叉树就是满二叉树)
-
图示:
-
-
完全二叉树(满二叉树是完全二叉树的一个特例)
-
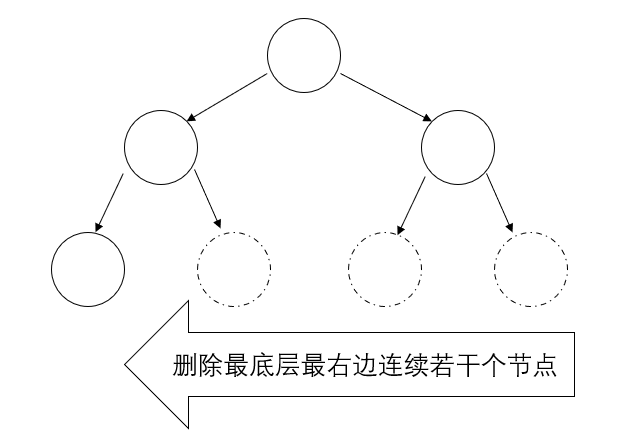
深度为 \(k\) 的,有 \(n\) 个节点的二叉树,当且仅当其每一个节点都与深度为 \(k\) 的满二叉树中编号从 1 至 \(n\) 的节点一一对应,称之为完全二叉树 (通俗定义:如果只是删除了满二叉树最底层最右边的连续若干个节点,这样形成的二叉树就是完全二叉树)
-
图示:
-
-
森林
- n 个互不相交的树的集合
树的存储
二叉树的存储
- 连续存储(以数组的形式存储)(完全二叉树)
- 连续存储要求这个树必须是完全二叉树,所以在存储普通二叉树的时候要把普通二叉树添加元素成为完全二叉树
- 有三种算法:先序遍历,中序遍历,后序遍历。这三种算法都可以将非线性的树转换成线性的结构来保存,这三种算法对同一个树形成的线性结构的元素顺序是不同的,但是相同的是:它们都要求所存储的树是完全二叉树,只有这样才能在由线性结构转化为原来的二叉树是有一定的公式可以套用。否则不能由转化而来的线性结构反推原来的二叉树。——具体看后文先序中序后序遍历。
- 连续存储使用完全二叉树的优点
- 知道节点的个数可以立即得到又几层
- 已知任何一个节点,可以立即得到其父节点,子节点,有无子节点
- 连续存储使用完全二叉树的缺点
- 耗用内存空间过大
- 连续存储要求这个树必须是完全二叉树,所以在存储普通二叉树的时候要把普通二叉树添加元素成为完全二叉树
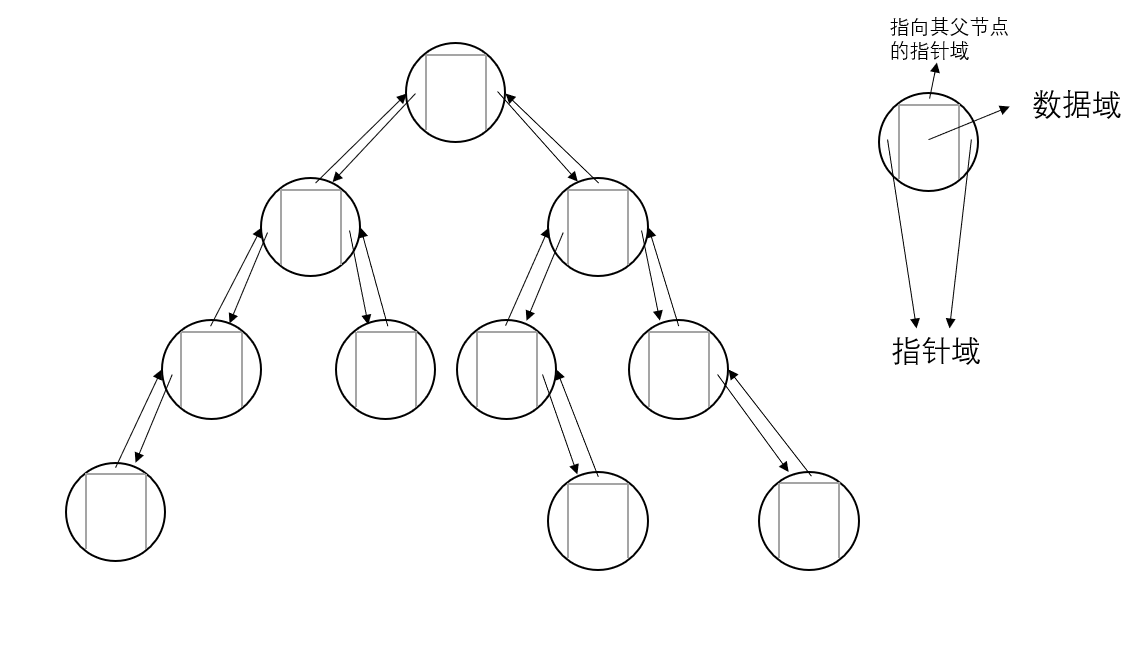
- 链式存储
- 图示:
-
第一种(不容易寻找一个节点的父节点

-
第二种(较为容易寻找一个节点的父节点)
-
- 图示:
一般树的存储
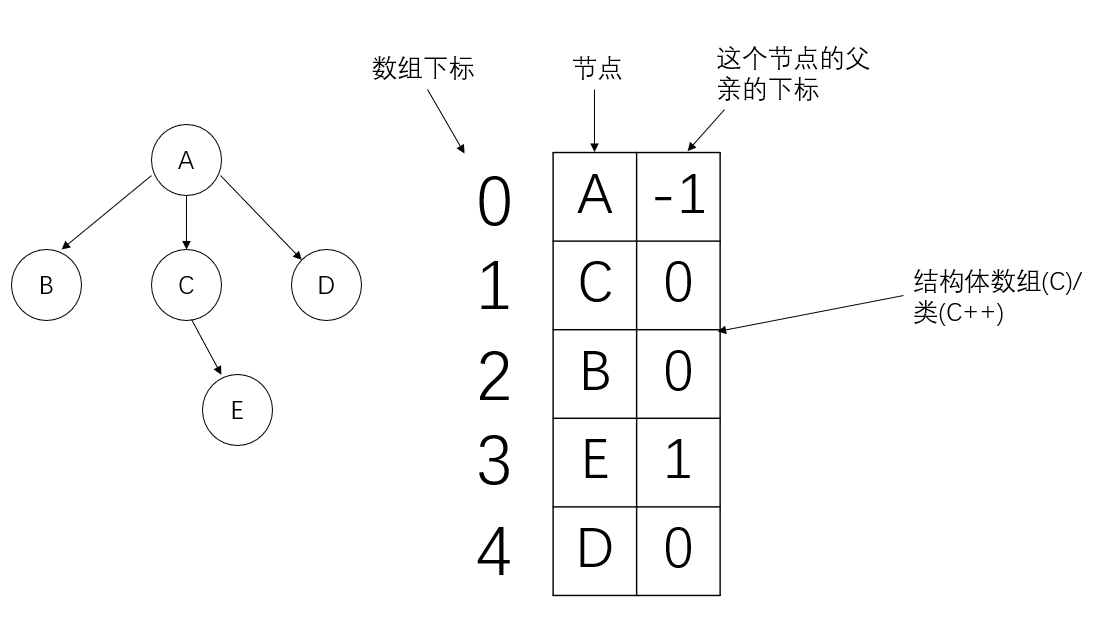
- 双亲表示法
-
图示:( \(A\) 没有父节点,所以也就没有父节点下标,所以用 \(-1\)表示)
-
优点:寻找父节点很方便
-
缺点:寻找子节点不方便
-
- 孩子表示法
-
图示:
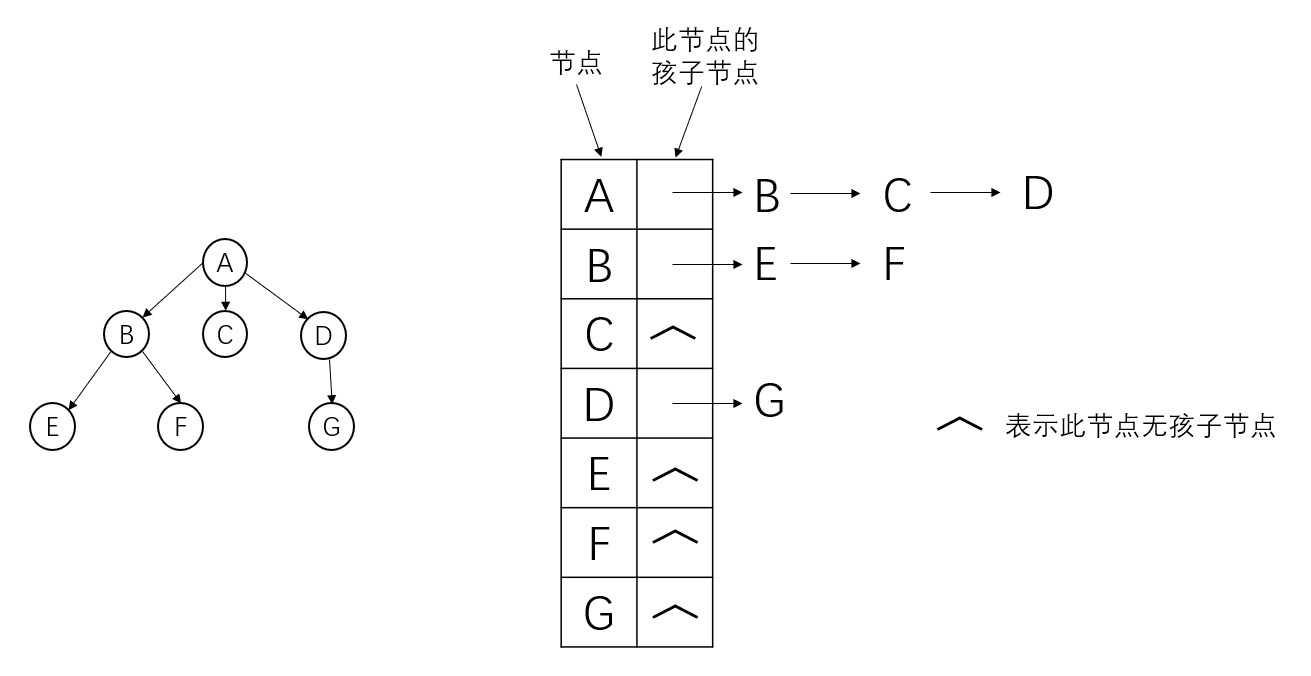
-
优点:寻找子节点很方便
-
缺点:寻找父节点不方便
-
- 双亲孩子表示法
-
图示:

-
优点:求父节点和子节点都很方便
-
- 二叉树表示法(把一个普通树转化为二叉树来存储)
-
普通树转化为二叉树方法:设法保证任意一个节点的左指针域指向它的第一个孩子,右边的指针域指向它的兄弟节点
-
一棵普通的树,转化为二叉树,转化后的二叉树一定没有右子树(见下图转化后节点 \(1\) )
-
图示:
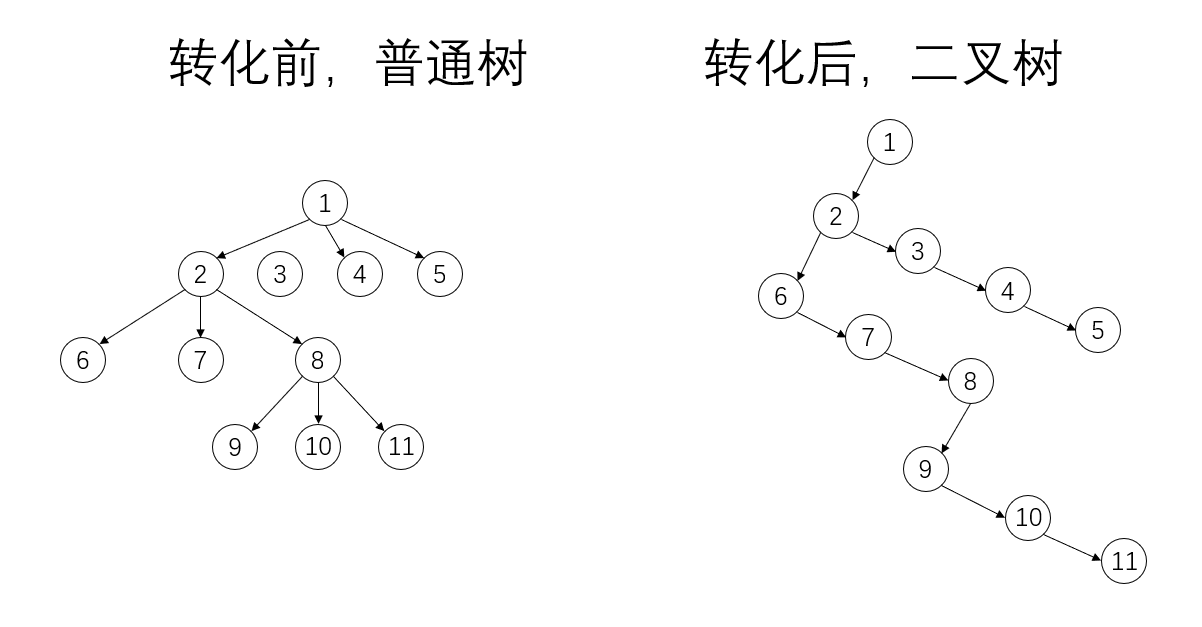
-
森林的存储(类似于普通树转换为二叉树存贮)
-
森林转化为二叉树的方法:把需要存储的几棵树的根节点当作兄弟,以后的操作和普通树转化为二叉树相同
-
图示:
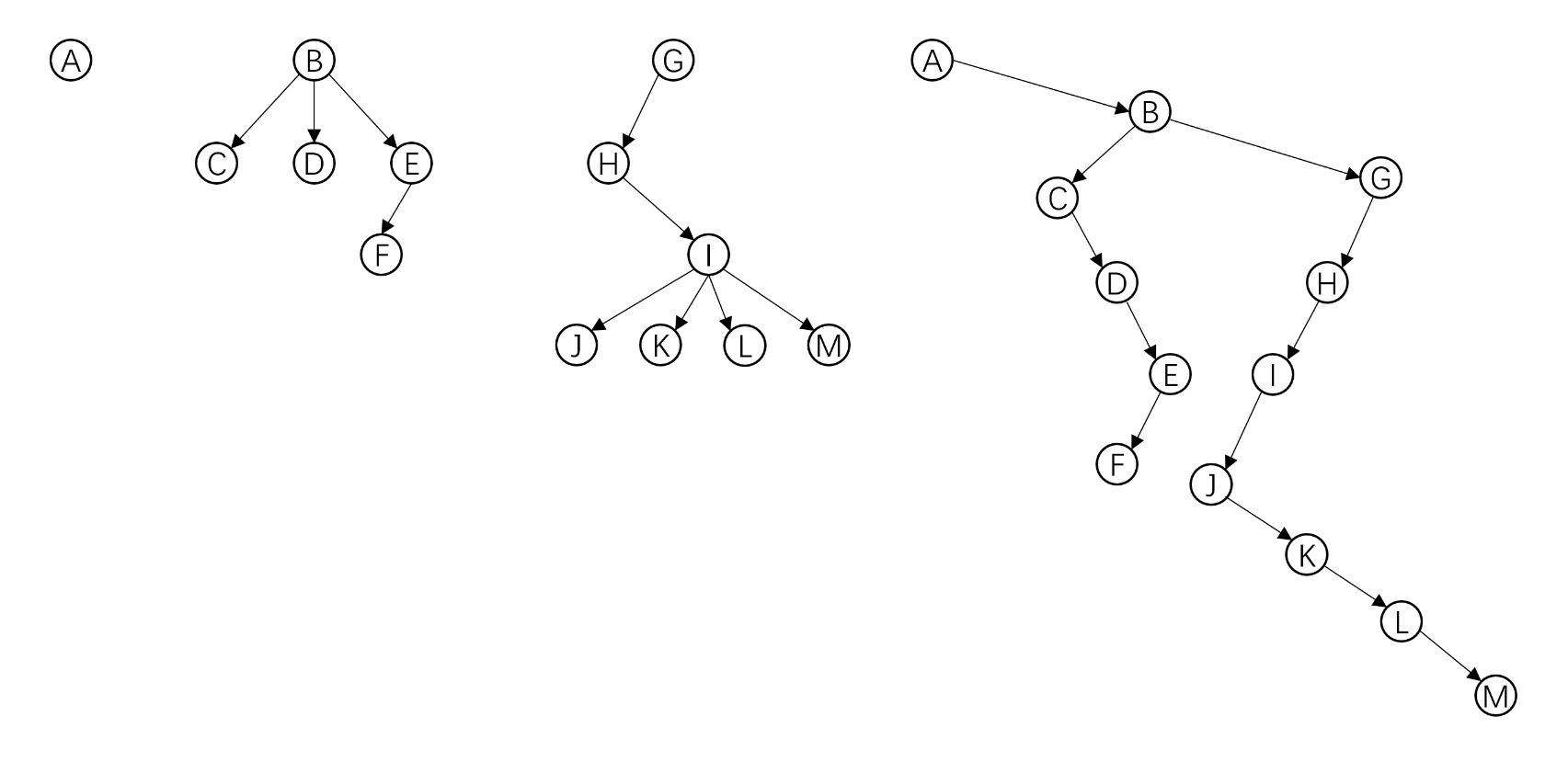
树的操作(二叉树的操作)
遍历
-
先序遍历(先访问根节点)
-
描述:
- 先访问根节点
- 再先序访问左子树
- 再先序访问右子树
-
详细描述(结合下图):先访问根节点 \(A\) ,再先序访问 \(A\) 的左子树,要先序访问A的左子树,只要先序访问 \(A\) 的左子树的根节点,即 \(B\) ,再先序访问 \(B\) 的左子树,要先序访问 \(B\) 的左子树,只要先序访问 \(B\) 的左子树的根节点,即 \(D\) ,再先序访问 \(D\) 的左子树,因为 \(D\) 没有左子树,所以先序访问 \(D\) 的右子树,因为 \(D\) 没有右子树,所以先序访问 \(D\) 完成,所以先序访问 \(B\) 的左子树完成,再先序访问 \(B\) 的右子树,因为 \(B\) 没有右子树,所以先序访问 \(B\) 完成,所以先序访问 \(A\) 的左子树完成,再先序访问 \(A\) 的右子树,要先序访问 \(A\) 的右子树,只要先序访问 \(A\) 的右子树的根节点,即 \(C\) ,再先序访问 \(C\) 的左子树,要先序访问 \(C\) 的左子树,只要先序访问 \(C\) 的左子树的根节点,即 \(E\) ,再先序访问 \(E\) 的左子树,因为 \(E\) 没有左子树,所以先序访问 \(E\) 的右子树,因为 \(E\) 没有右子树,所以先序访问 \(E\) 完成,所以先序访问 \(C\) 的左子树完成,再先序访问 \(C\) 的右子树,要先序访问 \(C\) 的右子树,只要先序访问 \(C\) 的右子树的根节点,即 \(F\) ,再先序访问 \(F\) 的左子树,要先序访问 \(F\) 的左子树,只要先序访问 \(F\) 的左子树的根节点,即 \(G\) ,再先序访问 \(G\) 的左子树,因为 \(G\) 没有左子树,所以先序访问 \(G\) 的右子树,因为 \(G\) 没有右子树,所以先序访问 \(G\) 完成,所以先序访问 \(F\) 的左子树完成,再先序访问 \(F\) 的右子树,因为 \(F\) 没有右子树,所以先序访问 \(F\) 完成,所以先序访问 \(C\) 的右子树完成,所以先序访问 \(A\) 的右子树完成,所以先序遍历完成(这就是递归遍历,参照前面的递归专题更好理解)
-
图示:
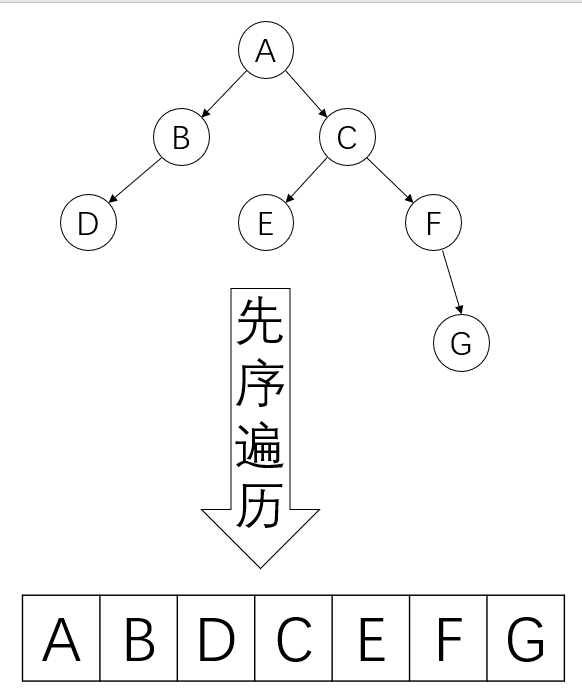
-
-
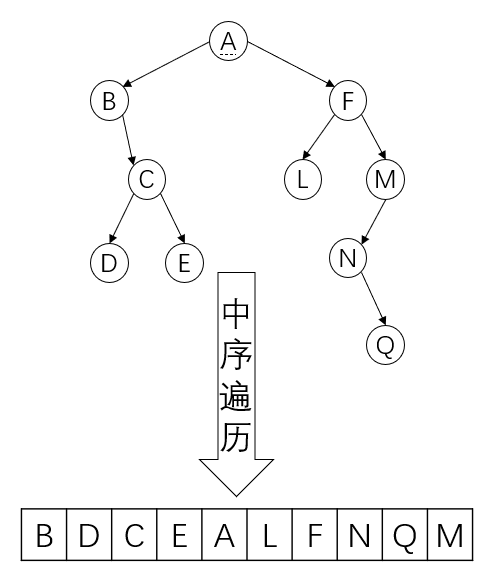
中序遍历(中间访问根节点)
-
描述:
- 先中序遍历左子树
- 再访问根节点
- 再中序遍历右子树
-
具体描述(结合下图):先中序访问 \(A\) 的左子树,要中序访问 \(A\) 的左子树,就要中序访问 \(B\) 的左子树,因为 \(B\) 没有左子树,所以再中序访问 \(B\) 节点,再中序访问 \(B\) 的右子树,要中序访问 \(B\) 的右子树,就要中序访问 \(C\) 的左子树,要中序访问 \(C\) 的左子树,就要中序访问 \(D\) 的左子树,因为 \(D\) 没有左子树,所以再中序访问 \(D\) 节点,再中序访问 \(D\) 的右子树,因为 \(D\) 没有右子树,所以中序访问 \(D\) 完成,所以中序访问 \(C\) 的左子树完成,所以再中序访问 \(C\) 节点,再中序访问 \(C\) 的右子树,要中序访问 \(C\) 的右子树,就要中序访问 \(E\) 的左子树,因为 \(E\) 没有左子树,所以再访问 \(E\) 节点,再中序访问 \(E\) 的右子树,因为 \(E\) 没有右子树,所以中序访问 \(E\) 完成,所以中序访问 \(C\) 的右子树完成,所以中序访问 \(C\) 完成,所以中序访问 \(B\) 的右子树完成,所以中序访问 \(B\) 完成,所以中序访问 \(A\) 的左子树完成,再中序访问 \(A\) 节点,再中序访问 \(A\) 的右子树,要中序访问 \(A\) 的右子树,就要中序访问 \(F\) 的左子树,要中序访问 \(F\) 的左子树,就要中序访问 \(L\) 的左子树,因为 \(L\) 没有左子树,所以再中序访问 \(L\) 节点,再中序访问 \(F\) 的右子树,要中序访问 \(F\) 的右子树,就要中序访问 \(M\) 的左子树,要中序访问 \(M\) 的左子树,就要中序访问 \(N\) 的左子树,因为 \(N\) 没有左子树,所以中序访问 \(N\) 节点,再中序访问 \(N\) 的右子树,要中序访问 \(N\) 的右子树,就要中序访问 \(Q\) 的左子树,因为 \(Q\) 没有左子树,所以中序访问 \(Q\) 节点,再中序访问 \(Q\) 的右子树,因为 \(Q\) 没有右子树,所以中序访问 \(Q\) 完成,所以中序访问 \(N\) 的右子树完成,所以中序访问 \(N\) 完成,所以中序访问 \(M\) 的左子树完成,所以再中序访问 \(M\) 节点,再中序访问 \(M\) 的右子树,因为 \(M\) 没有右子树,所以中序访问 \(M\) 的右子树完成,所以中序访问 \(M\) 完成,所以中序访问 \(F\) 的右子树完成,所以中序访问 \(F\) 完成,所以中序访问 \(A\) 的右子树完成,所以中序访问 \(A\) 完成。
-
图示:
-
-
后序遍历(最后访问根节点)
- 描述:
- 后序遍历左子树
- 后序遍历右子树
- 再访后序问根节点
- 具体描述:和前两个相差不大,可以自己推出来
- 描述:
已知两种遍历序列求原始二叉树
-
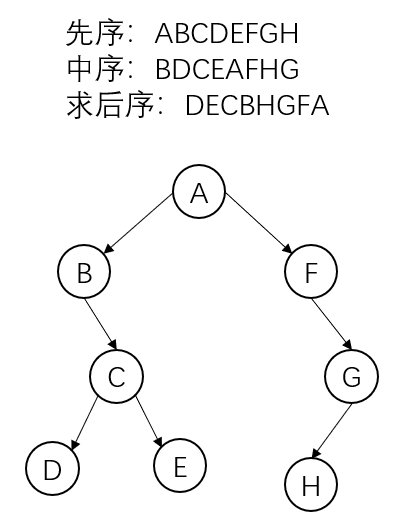
已知先序和中序求后序:
- 例:
-
先序:ABCDEFGH
-
后序:BDCEAFHG
-
求后序:DECBHGFA
-
详解:因为先序是先遍历根节点再遍历左子树在遍历右子树,且先序中最先出现 \(A\) ,所以 \(A\) 是整个二叉树的根节点,再看中序,因为中序是先遍历左子树再遍历根节点再遍历右子树,所以根节点左侧的一定是它的左子树,右边一定是它的右子树,所以 \(A\) 的左子树包含 \(B\) \(D\) \(C\) \(E\) 这四个节点,再看先序, \(B\) \(D\) \(C\) \(E\) 中\(B\) 先出现,所以 \(B\) 是 \(A\) 的左子树的根节点,再看中序,由于 \(B\) 左侧没有元素,所以 \(B\) 只有右子树,它的右子树包含 \(D\) \(C\) \(E\) 这三个节点,再看先序, \(D\) \(C\) \(E\) 中\(C\) 先出现,所以 \(C\) 是 \(B\) 的右子树的根节点,再看中序, \(C\) 左右各有一个元素,分别为 \(D\) , \(E\) ,所以 \(C\) 有左子树和右子树,且左子树为元素 \(D\) ,右子树为元素 \(E\) ,至此, \(A\) 的左子树确定完毕,再看 \(A\) 的右子树,先看中序, \(A\) 的右边有 \(F\) \(H\) \(G\) ,所以 \(A\) 的右子树包含 \(F\) \(G\) \(H\) 这三个节点,再看先序,由于\(F\) \(G\) \(H\) 中\(F\) 先出现,所以 \(F\) 为 \(A\) 的右子树的根节点,再看中序,由于 \(F\) 左侧没有元素,所以 \(F\) 只有右子树,且右子树包含 \(H\) \(G\) 这两个元素,再看先序,由于\(H\) \(G\) 中 \(G\) 先出点,所以 \(G\) 为 \(F\) 右子树的根节点,再看中序, \(G\) 只有左边有且只有元素 \(H\) ,所以 \(G\) 只有左子树,且为 \(H\) ,至此, \(A\) 的右子树确定完毕。然后即可得出后序。
-
- 例:
-
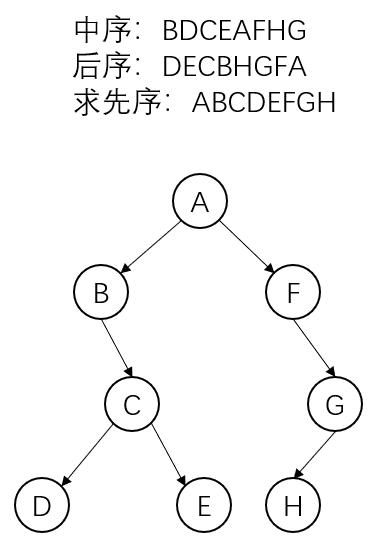
已知中序和后序求先序
- 例:
-
中序:BDCEAFHG
-
后序:DECBHGFA
-
求先序:ABCDEFGH
-
详解:因为后序是先遍历左子树在遍历右子树在遍历根节点,且后序中最后出现的是 \(A\) ,所以 \(A\) 为根节点,再看中序,因为 \(A\) 左侧为 \(B\) \(D\) \(C\) \(E\) ,所以 \(A\) 的左子树有 \(B\) \(D\) \(C\) \(E\) 这四个元素,再看后序,因为 \(B\) \(D\) \(C\) \(E\) 中 \(B\) 最后出现,所以 \(B\) 是 \(A\) 的左子树的根节点,再看中序,由于 \(B\) 只有右侧有元素,所以 \(B\) 没有左子树,且右子树包含 \(D\) \(C\) \(E\) 这三个元素,再看后序,由于 \(D\) \(C\) \(E\) 中 \(C\) 最后出现,所以 \(C\) 是 \(B\) 的右子树的根节点,再看中序,由于 \(C\) 左右各有一个元素,分别为 \(D\) , \(E\) ,所以 \(C\) 的左子树为元素 \(D\) ,右子树为元素 \(E\) ,至此, \(A\) 的左子树确定完成,再看右子树,先看中序,由于 \(A\) 右侧有 \(F\) \(H\) \(G\)这三个元素,所以 \(A\) 的右子树包含 \(F\) \(H\) \(G\)这三个元素,再看后序,由于 \(F\) \(H\) \(G\)中 \(F\) 最后出现,所以 \(F\) 是 \(A\) 的右子树的根节点,再看中序,由于 \(F\) 只有右侧有元素,所以 \(F\) 没有左子树,且右子树包含 \(H\) \(G\),再看后序,由于 \(H\) \(G\)中 \(G\)做后出现,所以 \(G\)是 \(F\) 的右子树的根节点,再看中序, \(G\)有且只有左侧有元素 \(H\),所以 \(G\)只有左子树 \(H\),没有右子树,至此, \(A\) 的右子树确定完毕。然后即可得出后序。
-
- 例:
-
注意:已知先序和后序是不可以推出原始二叉树的,只有先序和中序,或者后序和中序才可以(必须有中序参与)唯一的确定一个二叉树
树的应用
- 树是数据库中数据组织的一种重要形式
- 操作系统子父进程的关系本身就是一棵树
- 面向对象语言中类的继承关系本身就是一棵树
- 赫夫曼树
遍历程序演示
#include <stdio.h>
#include <stdlib.h>
typedef struct BTNode{
char data;
struct BTNode *pLchild;
struct BTNode *pRchild;
}BTNODE,*PBTNODE;
PBTNODE CreatBTree(void);
void PreTraverseBtree(PBTNODE pT);//先序
void InTraverseBTree(PBTNODE pT);//中序
void PostTraverseBTree(PBTNODE pT);//后序
int main()
{
PBTNODE pT=CreatBTree();
printf("先序:");
PreTraverseBtree(pT);//先序
printf("\n");
printf("中序:");
InTraverseBTree(pT);//中序
printf("\n");
printf("后序:");
PostTraverseBTree(pT);//后序
return 0;
}
PBTNODE CreatBTree(void)
{
PBTNODE pA=(PBTNODE)malloc(sizeof(BTNODE));
PBTNODE pB=(PBTNODE)malloc(sizeof(BTNODE));
PBTNODE pC=(PBTNODE)malloc(sizeof(BTNODE));
PBTNODE pD=(PBTNODE)malloc(sizeof(BTNODE));
PBTNODE pE=(PBTNODE)malloc(sizeof(BTNODE));
pA->data='A';
pB->data='B';
pC->data='C';
pD->data='D';
pE->data='E';
pA->pLchild=pB;
pA->pRchild=pC;
pB->pLchild=pB->pRchild=NULL;
pC->pLchild=pD;
pC->pRchild=NULL;
pD->pLchild=NULL;
pD->pRchild=pE;
pE->pLchild=pE->pRchild=NULL;
return pA;
}
void PreTraverseBtree(PBTNODE pT)
{
if(pT!=NULL){
printf("%c ",pT->data);
if(pT->pLchild!=NULL){
PreTraverseBtree(pT->pLchild);
}
if(pT->pRchild!=NULL){
PreTraverseBtree(pT->pRchild);
}
}
}
void InTraverseBTree(PBTNODE pT){
if(pT!=NULL){
if(pT->pLchild!=NULL){
InTraverseBTree(pT->pLchild);
}
printf("%c ",pT->data);
if(pT->pRchild!=NULL){
InTraverseBTree(pT->pRchild);
}
}
}
void PostTraverseBTree(PBTNODE pT){
if(pT!=NULL){
if(pT->pLchild!=NULL){
PostTraverseBTree(pT->pLchild);
}
if(pT->pRchild!=NULL){
PostTraverseBTree(pT->pRchild);
}
printf("%c ",pT->data);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号